Scalable Multi-Objective and Meta Reinforcement Learning via Gradient Estimation

We study the problem of efficiently estimating policies that simultaneously optimize multiple objectives in reinforcement learning (RL). Given $n$ objectives (or tasks), we seek the optimal partition of these objectives into $k \ll n$ groups, where each group comprises related objectives that can be trained together. This problem arises in applications such as robotics, control, and preference optimization in language models, where learning a single policy for all $n$ objectives is suboptimal as $n$ grows. We introduce a two-stage procedure -- meta-training followed by fine-tuning -- to address this problem. We first learn a meta-policy for all objectives using multitask learning. Then, we adapt the meta-policy to multiple randomly sampled subsets of objectives. The adaptation step leverages a first-order approximation property of well-trained policy networks, which is empirically verified to be accurate within a $2\%$ error margin across various RL environments. The resulting algorithm, PolicyGradEx, efficiently estimates an aggregate task-affinity score matrix given a policy evaluation algorithm. Based on the estimated affinity score matrix, we cluster the $n$ objectives into $k$ groups by maximizing the intra-cluster affinity scores. Experiments on three robotic control and the Meta-World benchmarks demonstrate that our approach outperforms state-of-the-art baselines by $16\%$ on average, while delivering up to $26\times$ faster speedup relative to performing full training to obtain the clusters. Ablation studies validate each component of our approach. For instance, compared with random grouping and gradient-similarity-based grouping, our loss-based clustering yields an improvement of $19\%$. Finally, we analyze the generalization error of policy networks by measuring the Hessian trace of the loss surface, which gives non-vacuous measures relative to the observed generalization errors.

Back to Bayesics: Uncovering Human Mobility Distributions and Anomalies with an Integrated Statistical and Neural Framework

Existing methods for anomaly detection often fall short due to their inability to handle the complexity, heterogeneity, and high dimensionality inherent in real-world mobility data. In this paper, we propose DeepBayesic, a novel framework that integrates Bayesian principles with deep neural networks to model the underlying multivariate distributions from sparse and complex datasets. Unlike traditional models, DeepBayesic is designed to manage heterogeneous inputs, accommodating both continuous and categorical data to provide a more comprehensive understanding of mobility patterns. The framework features customized neural density estimators and hybrid architectures, allowing for flexibility in modeling diverse feature distributions and enabling the use of specialized neural networks tailored to different data types. Our approach also leverages agent embeddings for personalized anomaly detection, enhancing its ability to distinguish between normal and anomalous behaviors for individual agents. We evaluate our approach on several mobility datasets, demonstrating significant improvements over state-of-the-art anomaly detection methods. Our results indicate that incorporating personalization and advanced sequence modeling techniques can substantially enhance the ability to detect subtle and complex anomalies in spatiotemporal event sequences.

C-SURE: Shrinkage Estimator and Prototype Classifier for Complex-Valued Deep Learning

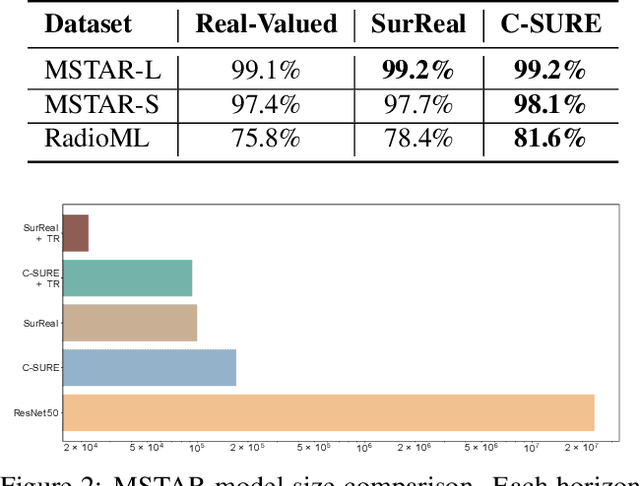
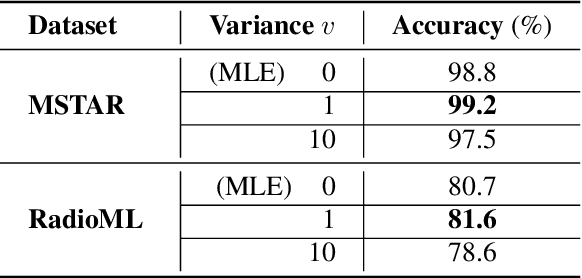
The James-Stein (JS) shrinkage estimator is a biased estimator that captures the mean of Gaussian random vectors.While it has a desirable statistical property of dominance over the maximum likelihood estimator (MLE) in terms of mean squared error (MSE), not much progress has been made on extending the estimator onto manifold-valued data. We propose C-SURE, a novel Stein's unbiased risk estimate (SURE) of the JS estimator on the manifold of complex-valued data with a theoretically proven optimum over MLE. Adapting the architecture of the complex-valued SurReal classifier, we further incorporate C-SURE into a prototype convolutional neural network (CNN) classifier. We compare C-SURE with SurReal and a real-valued baseline on complex-valued MSTAR and RadioML datasets. C-SURE is more accurate and robust than SurReal, and the shrinkage estimator is always better than MLE for the same prototype classifier. Like SurReal, C-SURE is much smaller, outperforming the real-valued baseline on MSTAR (RadioML) with less than 1 percent (3 percent) of the baseline size