Reinforcement Learning vs. Distillation: Understanding Accuracy and Capability in LLM Reasoning

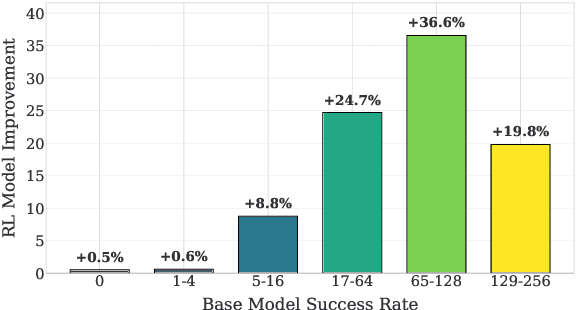
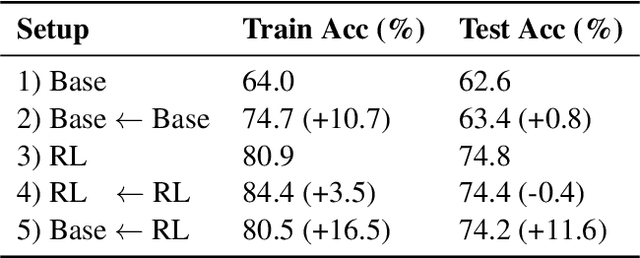
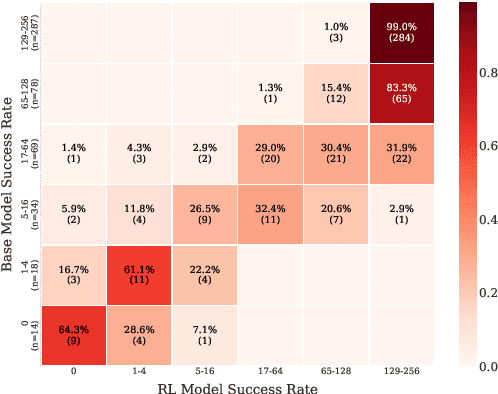
Recent studies have shown that reinforcement learning with verifiable rewards (RLVR) enhances overall accuracy but fails to improve capability, while distillation can improve both. In this paper, we investigate the mechanisms behind these phenomena. First, we demonstrate that RLVR does not improve capability because it focuses on improving the accuracy of the less-difficult questions to the detriment of the accuracy of the most difficult questions, thereby leading to no improvement in capability. Second, we find that RLVR does not merely increase the success probability for the less difficult questions, but in our small model settings produces quality responses that were absent in its output distribution before training. In addition, we show these responses are neither noticeably longer nor feature more reflection-related keywords, underscoring the need for more reliable indicators of response quality. Third, we show that while distillation reliably improves accuracy by learning strong reasoning patterns, it only improves capability when new knowledge is introduced. Moreover, when distilling only with reasoning patterns and no new knowledge, the accuracy of the less-difficult questions improves to the detriment of the most difficult questions, similar to RLVR. Together, these findings offer a clearer understanding of how RLVR and distillation shape reasoning behavior in language models.

Warm Up Before You Train: Unlocking General Reasoning in Resource-Constrained Settings

Designing effective reasoning-capable LLMs typically requires training using Reinforcement Learning with Verifiable Rewards (RLVR) or distillation with carefully curated Long Chain of Thoughts (CoT), both of which depend heavily on extensive training data. This creates a major challenge when the amount of quality training data is scarce. We propose a sample-efficient, two-stage training strategy to develop reasoning LLMs under limited supervision. In the first stage, we "warm up" the model by distilling Long CoTs from a toy domain, namely, Knights \& Knaves (K\&K) logic puzzles to acquire general reasoning skills. In the second stage, we apply RLVR to the warmed-up model using a limited set of target-domain examples. Our experiments demonstrate that this two-phase approach offers several benefits: $(i)$ the warmup phase alone facilitates generalized reasoning, leading to performance improvements across a range of tasks, including MATH, HumanEval$^{+}$, and MMLU-Pro. $(ii)$ When both the base model and the warmed-up model are RLVR trained on the same small dataset ($\leq100$ examples), the warmed-up model consistently outperforms the base model; $(iii)$ Warming up before RLVR training allows a model to maintain cross-domain generalizability even after training on a specific domain; $(iv)$ Introducing warmup in the pipeline improves not only accuracy but also overall sample efficiency during RLVR training. The results in this paper highlight the promise of warmup for building robust reasoning LLMs in data-scarce environments.

Mathematical Reasoning in Large Language Models: Assessing Logical and Arithmetic Errors across Wide Numerical Ranges

Mathematical reasoning in Large Language Models (LLMs) is often evaluated using benchmarks with limited numerical ranges, failing to reflect real-world problem-solving across diverse scales. Furthermore, most existing evaluation methods only compare model outputs to ground-truth answers, obscuring insights into reasoning processes. To address these limitations, we introduce GSM-Ranges, a dataset generator derived from GSM8K that systematically perturbs numerical values in math problems to assess model robustness across varying numerical scales. Additionally, we propose a novel grading methodology that distinguishes between logical and non-logical errors, offering a more precise evaluation of reasoning processes beyond computational accuracy. Our experiments with various models reveal a significant increase in logical error rates-up to 14 percentage points-as numerical complexity rises, demonstrating a general weakness in reasoning with out-of-distribution numerical values. Moreover, while models demonstrate high accuracy on standalone arithmetic tasks, their performance deteriorates substantially when computations are embedded within word problems. These findings provide a comprehensive evaluation of LLMs' mathematical reasoning capabilities and inform future research directions for improving numerical generalization in language models.