Sequential Gaussian Variational Inference for Nonlinear State Estimation applied to Robotic Applications

Probabilistic state estimation is essential for robots navigating uncertain environments. Accurately and efficiently managing uncertainty in estimated states is key to robust robotic operation. However, nonlinearities in robotic platforms pose significant challenges that require advanced estimation techniques. Gaussian variational inference (GVI) offers an optimization perspective on the estimation problem, providing analytically tractable solutions and efficiencies derived from the geometry of Gaussian space. We propose a Sequential Gaussian Variational Inference (S-GVI) method to address nonlinearity and provide efficient sequential inference processes. Our approach integrates sequential Bayesian principles into the GVI framework, which are addressed using statistical approximations and gradient updates on the information geometry. Validations through simulations and real-world experiments demonstrate significant improvements in state estimation over the Maximum A Posteriori (MAP) estimation method.

Stein-MAP: A Sequential Variational Inference Framework for Maximum A Posteriori Estimation

State estimation poses substantial challenges in robotics, often involving encounters with multimodality in real-world scenarios. To address these challenges, it is essential to calculate Maximum a posteriori (MAP) sequences from joint probability distributions of latent states and observations over time. However, it generally involves a trade-off between approximation errors and computational complexity. In this article, we propose a new method for MAP sequence estimation called Stein-MAP, which effectively manages multimodality with fewer approximation errors while significantly reducing computational and memory burdens. Our key contribution lies in the introduction of a sequential variational inference framework designed to handle temporal dependencies among transition states within dynamical system models. The framework integrates Stein's identity from probability theory and reproducing kernel Hilbert space (RKHS) theory, enabling computationally efficient MAP sequence estimation. As a MAP sequence estimator, Stein-MAP boasts a computational complexity of O(N), where N is the number of particles, in contrast to the O(N^2) complexity of the Viterbi algorithm. The proposed method is empirically validated through real-world experiments focused on range-only (wireless) localization. The results demonstrate a substantial enhancement in state estimation compared to existing methods. A remarkable feature of Stein-MAP is that it can attain improved state estimation with only 40 to 50 particles, as opposed to the 1000 particles that the particle filter or its variants require.

Bayesian Learning for Dynamic Target Localization with Human-provided Spatial Information

This paper considers a human-autonomy collaborative sensor data fusion for dynamic target localization in a Bayesian framework. To compensate for the shortcomings of an autonomous tracking system, we propose to collect spatial sensing information from human operators who visually monitor the target and can provide target localization information in the form of free sketches encircling the area where the target is located. Our focus in this paper is to construct an adaptive probabilistic model for human-provided inputs where the adaption terms capture the level of reliability of the human inputs. The next contribution of this paper is a novel joint Bayesian learning method to fuse human and autonomous sensor inputs in a manner that the dynamic changes in human detection reliability are also captured and accounted for. A unique aspect of this Bayesian modeling framework is its analytical closed-form update equations, endowing our method with significant computational efficiency. Simulations demonstrate our results.

Online Target Localization using Adaptive Belief Propagation in the HMM Framework

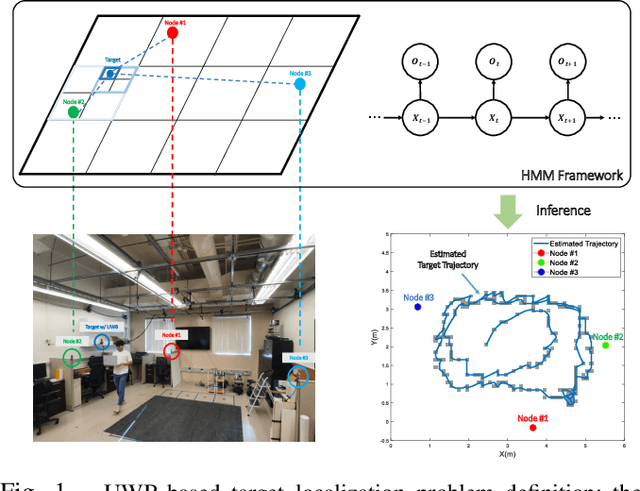
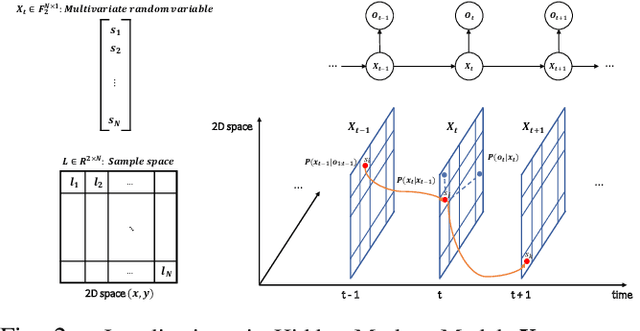
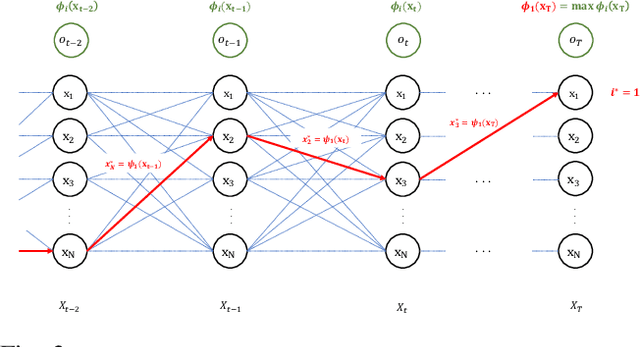
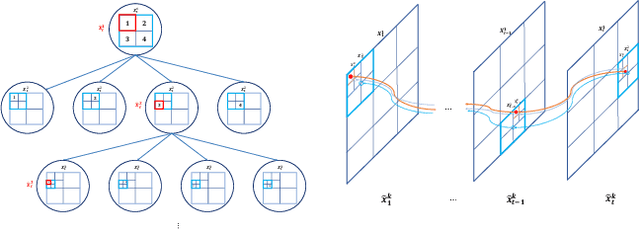
This paper proposes a novel adaptive sample space-based Viterbi algorithm for ultra-wideband (UWB) based target localization in an online manner. As the discretized area of interest is defined as a finite number of hidden states, the most probable trajectory of the unspecified agent is computed efficiently via dynamic programming in a Hidden Markov Model (HMM) framework. Furthermore, the approach has no requirements about Gaussian assumption and linearization for Bayesian calculation. However, the issue of computational complexity becomes very critical as the number of hidden states increases for estimation accuracy and large space. Previous localization works, based on discrete-state HMM, handle a small number of hidden variables, which represent specific paths or places. Inspired by the k-d Tree algorithm (e.g., quadtree) that is commonly used in the computer vision field, we propose a belief propagation in the most probable belief space with a low to high-resolution sequentially, thus reducing the required resources significantly. Our method has three advantages for localization: (a) no Gaussian assumptions and linearization, (b) handling the whole area of interest, not specific or small map representations, (c) reducing computation time and required memory size. Experimental tests demonstrate our results.