Equivariant Representations for Non-Free Group Actions

We introduce a method for learning representations that are equivariant with respect to general group actions over data. Differently from existing equivariant representation learners, our method is suitable for actions that are not free i.e., that stabilize data via nontrivial symmetries. Our method is grounded in the orbit-stabilizer theorem from group theory, which guarantees that an ideal learner infers an isomorphic representation. Finally, we provide an empirical investigation on image datasets with rotational symmetries and show that taking stabilizers into account improves the quality of the representations.

Quantifying and Learning Disentangled Representations with Limited Supervision

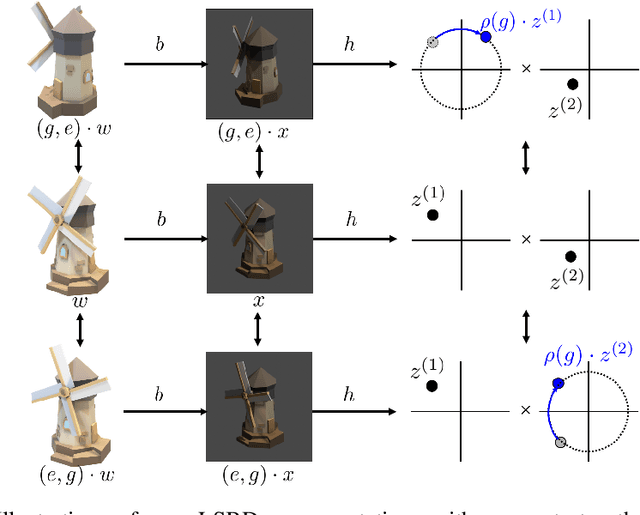
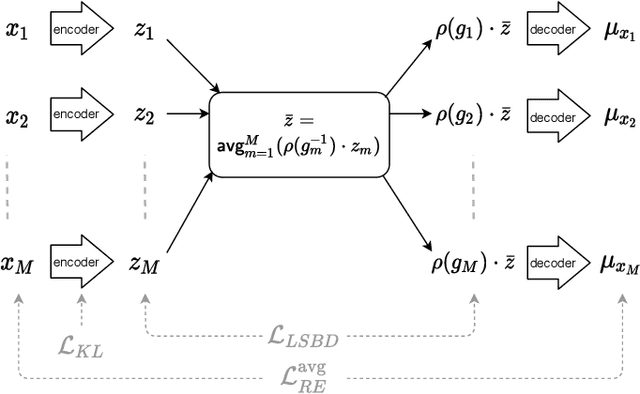
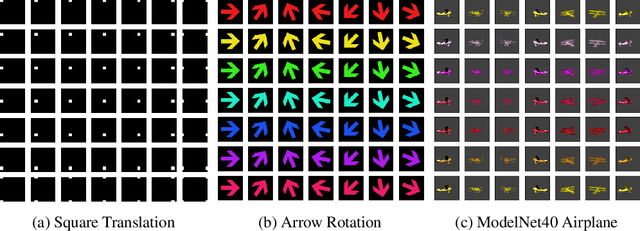
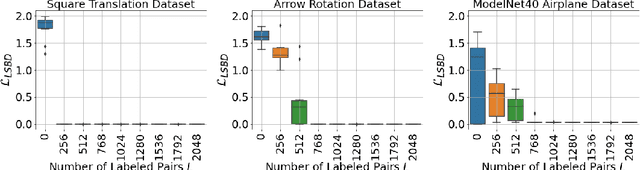
Learning low-dimensional representations that disentangle the underlying factors of variation in data has been posited as an important step towards interpretable machine learning with good generalization. To address the fact that there is no consensus on what disentanglement entails, Higgins et al. (2018) propose a formal definition for Linear Symmetry-Based Disentanglement, or LSBD, arguing that underlying real-world transformations give exploitable structure to data. Although several works focus on learning LSBD representations, such methods require supervision on the underlying transformations for the entire dataset, and cannot deal with unlabeled data. Moreover, none of these works provide a metric to quantify LSBD. We propose a metric to quantify LSBD representations that is easy to compute under certain well-defined assumptions. Furthermore, we present a method that can leverage unlabeled data, such that LSBD representations can be learned with limited supervision on transformations. Using our LSBD metric, our results show that limited supervision is indeed sufficient to learn LSBD representations.

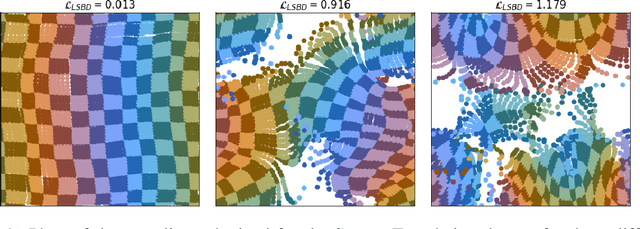
A Metric for Linear Symmetry-Based Disentanglement

The definition of Linear Symmetry-Based Disentanglement (LSBD) proposed by (Higgins et al., 2018) outlines the properties that should characterize a disentangled representation that captures the symmetries of data. However, it is not clear how to measure the degree to which a data representation fulfills these properties. We propose a metric for the evaluation of the level of LSBD that a data representation achieves. We provide a practical method to evaluate this metric and use it to evaluate the disentanglement of the data representations obtained for three datasets with underlying $SO(2)$ symmetries.

Complex Vehicle Routing with Memory Augmented Neural Networks

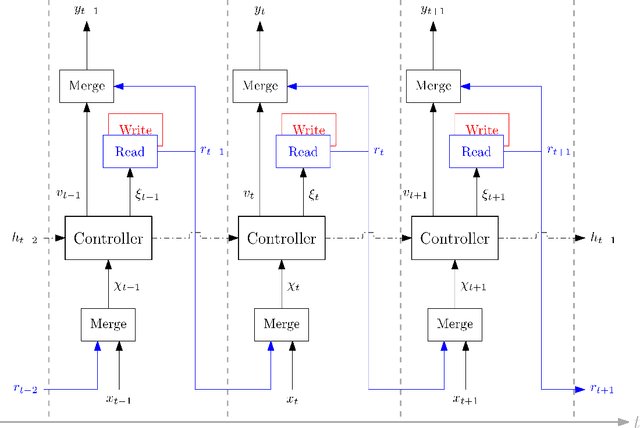
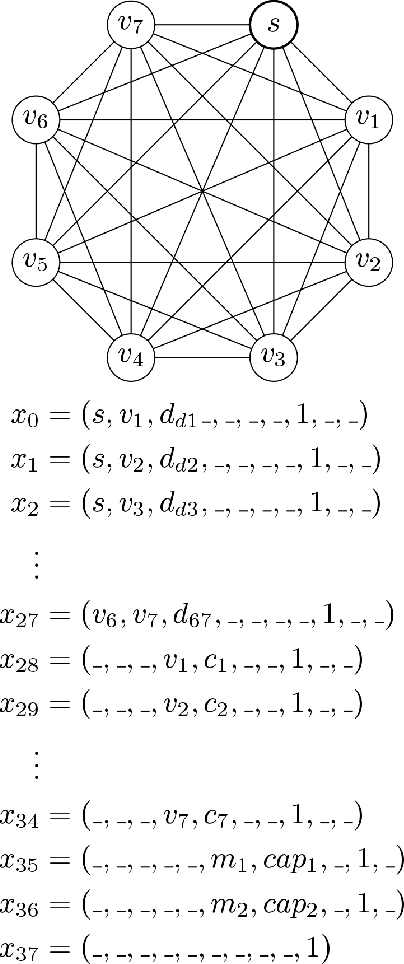
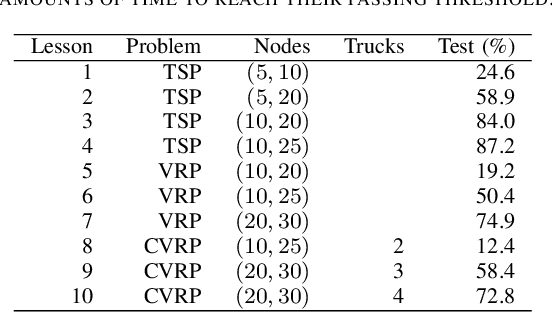
Complex real-life routing challenges can be modeled as variations of well-known combinatorial optimization problems. These routing problems have long been studied and are difficult to solve at scale. The particular setting may also make exact formulation difficult. Deep Learning offers an increasingly attractive alternative to traditional solutions, which mainly revolve around the use of various heuristics. Deep Learning may provide solutions which are less time-consuming and of higher quality at large scales, as it generally does not need to generate solutions in an iterative manner, and Deep Learning models have shown a surprising capacity for solving complex tasks in recent years. Here we consider a particular variation of the Capacitated Vehicle Routing (CVRP) problem and investigate the use of Deep Learning models with explicit memory components. Such memory components may help in gaining insight into the model's decisions as the memory and operations on it can be directly inspected at any time, and may assist in scaling the method to such a size that it becomes viable for industry settings.