A finite-sample generalization bound for stable LPV systems

One of the main theoretical challenges in learning dynamical systems from data is providing upper bounds on the generalization error, that is, the difference between the expected prediction error and the empirical prediction error measured on some finite sample. In machine learning, a popular class of such bounds are the so-called Probably Approximately Correct (PAC) bounds. In this paper, we derive a PAC bound for stable continuous-time linear parameter-varying (LPV) systems. Our bound depends on the H2 norm of the chosen class of the LPV systems, but does not depend on the time interval for which the signals are considered.

PAC-Bayes Generalisation Bounds for Dynamical Systems Including Stable RNNs

In this paper, we derive a PAC-Bayes bound on the generalisation gap, in a supervised time-series setting for a special class of discrete-time non-linear dynamical systems. This class includes stable recurrent neural networks (RNN), and the motivation for this work was its application to RNNs. In order to achieve the results, we impose some stability constraints, on the allowed models. Here, stability is understood in the sense of dynamical systems. For RNNs, these stability conditions can be expressed in terms of conditions on the weights. We assume the processes involved are essentially bounded and the loss functions are Lipschitz. The proposed bound on the generalisation gap depends on the mixing coefficient of the data distribution, and the essential supremum of the data. Furthermore, the bound converges to zero as the dataset size increases. In this paper, we 1) formalize the learning problem, 2) derive a PAC-Bayesian error bound for such systems, 3) discuss various consequences of this error bound, and 4) show an illustrative example, with discussions on computing the proposed bound. Unlike other available bounds the derived bound holds for non i.i.d. data (time-series) and it does not grow with the number of steps of the RNN.

PAC-Bayesian bounds for learning LTI-ss systems with input from empirical loss

In this paper we derive a Probably Approxilmately Correct(PAC)-Bayesian error bound for linear time-invariant (LTI) stochastic dynamical systems with inputs. Such bounds are widespread in machine learning, and they are useful for characterizing the predictive power of models learned from finitely many data points. In particular, with the bound derived in this paper relates future average prediction errors with the prediction error generated by the model on the data used for learning. In turn, this allows us to provide finite-sample error bounds for a wide class of learning/system identification algorithms. Furthermore, as LTI systems are a sub-class of recurrent neural networks (RNNs), these error bounds could be a first step towards PAC-Bayesian bounds for RNNs.

PAC-Bayesian-Like Error Bound for a Class of Linear Time-Invariant Stochastic State-Space Models

In this paper we derive a PAC-Bayesian-Like error bound for a class of stochastic dynamical systems with inputs, namely, for linear time-invariant stochastic state-space models (stochastic LTI systems for short). This class of systems is widely used in control engineering and econometrics, in particular, they represent a special case of recurrent neural networks. In this paper we 1) formalize the learning problem for stochastic LTI systems with inputs, 2) derive a PAC-Bayesian-Like error bound for such systems, 3) discuss various consequences of this error bound.

Noisy Learning for Neural ODEs Acts as a Robustness Locus Widening

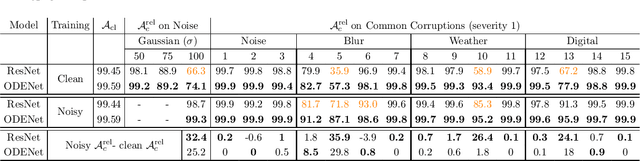
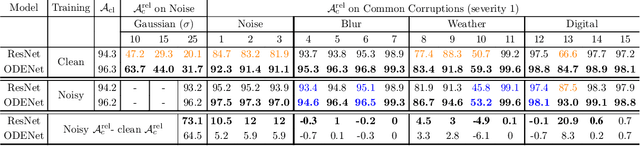
We investigate the problems and challenges of evaluating the robustness of Differential Equation-based (DE) networks against synthetic distribution shifts. We propose a novel and simple accuracy metric which can be used to evaluate intrinsic robustness and to validate dataset corruption simulators. We also propose methodology recommendations, destined for evaluating the many faces of neural DEs' robustness and for comparing them with their discrete counterparts rigorously. We then use this criteria to evaluate a cheap data augmentation technique as a reliable way for demonstrating the natural robustness of neural ODEs against simulated image corruptions across multiple datasets.

Realization Theory Of Recurrent Neural ODEs Using Polynomial System Embeddings

In this paper we show that neural ODE analogs of recurrent (ODE-RNN) and Long Short-Term Memory (ODE-LSTM) networks can be algorithmically embeddeded into the class of polynomial systems. This embedding preserves input-output behavior and can suitably be extended to other neural DE architectures. We then use realization theory of polynomial systems to provide necessary conditions for an input-output map to be realizable by an ODE-LSTM and sufficient conditions for minimality of such systems. These results represent the first steps towards realization theory of recurrent neural ODE architectures, which is is expected be useful for model reduction and learning algorithm analysis of recurrent neural ODEs.

Optimal Prediction of Unmeasured Output from Measurable Outputs In LTI Systems

In this short article, we showcase the derivation of an optimal predictor, when one part of system's output is not measured but is able to be predicted from the rest of the system's output which is measured. According to author's knowledge, similar derivations have been done before but not in state-space representation.

PAC-Bayesian theory for stochastic LTI systems

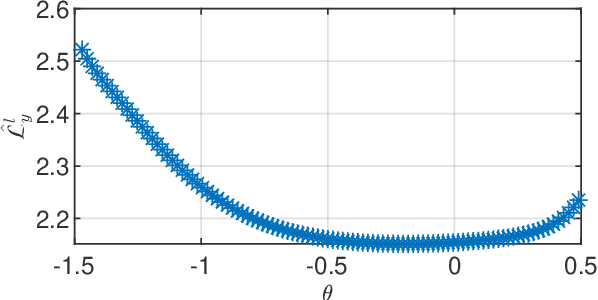
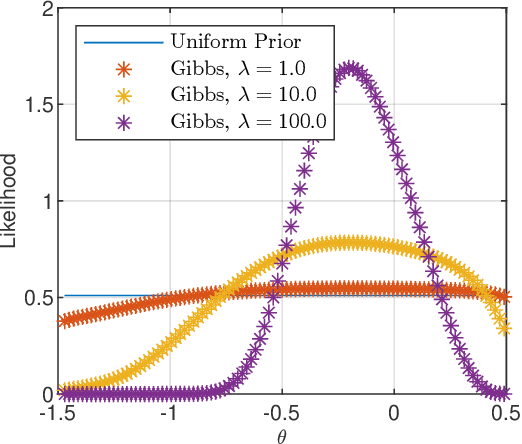
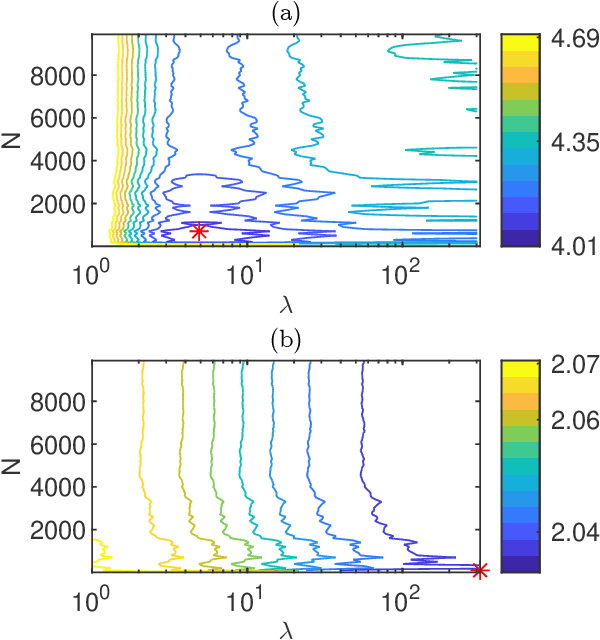
In this paper we derive a PAC-Bayesian error bound for autonomous stochastic LTI state-space models. The motivation for deriving such error bounds is that they will allow deriving similar error bounds for more general dynamical systems, including recurrent neural networks. In turn, PACBayesian error bounds are known to be useful for analyzing machine learning algorithms and for deriving new ones.

Improved PAC-Bayesian Bounds for Linear Regression

In this paper, we improve the PAC-Bayesian error bound for linear regression derived in Germain et al. [10]. The improvements are twofold. First, the proposed error bound is tighter, and converges to the generalization loss with a well-chosen temperature parameter. Second, the error bound also holds for training data that are not independently sampled. In particular, the error bound applies to certain time series generated by well-known classes of dynamical models, such as ARX models.