On the Convergence of Local Descent Methods in Federated Learning

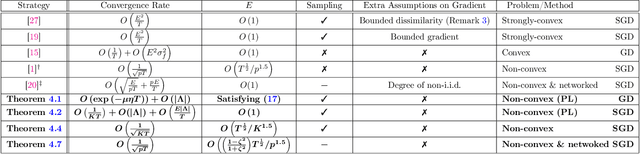
In federated distributed learning, the goal is to optimize a global training objective defined over distributed devices, where the data shard at each device is sampled from a possibly different distribution (a.k.a., heterogeneous or non i.i.d. data samples). In this paper, we generalize the local stochastic and full gradient descent with periodic averaging-- originally designed for homogeneous distributed optimization, to solve nonconvex optimization problems in federated learning. Although scant research is available on the effectiveness of local SGD in reducing the number of communication rounds in homogeneous setting, its convergence and communication complexity in heterogeneous setting is mostly demonstrated empirically and lacks through theoretical understating. To bridge this gap, we demonstrate that by properly analyzing the effect of unbiased gradients and sampling schema in federated setting, under mild assumptions, the implicit variance reduction feature of local distributed methods generalize to heterogeneous data shards and exhibits the best known convergence rates of homogeneous setting both in general nonconvex and under {\pl}~ condition (generalization of strong-convexity). Our theoretical results complement the recent empirical studies that demonstrate the applicability of local GD/SGD to federated learning. We also specialize the proposed local method for networked distributed optimization. To the best of our knowledge, the obtained convergence rates are the sharpest known to date on the convergence of local decant methods with periodic averaging for solving nonconvex federated optimization in both centralized and networked distributed optimization.

Efficient Fair Principal Component Analysis

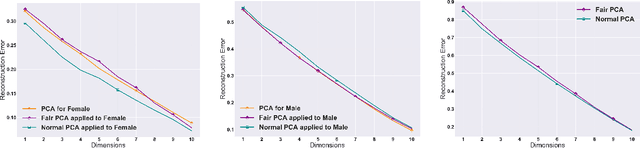
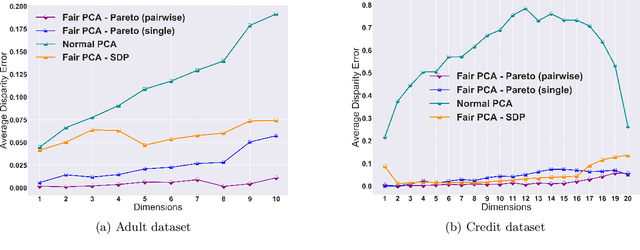
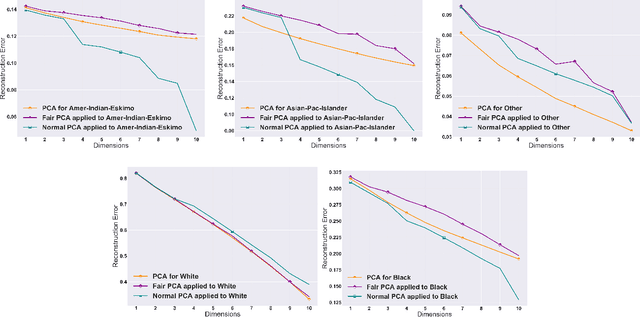
The flourishing assessments of fairness measure in machine learning algorithms have shown that dimension reduction methods such as PCA treat data from different sensitive groups unfairly. In particular, by aggregating data of different groups, the reconstruction error of the learned subspace becomes biased towards some populations that might hurt or benefit those groups inherently, leading to an unfair representation. On the other hand, alleviating the bias to protect sensitive groups in learning the optimal projection, would lead to a higher reconstruction error overall. This introduces a trade-off between sensitive groups' sacrifices and benefits, and the overall reconstruction error. In this paper, in pursuit of achieving fairness criteria in PCA, we introduce a more efficient notion of Pareto fairness, cast the Pareto fair dimensionality reduction as a multi-objective optimization problem, and propose an adaptive gradient-based algorithm to solve it. Using the notion of Pareto optimality, we can guarantee that the solution of our proposed algorithm belongs to the Pareto frontier for all groups, which achieves the optimal trade-off between those aforementioned conflicting objectives. This framework can be efficiently generalized to multiple group sensitive features, as well. We provide convergence analysis of our algorithm for both convex and non-convex objectives and show its efficacy through empirical studies on different datasets, in comparison with the state-of-the-art algorithm.

Local SGD with Periodic Averaging: Tighter Analysis and Adaptive Synchronization

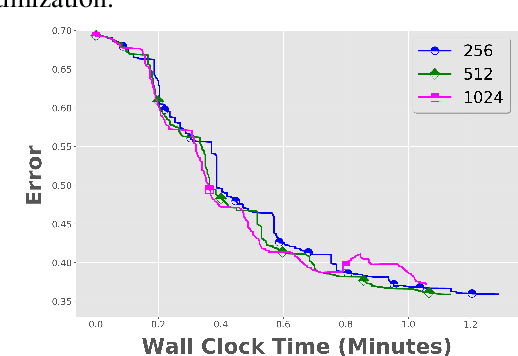
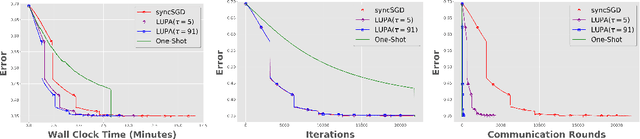
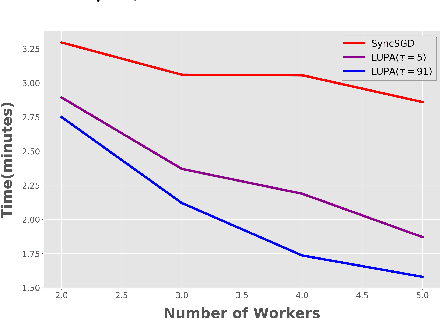
Communication overhead is one of the key challenges that hinders the scalability of distributed optimization algorithms. In this paper, we study local distributed SGD, where data is partitioned among computation nodes, and the computation nodes perform local updates with periodically exchanging the model among the workers to perform averaging. While local SGD is empirically shown to provide promising results, a theoretical understanding of its performance remains open. We strengthen convergence analysis for local SGD, and show that local SGD can be far less expensive and applied far more generally than current theory suggests. Specifically, we show that for loss functions that satisfy the Polyak-{\L}ojasiewicz condition, $O((pT)^{1/3})$ rounds of communication suffice to achieve a linear speed up, that is, an error of $O(1/pT)$, where $T$ is the total number of model updates at each worker. This is in contrast with previous work which required higher number of communication rounds, as well as was limited to strongly convex loss functions, for a similar asymptotic performance. We also develop an adaptive synchronization scheme that provides a general condition for linear speed up. Finally, we validate the theory with experimental results, running over AWS EC2 clouds and an internal GPU cluster.

Learning Feature Nonlinearities with Non-Convex Regularized Binned Regression

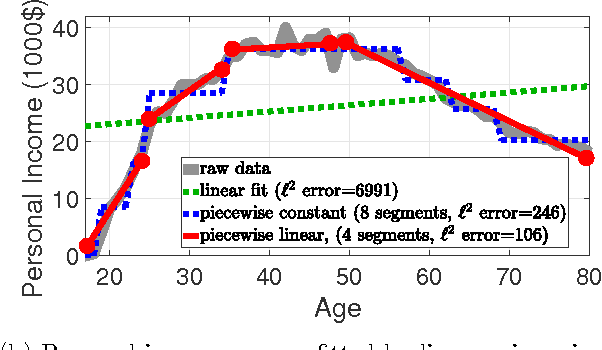
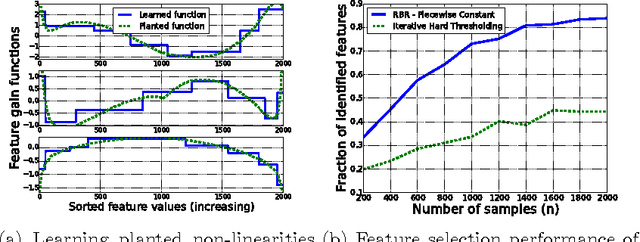
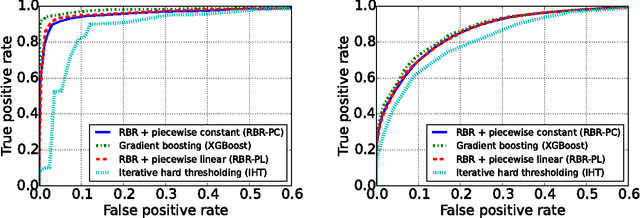
For various applications, the relations between the dependent and independent variables are highly nonlinear. Consequently, for large scale complex problems, neural networks and regression trees are commonly preferred over linear models such as Lasso. This work proposes learning the feature nonlinearities by binning feature values and finding the best fit in each quantile using non-convex regularized linear regression. The algorithm first captures the dependence between neighboring quantiles by enforcing smoothness via piecewise-constant/linear approximation and then selects a sparse subset of good features. We prove that the proposed algorithm is statistically and computationally efficient. In particular, it achieves linear rate of convergence while requiring near-minimal number of samples. Evaluations on synthetic and real datasets demonstrate that algorithm is competitive with current state-of-the-art and accurately learns feature nonlinearities. Finally, we explore an interesting connection between the binning stage of our algorithm and sparse Johnson-Lindenstrauss matrices.

Sketching Meets Random Projection in the Dual: A Provable Recovery Algorithm for Big and High-dimensional Data

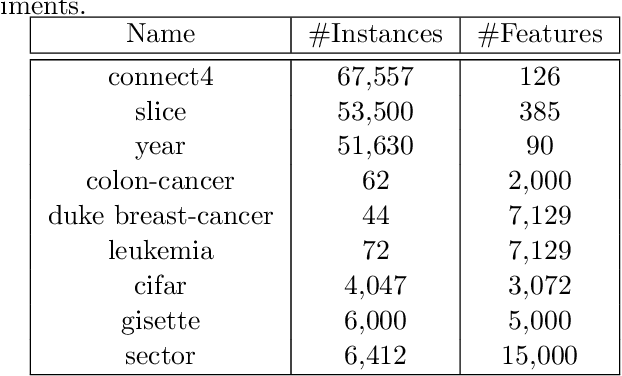
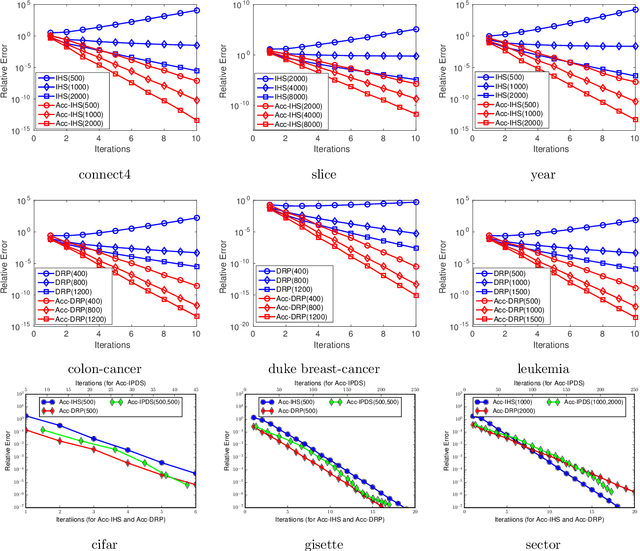
Sketching techniques have become popular for scaling up machine learning algorithms by reducing the sample size or dimensionality of massive data sets, while still maintaining the statistical power of big data. In this paper, we study sketching from an optimization point of view: we first show that the iterative Hessian sketch is an optimization process with preconditioning, and develop accelerated iterative Hessian sketch via the searching the conjugate direction; we then establish primal-dual connections between the Hessian sketch and dual random projection, and apply the preconditioned conjugate gradient approach on the dual problem, which leads to the accelerated iterative dual random projection methods. Finally to tackle the challenges from both large sample size and high-dimensionality, we propose the primal-dual sketch, which iteratively sketches the primal and dual formulations. We show that using a logarithmic number of calls to solvers of small scale problem, primal-dual sketch is able to recover the optimum of the original problem up to arbitrary precision. The proposed algorithms are validated via extensive experiments on synthetic and real data sets which complements our theoretical results.

Train and Test Tightness of LP Relaxations in Structured Prediction

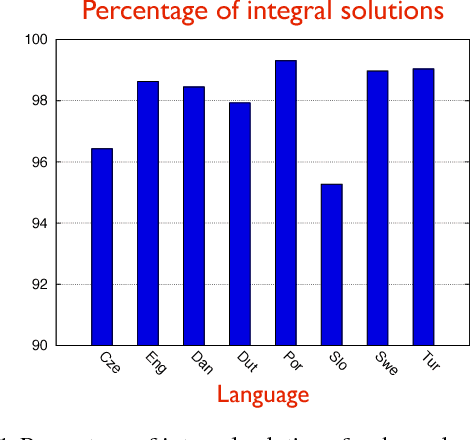
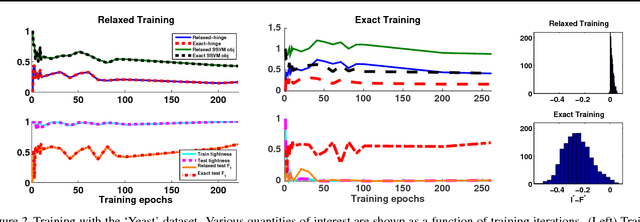
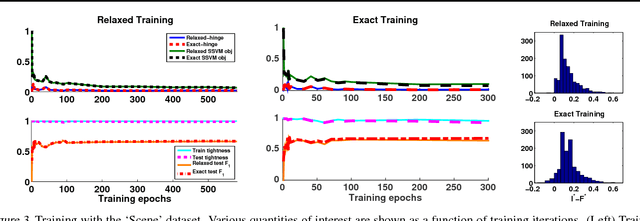
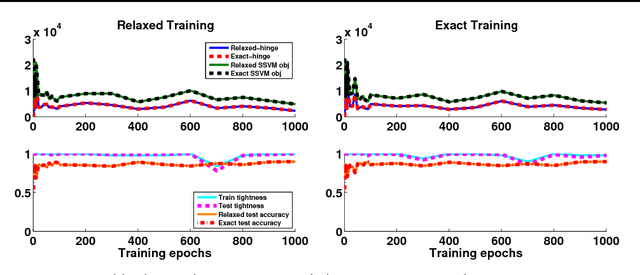
Structured prediction is used in areas such as computer vision and natural language processing to predict structured outputs such as segmentations or parse trees. In these settings, prediction is performed by MAP inference or, equivalently, by solving an integer linear program. Because of the complex scoring functions required to obtain accurate predictions, both learning and inference typically require the use of approximate solvers. We propose a theoretical explanation to the striking observation that approximations based on linear programming (LP) relaxations are often tight on real-world instances. In particular, we show that learning with LP relaxed inference encourages integrality of training instances, and that tightness generalizes from train to test data.

Matrix Factorization with Explicit Trust and Distrust Relationships

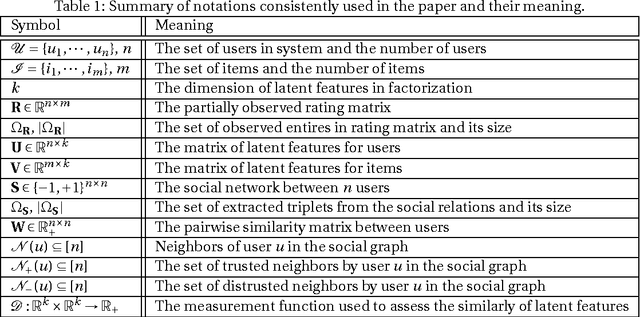
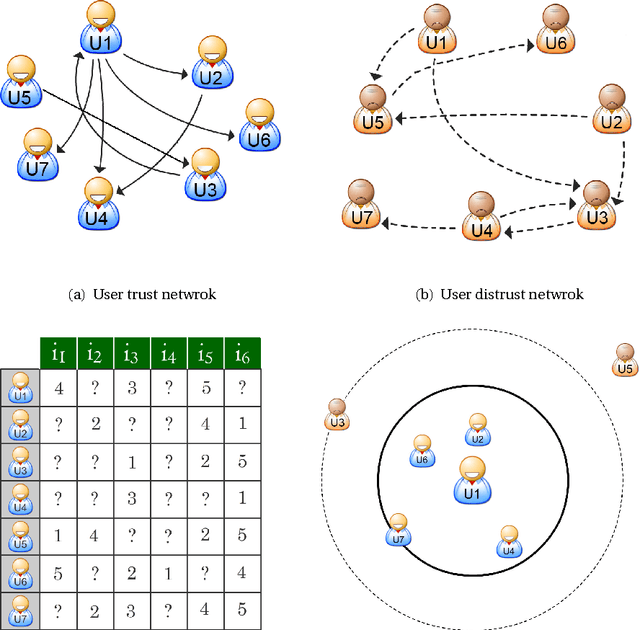
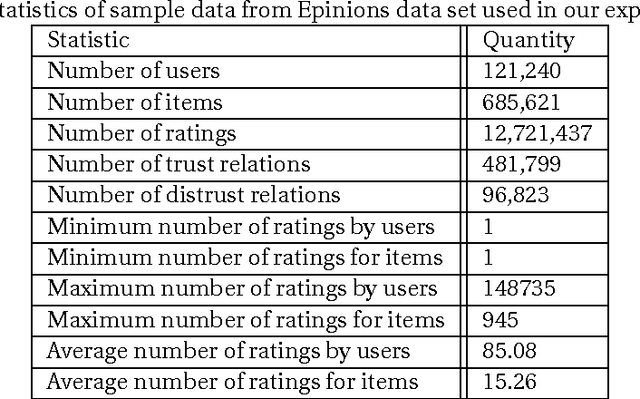
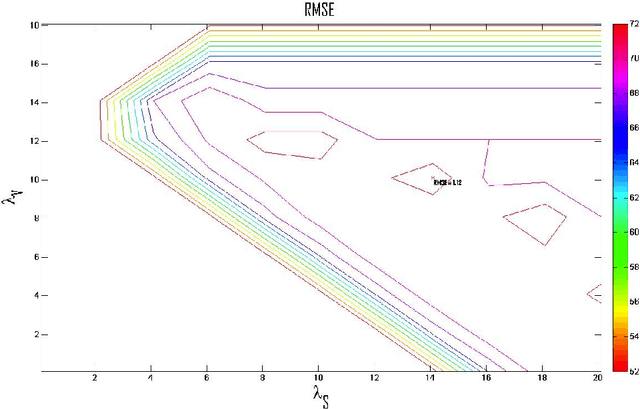
With the advent of online social networks, recommender systems have became crucial for the success of many online applications/services due to their significance role in tailoring these applications to user-specific needs or preferences. Despite their increasing popularity, in general recommender systems suffer from the data sparsity and the cold-start problems. To alleviate these issues, in recent years there has been an upsurge of interest in exploiting social information such as trust relations among users along with the rating data to improve the performance of recommender systems. The main motivation for exploiting trust information in recommendation process stems from the observation that the ideas we are exposed to and the choices we make are significantly influenced by our social context. However, in large user communities, in addition to trust relations, the distrust relations also exist between users. For instance, in Epinions the concepts of personal "web of trust" and personal "block list" allow users to categorize their friends based on the quality of reviews into trusted and distrusted friends, respectively. In this paper, we propose a matrix factorization based model for recommendation in social rating networks that properly incorporates both trust and distrust relationships aiming to improve the quality of recommendations and mitigate the data sparsity and the cold-start users issues. Through experiments on the Epinions data set, we show that our new algorithm outperforms its standard trust-enhanced or distrust-enhanced counterparts with respect to accuracy, thereby demonstrating the positive effect that incorporation of explicit distrust information can have on recommender systems.

Exploiting Smoothness in Statistical Learning, Sequential Prediction, and Stochastic Optimization

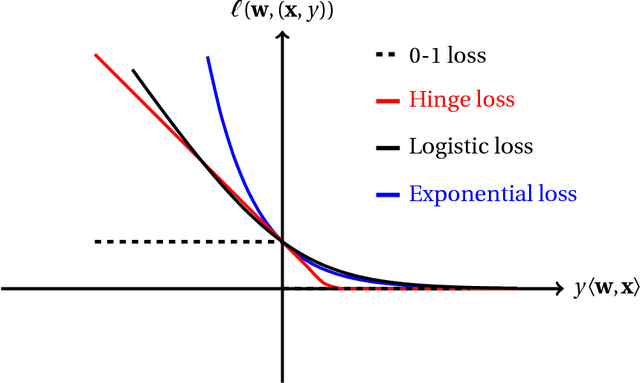
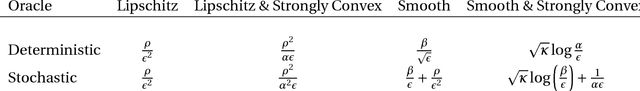
In the last several years, the intimate connection between convex optimization and learning problems, in both statistical and sequential frameworks, has shifted the focus of algorithmic machine learning to examine this interplay. In particular, on one hand, this intertwinement brings forward new challenges in reassessment of the performance of learning algorithms including generalization and regret bounds under the assumptions imposed by convexity such as analytical properties of loss functions (e.g., Lipschitzness, strong convexity, and smoothness). On the other hand, emergence of datasets of an unprecedented size, demands the development of novel and more efficient optimization algorithms to tackle large-scale learning problems. The overarching goal of this thesis is to reassess the smoothness of loss functions in statistical learning, sequential prediction/online learning, and stochastic optimization and explicate its consequences. In particular we examine how smoothness of loss function could be beneficial or detrimental in these settings in terms of sample complexity, statistical consistency, regret analysis, and convergence rate, and investigate how smoothness can be leveraged to devise more efficient learning algorithms.

Recovering the Optimal Solution by Dual Random Projection

Random projection has been widely used in data classification. It maps high-dimensional data into a low-dimensional subspace in order to reduce the computational cost in solving the related optimization problem. While previous studies are focused on analyzing the classification performance of using random projection, in this work, we consider the recovery problem, i.e., how to accurately recover the optimal solution to the original optimization problem in the high-dimensional space based on the solution learned from the subspace spanned by random projections. We present a simple algorithm, termed Dual Random Projection, that uses the dual solution of the low-dimensional optimization problem to recover the optimal solution to the original problem. Our theoretical analysis shows that with a high probability, the proposed algorithm is able to accurately recover the optimal solution to the original problem, provided that the data matrix is of low rank or can be well approximated by a low rank matrix.

Excess Risk Bounds for Exponentially Concave Losses

The overarching goal of this paper is to derive excess risk bounds for learning from exp-concave loss functions in passive and sequential learning settings. Exp-concave loss functions encompass several fundamental problems in machine learning such as squared loss in linear regression, logistic loss in classification, and negative logarithm loss in portfolio management. In batch setting, we obtain sharp bounds on the performance of empirical risk minimization performed in a linear hypothesis space and with respect to the exp-concave loss functions. We also extend the results to the online setting where the learner receives the training examples in a sequential manner. We propose an online learning algorithm that is a properly modified version of online Newton method to obtain sharp risk bounds. Under an additional mild assumption on the loss function, we show that in both settings we are able to achieve an excess risk bound of $O(d\log n/n)$ that holds with a high probability.