Mehdi Maadooliat
Regularized Multivariate Functional Principal Component Analysis
Jun 24, 2023



Abstract:Multivariate Functional Principal Component Analysis (MFPCA) is a valuable tool for exploring relationships and identifying shared patterns of variation in multivariate functional data. However, controlling the roughness of the extracted Principal Components (PCs) can be challenging. This paper introduces a novel approach called regularized MFPCA (ReMFPCA) to address this issue and enhance the smoothness and interpretability of the multivariate functional PCs. ReMFPCA incorporates a roughness penalty within a penalized framework, using a parameter vector to regulate the smoothness of each functional variable. The proposed method generates smoothed multivariate functional PCs, providing a concise and interpretable representation of the data. Extensive simulations and real data examples demonstrate the effectiveness of ReMFPCA and its superiority over alternative methods. The proposed approach opens new avenues for analyzing and uncovering relationships in complex multivariate functional datasets.
Functional Time Series Forecasting: Functional Singular Spectrum Analysis Approaches
Dec 18, 2020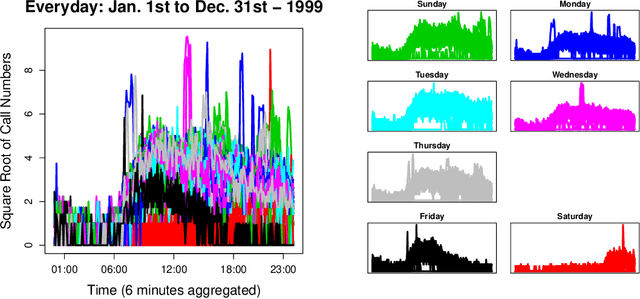
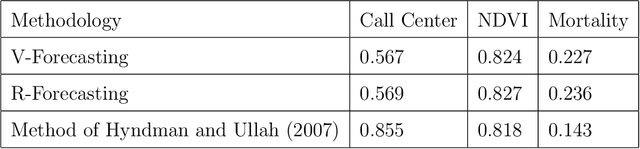
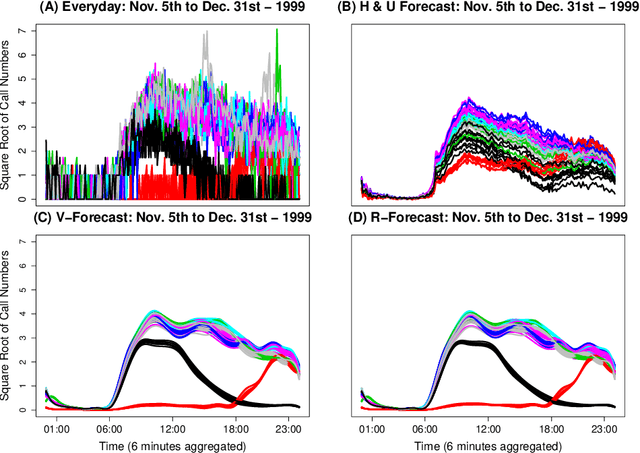
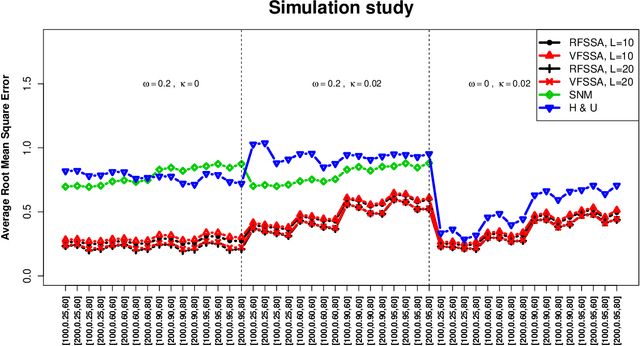
Abstract:In this paper, we propose two nonparametric methods used in the forecasting of functional time-dependent data, namely functional singular spectrum analysis recurrent forecasting and vector forecasting. Both algorithms utilize the results of functional singular spectrum analysis and past observations in order to predict future data points where recurrent forecasting predicts one function at a time and the vector forecasting makes predictions using functional vectors. We compare our forecasting methods to a gold standard algorithm used in the prediction of functional, time-dependent data by way of simulation and real data and we find our techniques do better for periodic stochastic processes.
Multivariate Functional Singular Spectrum Analysis Over Different Dimensional Domains
Jun 06, 2020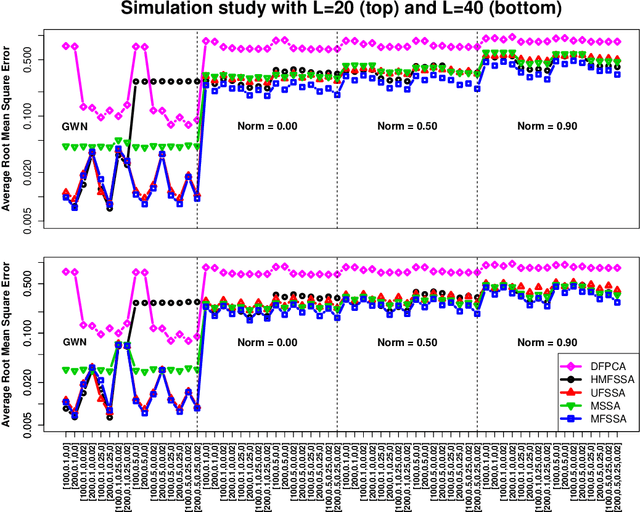
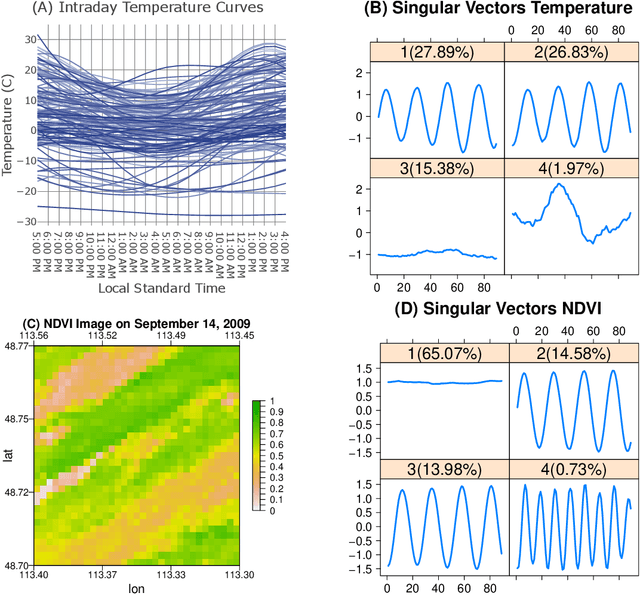
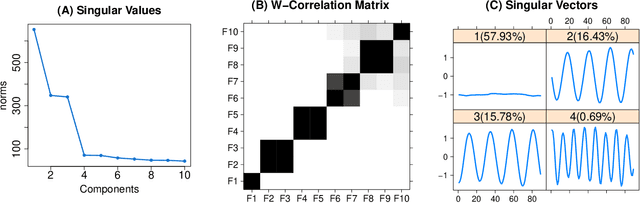
Abstract:In this work, we develop multivariate functional singular spectrum analysis (MFSSA) over different dimensional domains which is the functional extension of multivariate singular spectrum analysis (MSSA). In the following, we provide all of the necessary theoretical details supporting the work as well as the implementation strategy that contains the recipes needed for the algorithm. We provide a simulation study showcasing the better performance in reconstruction accuracy of a multivariate functional time series (MFTS) signal found using MFSSA as compared to other approaches and we give a real data study showing how MFSSA enriches analysis using intraday temperature curves and remote sensing images of vegetation. MFSSA is available for use through the Rfssa R package.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge