FP4 All the Way: Fully Quantized Training of LLMs

We demonstrate, for the first time, fully quantized training (FQT) of large language models (LLMs) using predominantly 4-bit floating-point (FP4) precision for weights, activations, and gradients on datasets up to 200 billion tokens. We extensively investigate key design choices for FP4, including block sizes, scaling formats, and rounding methods. Our analysis shows that the NVFP4 format, where each block of 16 FP4 values (E2M1) shares a scale represented in E4M3, provides optimal results. We use stochastic rounding for backward and update passes and round-to-nearest for the forward pass to enhance stability. Additionally, we identify a theoretical and empirical threshold for effective quantized training: when the gradient norm falls below approximately $\sqrt{3}$ times the quantization noise, quantized training becomes less effective. Leveraging these insights, we successfully train a 7-billion-parameter model on 256 Intel Gaudi2 accelerators. The resulting FP4-trained model achieves downstream task performance comparable to a standard BF16 baseline, confirming that FP4 training is a practical and highly efficient approach for large-scale LLM training. A reference implementation is supplied in https://github.com/Anonymous1252022/fp4-all-the-way .

EXAQ: Exponent Aware Quantization For LLMs Acceleration

Quantization has established itself as the primary approach for decreasing the computational and storage expenses associated with Large Language Models (LLMs) inference. The majority of current research emphasizes quantizing weights and activations to enable low-bit general-matrix-multiply (GEMM) operations, with the remaining non-linear operations executed at higher precision. In our study, we discovered that following the application of these techniques, the primary bottleneck in LLMs inference lies in the softmax layer. The softmax operation comprises three phases: exponent calculation, accumulation, and normalization, Our work focuses on optimizing the first two phases. We propose an analytical approach to determine the optimal clipping value for the input to the softmax function, enabling sub-4-bit quantization for LLMs inference. This method accelerates the calculations of both $e^x$ and $\sum(e^x)$ with minimal to no accuracy degradation. For example, in LLaMA1-30B, we achieve baseline performance with 2-bit quantization on the well-known "Physical Interaction: Question Answering" (PIQA) dataset evaluation. This ultra-low bit quantization allows, for the first time, an acceleration of approximately 4x in the accumulation phase. The combination of accelerating both $e^x$ and $\sum(e^x)$ results in a 36.9% acceleration in the softmax operation.

On Recoverability of Graph Neural Network Representations

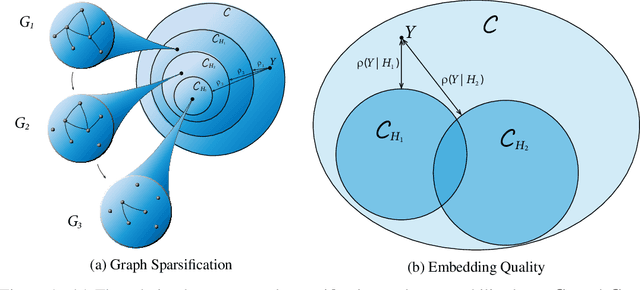
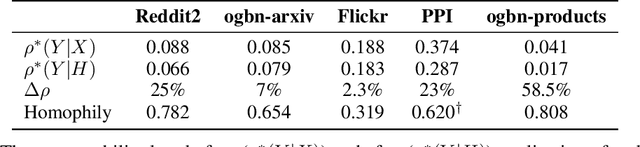
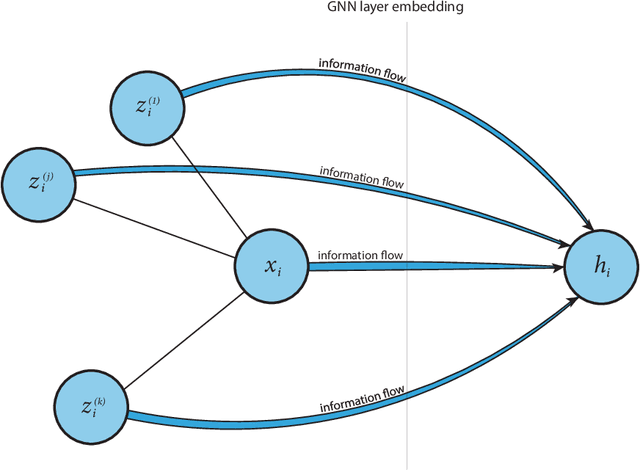
Despite their growing popularity, graph neural networks (GNNs) still have multiple unsolved problems, including finding more expressive aggregation methods, propagation of information to distant nodes, and training on large-scale graphs. Understanding and solving such problems require developing analytic tools and techniques. In this work, we propose the notion of recoverability, which is tightly related to information aggregation in GNNs, and based on this concept, develop the method for GNN embedding analysis. We define recoverability theoretically and propose a method for its efficient empirical estimation. We demonstrate, through extensive experimental results on various datasets and different GNN architectures, that estimated recoverability correlates with aggregation method expressivity and graph sparsification quality. Therefore, we believe that the proposed method could provide an essential tool for understanding the roots of the aforementioned problems, and potentially lead to a GNN design that overcomes them. The code to reproduce our experiments is available at https://github.com/Anonymous1252022/Recoverability