Actor-critic is implicitly biased towards high entropy optimal policies

We show that the simplest actor-critic method -- a linear softmax policy updated with TD through interaction with a linear MDP, but featuring no explicit regularization or exploration -- does not merely find an optimal policy, but moreover prefers high entropy optimal policies. To demonstrate the strength of this bias, the algorithm not only has no regularization, no projections, and no exploration like $\epsilon$-greedy, but is moreover trained on a single trajectory with no resets. The key consequence of the high entropy bias is that uniform mixing assumptions on the MDP, which exist in some form in all prior work, can be dropped: the implicit regularization of the high entropy bias is enough to ensure that all chains mix and an optimal policy is reached with high probability. As auxiliary contributions, this work decouples concerns between the actor and critic by writing the actor update as an explicit mirror descent, provides tools to uniformly bound mixing times within KL balls of policy space, and provides a projection-free TD analysis with its own implicit bias which can be run from an unmixed starting distribution.

Fast Margin Maximization via Dual Acceleration

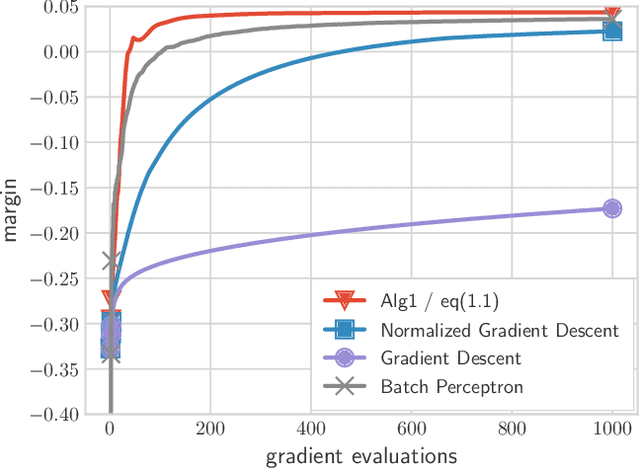
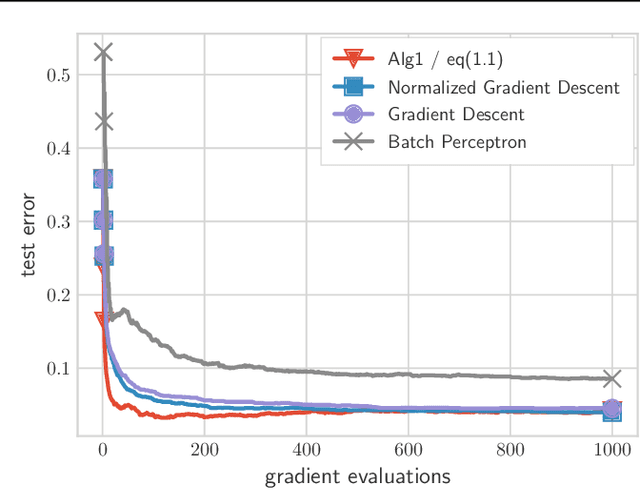
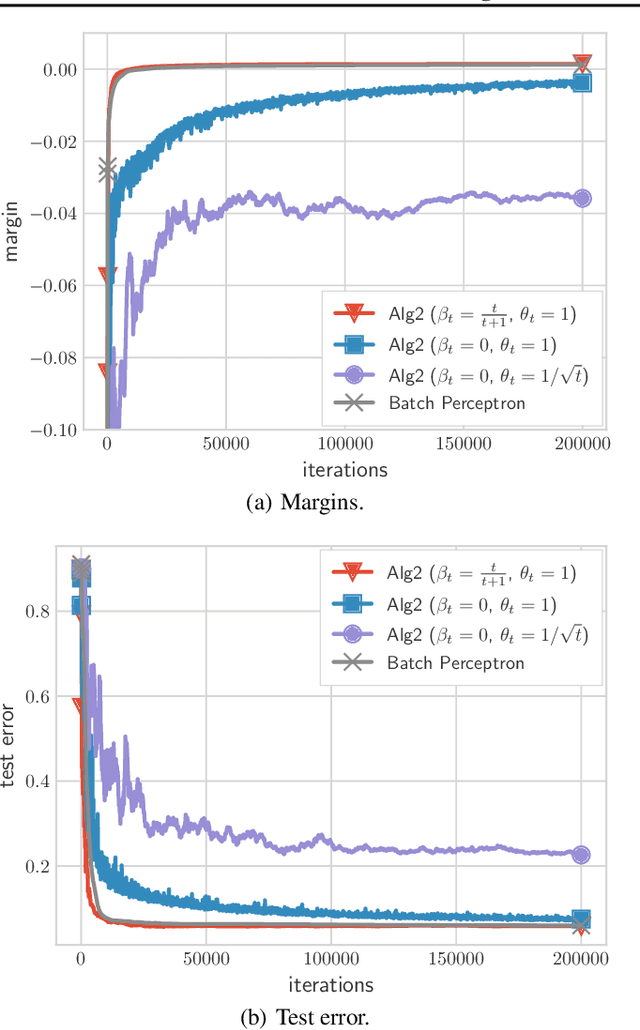
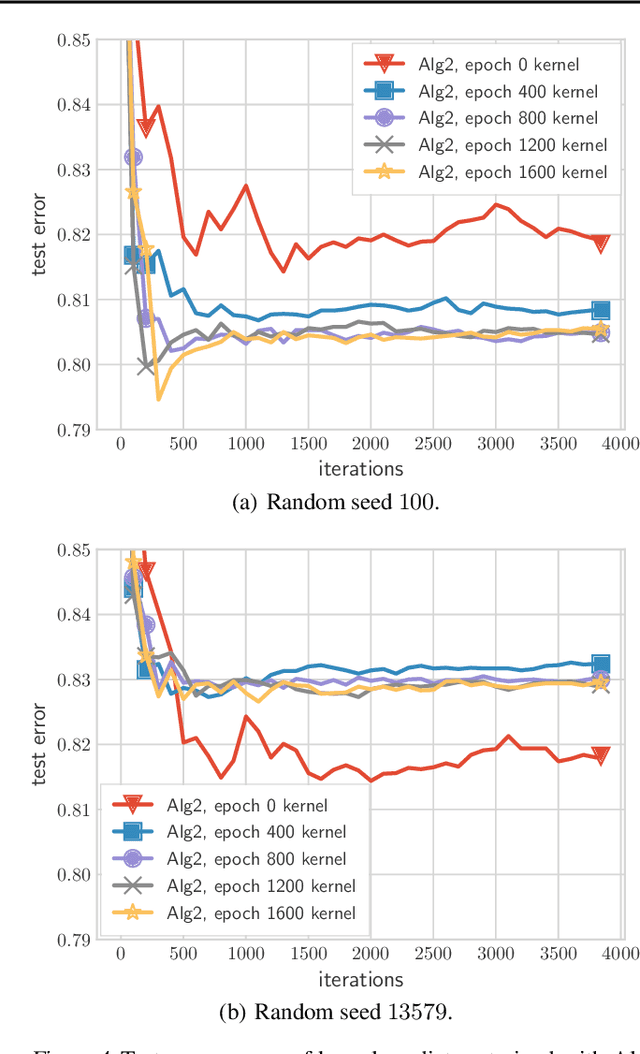
We present and analyze a momentum-based gradient method for training linear classifiers with an exponentially-tailed loss (e.g., the exponential or logistic loss), which maximizes the classification margin on separable data at a rate of $\widetilde{\mathcal{O}}(1/t^2)$. This contrasts with a rate of $\mathcal{O}(1/\log(t))$ for standard gradient descent, and $\mathcal{O}(1/t)$ for normalized gradient descent. This momentum-based method is derived via the convex dual of the maximum-margin problem, and specifically by applying Nesterov acceleration to this dual, which manages to result in a simple and intuitive method in the primal. This dual view can also be used to derive a stochastic variant, which performs adaptive non-uniform sampling via the dual variables.

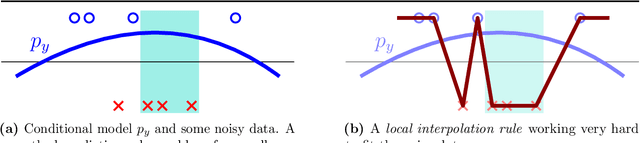
Early-stopped neural networks are consistent

This work studies the behavior of neural networks trained with the logistic loss via gradient descent on binary classification data where the underlying data distribution is general, and the (optimal) Bayes risk is not necessarily zero. In this setting, it is shown that gradient descent with early stopping achieves population risk arbitrarily close to optimal in terms of not just logistic and misclassification losses, but also in terms of calibration, meaning the sigmoid mapping of its outputs approximates the true underlying conditional distribution arbitrarily finely. Moreover, the necessary iteration, sample, and architectural complexities of this analysis all scale naturally with a certain complexity measure of the true conditional model. Lastly, while it is not shown that early stopping is necessary, it is shown that any univariate classifier satisfying a local interpolation property is necessarily inconsistent.

Generalization bounds via distillation

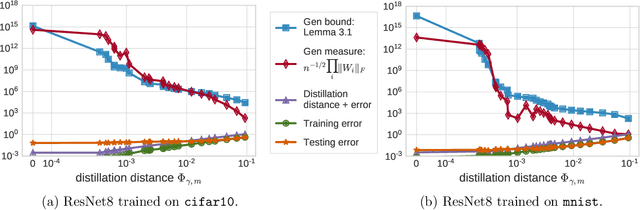
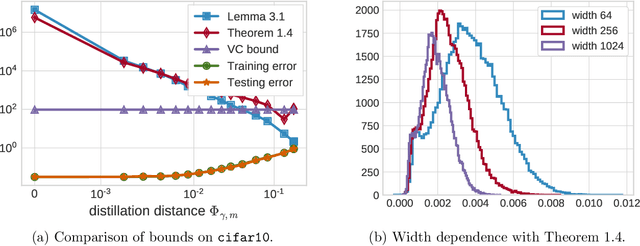
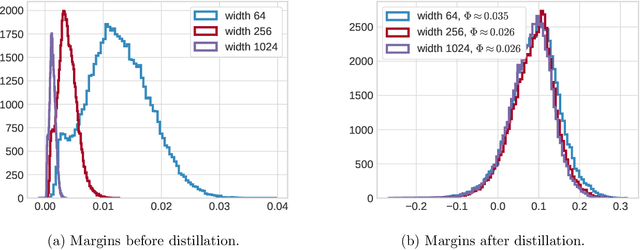
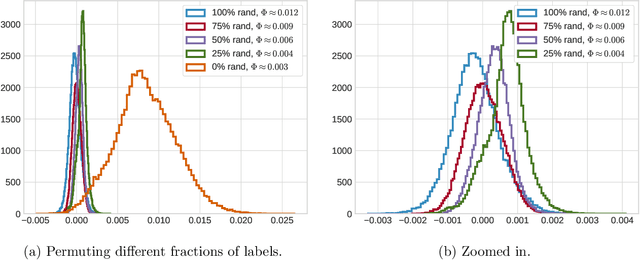
This paper theoretically investigates the following empirical phenomenon: given a high-complexity network with poor generalization bounds, one can distill it into a network with nearly identical predictions but low complexity and vastly smaller generalization bounds. The main contribution is an analysis showing that the original network inherits this good generalization bound from its distillation, assuming the use of well-behaved data augmentation. This bound is presented both in an abstract and in a concrete form, the latter complemented by a reduction technique to handle modern computation graphs featuring convolutional layers, fully-connected layers, and skip connections, to name a few. To round out the story, a (looser) classical uniform convergence analysis of compression is also presented, as well as a variety of experiments on cifar and mnist demonstrating similar generalization performance between the original network and its distillation.

Gradient descent follows the regularization path for general losses

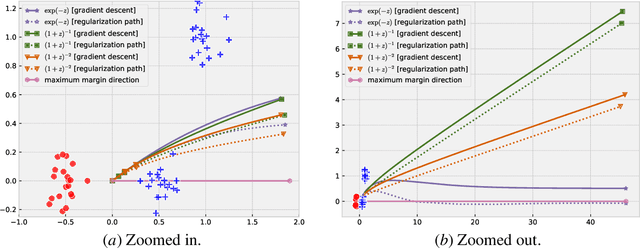
Recent work across many machine learning disciplines has highlighted that standard descent methods, even without explicit regularization, do not merely minimize the training error, but also exhibit an implicit bias. This bias is typically towards a certain regularized solution, and relies upon the details of the learning process, for instance the use of the cross-entropy loss. In this work, we show that for empirical risk minimization over linear predictors with arbitrary convex, strictly decreasing losses, if the risk does not attain its infimum, then the gradient-descent path and the algorithm-independent regularization path converge to the same direction (whenever either converges to a direction). Using this result, we provide a justification for the widely-used exponentially-tailed losses (such as the exponential loss or the logistic loss): while this convergence to a direction for exponentially-tailed losses is necessarily to the maximum-margin direction, other losses such as polynomially-tailed losses may induce convergence to a direction with a poor margin.

Directional convergence and alignment in deep learning

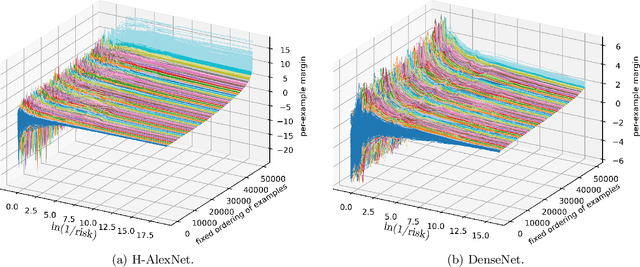
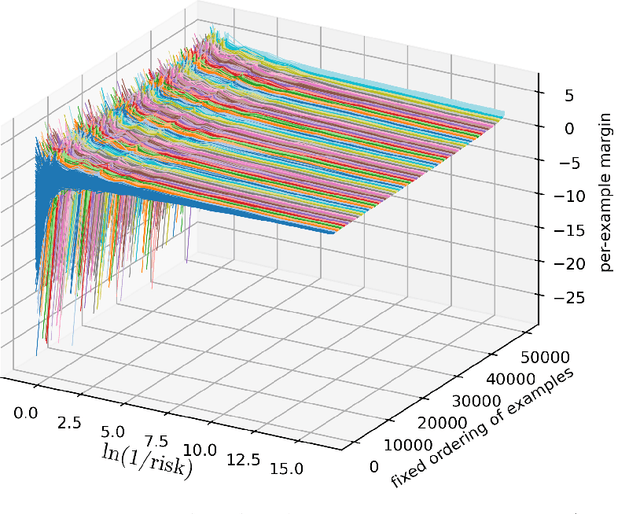
In this paper, we show that although the minimizers of cross-entropy and related classification losses are off at infinity, network weights learned by gradient flow converge in direction, with an immediate corollary that network predictions, training errors, and the margin distribution also converge. This proof holds for deep homogeneous networks -- a broad class of networks allowing for ReLU, max pooling, linear, and convolutional layers -- and we additionally provide empirical support not just close to the theory (e.g., the AlexNet), but also on non-homogeneous networks (e.g., the ResNet). If the network further has locally Lipschitz gradients, we show that these gradients converge in direction, and asymptotically align with the gradient flow path, with consequences on margin maximization. Our analysis complements and is distinct from the well-known neural tangent and mean-field theories, and in particular makes no requirements on network width and initialization, instead merely requiring perfect classification accuracy. The proof proceeds by developing a theory of unbounded nonsmooth Kurdyka-Lojasiewicz inequalities for functions definable in an o-minimal structure, and is also applicable outside deep learning.

Neural tangent kernels, transportation mappings, and universal approximation

This paper establishes rates of universal approximation for the shallow neural tangent kernel (NTK): network weights are only allowed microscopic changes from random initialization, which entails that activations are mostly unchanged, and the network is nearly equivalent to its linearization. Concretely, the paper has two main contributions: a generic scheme to approximate functions with the NTK by sampling from transport mappings between the initial weights and their desired values, and the construction of transport mappings via Fourier transforms. Regarding the first contribution, the proof scheme provides another perspective on how the NTK regime arises from rescaling: redundancy in the weights due to resampling allows individual weights to be scaled down. Regarding the second contribution, the most notable transport mapping asserts that roughly $1 / \delta^{10d}$ nodes are sufficient to approximate continuous functions, where $\delta$ depends on the continuity properties of the target function. By contrast, nearly the same proof yields a bound of $1 / \delta^{2d}$ for shallow ReLU networks; this gap suggests a tantalizing direction for future work, separating shallow ReLU networks and their linearization.

Polylogarithmic width suffices for gradient descent to achieve arbitrarily small test error with shallow ReLU networks

Recent theoretical work has guaranteed that overparameterized networks trained by gradient descent achieve arbitrarily low training error, and sometimes even low test error. The required width, however, is always polynomial in at least one of the sample size $n$, the (inverse) target error $1/\epsilon$, and the (inverse) failure probability $1/\delta$. This work shows that $\widetilde{O}(1/\epsilon)$ iterations of gradient descent with $\widetilde{\Omega}(1/\epsilon^2)$ training examples on two-layer ReLU networks of any width exceeding $\mathrm{polylog}(n,1/\epsilon,1/\delta)$ suffice to achieve a test misclassification error of $\epsilon$. The analysis further relies upon a margin property of the limiting kernel, which is guaranteed positive, and can distinguish between true labels and random labels.

Approximation power of random neural networks

This paper investigates the approximation power of three types of random neural networks: (a) infinite width networks, with weights following an arbitrary distribution; (b) finite width networks obtained by subsampling the preceding infinite width networks; (c) finite width networks obtained by starting with standard Gaussian initialization, and then adding a vanishingly small correction to the weights. The primary result is a fully quantified bound on the rate of approximation of general general continuous functions: in all three cases, a function $f$ can be approximated with complexity $\|f\|_1 (d/\delta)^{\mathcal{O}(d)}$, where $\delta$ depends on continuity properties of $f$ and the complexity measure depends on the weight magnitudes and/or cardinalities. Along the way, a variety of ancillary results are developed: an exact construction of Gaussian densities with infinite width networks, an elementary stand-alone proof scheme for approximation via convolutions of radial basis functions, subsampling rates for infinite width networks, and depth separation for corrected networks.

A gradual, semi-discrete approach to generative network training via explicit Wasserstein minimization

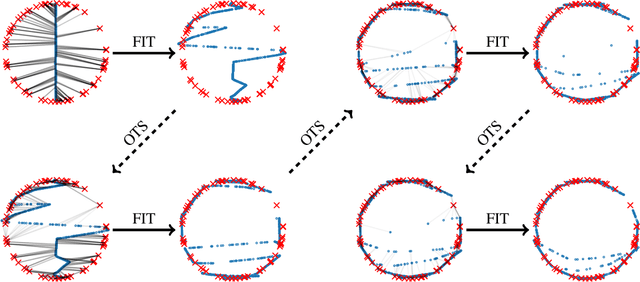
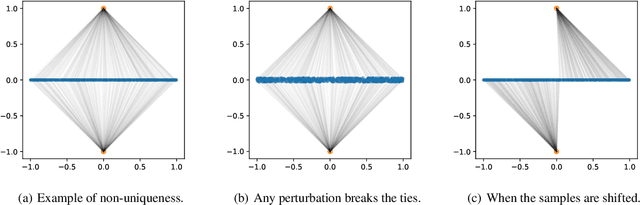
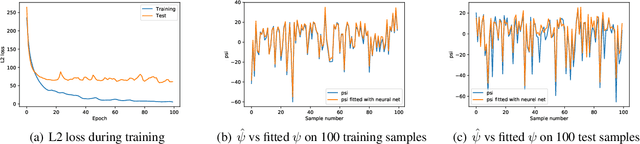
This paper provides a simple procedure to fit generative networks to target distributions, with the goal of a small Wasserstein distance (or other optimal transport costs). The approach is based on two principles: (a) if the source randomness of the network is a continuous distribution (the "semi-discrete" setting), then the Wasserstein distance is realized by a deterministic optimal transport mapping; (b) given an optimal transport mapping between a generator network and a target distribution, the Wasserstein distance may be decreased via a regression between the generated data and the mapped target points. The procedure here therefore alternates these two steps, forming an optimal transport and regressing against it, gradually adjusting the generator network towards the target distribution. Mathematically, this approach is shown to minimize the Wasserstein distance to both the empirical target distribution, and also its underlying population counterpart. Empirically, good performance is demonstrated on the training and testing sets of the MNIST and Thin-8 data. The paper closes with a discussion of the unsuitability of the Wasserstein distance for certain tasks, as has been identified in prior work [Arora et al., 2017, Huang et al., 2017].