Benchmarking Quantum Kernels Across Diverse and Complex Data

Quantum kernel methods are a promising branch of quantum machine learning, yet their practical advantage on diverse, high-dimensional, real-world data remains unverified. Current research has largely been limited to low-dimensional or synthetic datasets, preventing a thorough evaluation of their potential. To address this gap, we developed a variational quantum kernel framework utilizing resource-efficient ansätze for complex classification tasks and introduced a parameter scaling technique to accelerate convergence. We conducted a comprehensive benchmark of this framework on eight challenging, real world and high-dimensional datasets covering tabular, image, time series, and graph data. Our classically simulated results show that the proposed quantum kernel demonstrated a clear performance advantage over standard classical kernels, such as the radial basis function (RBF) kernel. This work demonstrates that properly designed quantum kernels can function as versatile, high-performance tools, laying a foundation for quantum-enhanced applications in real-world machine learning. Further research is needed to fully assess the practical quantum advantage.

Quantum Kerr Learning

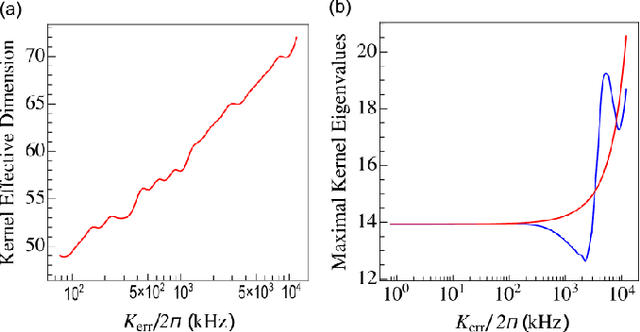
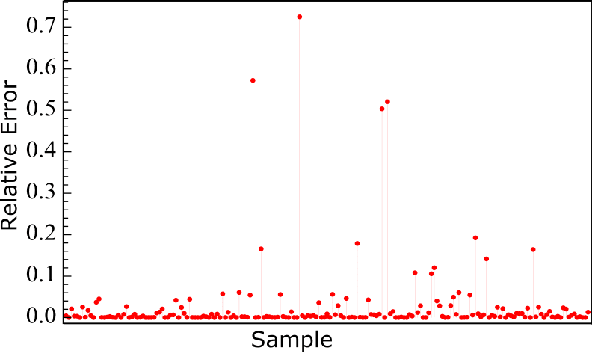
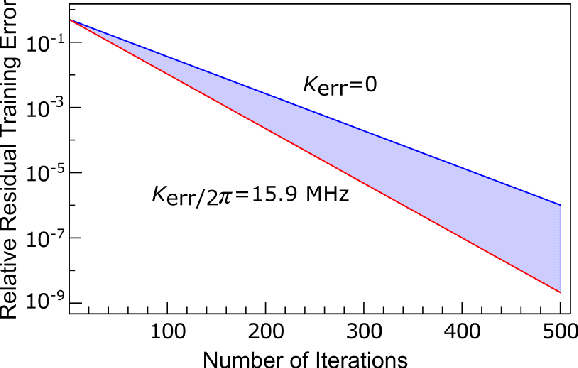
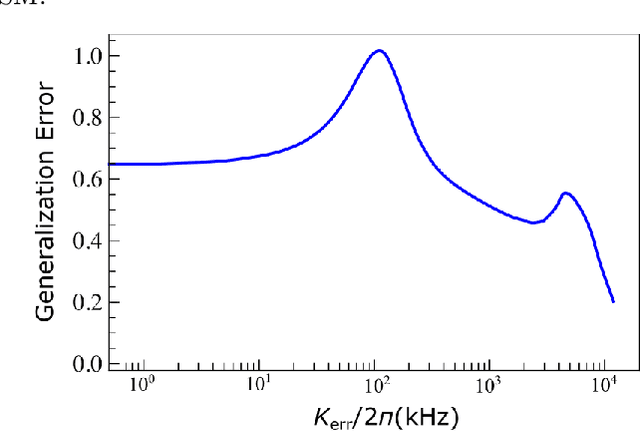
Quantum machine learning is a rapidly evolving area that could facilitate important applications for quantum computing and significantly impact data science. In our work, we argue that a single Kerr mode might provide some extra quantum enhancements when using quantum kernel methods based on various reasons from complexity theory and physics. Furthermore, we establish an experimental protocol, which we call \emph{quantum Kerr learning} based on circuit QED. A detailed study using the kernel method, neural tangent kernel theory, first-order perturbation theory of the Kerr non-linearity, and non-perturbative numerical simulations, shows quantum enhancements could happen in terms of the convergence time and the generalization error, while explicit protocols are also constructed for higher-dimensional input data.