How To Discover Short, Shorter, and the Shortest Proofs of Unsatisfiability: A Branch-and-Bound Approach for Resolution Proof Length Minimization

Modern software for propositional satisfiability problems gives a powerful automated reasoning toolkit, capable of outputting not only a satisfiable/unsatisfiable signal but also a justification of unsatisfiability in the form of resolution proof (or a more expressive proof), which is commonly used for verification purposes. Empirically, modern SAT solvers produce relatively short proofs, however, there are no inherent guarantees that these proofs cannot be significantly reduced. This paper proposes a novel branch-and-bound algorithm for finding the shortest resolution proofs; to this end, we introduce a layer list representation of proofs that groups clauses by their level of indirection. As we show, this representation breaks all permutational symmetries, thereby improving upon the state-of-the-art symmetry-breaking and informing the design of a novel workflow for proof minimization. In addition to that, we design pruning procedures that reason on proof length lower bound, clause subsumption, and dominance. Our experiments suggest that the proofs from state-of-the-art solvers could be shortened by 30-60% on the instances from SAT Competition 2002 and by 25-50% on small synthetic formulas. When treated as an algorithm for finding the shortest proof, our approach solves twice as many instances as the previous work based on SAT solving and reduces the time to optimality by orders of magnitude for the instances solved by both approaches.

Proactive and Reactive Constraint Programming for Stochastic Project Scheduling with Maximal Time-Lags

This study investigates scheduling strategies for the stochastic resource-constrained project scheduling problem with maximal time lags (SRCPSP/max)). Recent advances in Constraint Programming (CP) and Temporal Networks have reinvoked interest in evaluating the advantages and drawbacks of various proactive and reactive scheduling methods. First, we present a new, CP-based fully proactive method. Second, we show how a reactive approach can be constructed using an online rescheduling procedure. A third contribution is based on partial order schedules and uses Simple Temporal Networks with Uncertainty (STNUs). Our statistical analysis shows that the STNU-based algorithm performs best in terms of solution quality, while also showing good relative offline and online computation time.

A Penalty-Based Guardrail Algorithm for Non-Decreasing Optimization with Inequality Constraints

Traditional mathematical programming solvers require long computational times to solve constrained minimization problems of complex and large-scale physical systems. Therefore, these problems are often transformed into unconstrained ones, and solved with computationally efficient optimization approaches based on first-order information, such as the gradient descent method. However, for unconstrained problems, balancing the minimization of the objective function with the reduction of constraint violations is challenging. We consider the class of time-dependent minimization problems with increasing (possibly) nonlinear and non-convex objective function and non-decreasing (possibly) nonlinear and non-convex inequality constraints. To efficiently solve them, we propose a penalty-based guardrail algorithm (PGA). This algorithm adapts a standard penalty-based method by dynamically updating the right-hand side of the constraints with a guardrail variable which adds a margin to prevent violations. We evaluate PGA on two novel application domains: a simplified model of a district heating system and an optimization model derived from learned deep neural networks. Our method significantly outperforms mathematical programming solvers and the standard penalty-based method, and achieves better performance and faster convergence than a state-of-the-art algorithm (IPDD) within a specified time limit.

To the Max: Reinventing Reward in Reinforcement Learning

In reinforcement learning (RL), different rewards can define the same optimal policy but result in drastically different learning performance. For some, the agent gets stuck with a suboptimal behavior, and for others, it solves the task efficiently. Choosing a good reward function is hence an extremely important yet challenging problem. In this paper, we explore an alternative approach to using rewards for learning. We introduce max-reward RL, where an agent optimizes the maximum rather than the cumulative reward. Unlike earlier works, our approach works for deterministic and stochastic environments and can be easily combined with state-of-the-art RL algorithms. In the experiments, we study the performance of max-reward RL algorithms in two goal-reaching environments from Gymnasium-Robotics and demonstrate its benefits over standard RL. The code is publicly available.

Learning From Scenarios for Stochastic Repairable Scheduling

When optimizing problems with uncertain parameter values in a linear objective, decision-focused learning enables end-to-end learning of these values. We are interested in a stochastic scheduling problem, in which processing times are uncertain, which brings uncertain values in the constraints, and thus repair of an initial schedule may be needed. Historical realizations of the stochastic processing times are available. We show how existing decision-focused learning techniques based on stochastic smoothing can be adapted to this scheduling problem. We include an extensive experimental evaluation to investigate in which situations decision-focused learning outperforms the state of the art for such situations: scenario-based stochastic optimization.

You Shall not Pass: the Zero-Gradient Problem in Predict and Optimize for Convex Optimization

Predict and optimize is an increasingly popular decision-making paradigm that employs machine learning to predict unknown parameters of optimization problems. Instead of minimizing the prediction error of the parameters, it trains predictive models using task performance as a loss function. In the convex optimization domain, predict and optimize has seen significant progress due to recently developed methods for differentiating optimization problem solutions over the problem parameters. This paper identifies a yet unnoticed drawback of this approach -- the zero-gradient problem -- and introduces a method to solve it. The suggested method is based on the mathematical properties of differential optimization and is verified using two real-world benchmarks.

EXPObench: Benchmarking Surrogate-based Optimisation Algorithms on Expensive Black-box Functions

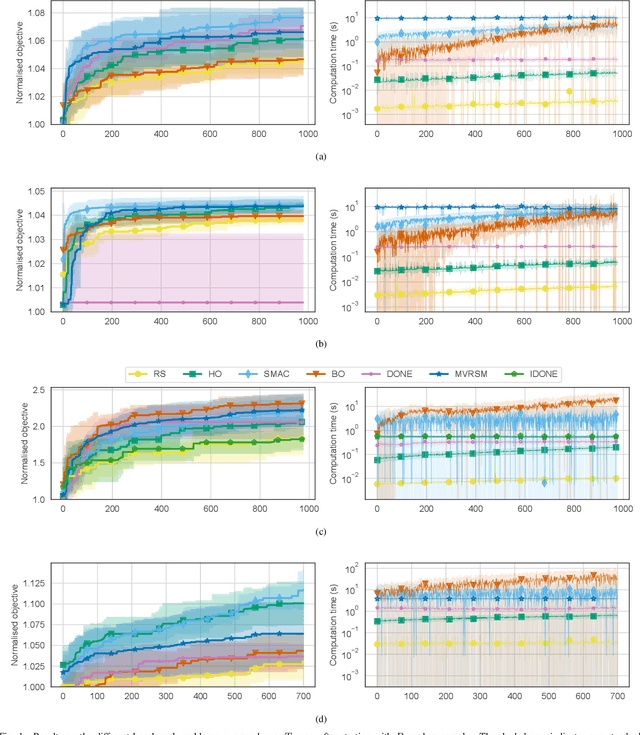
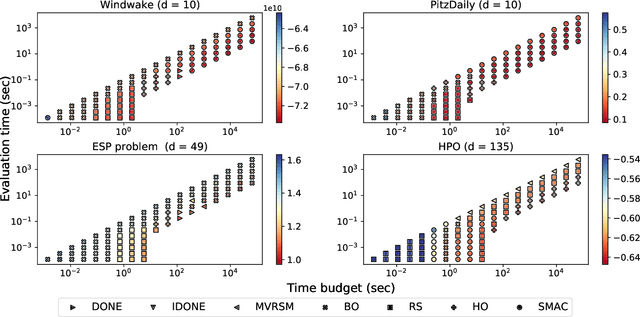
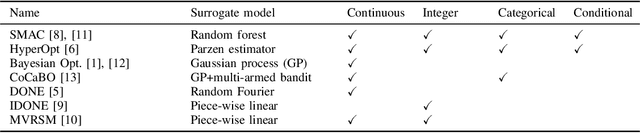
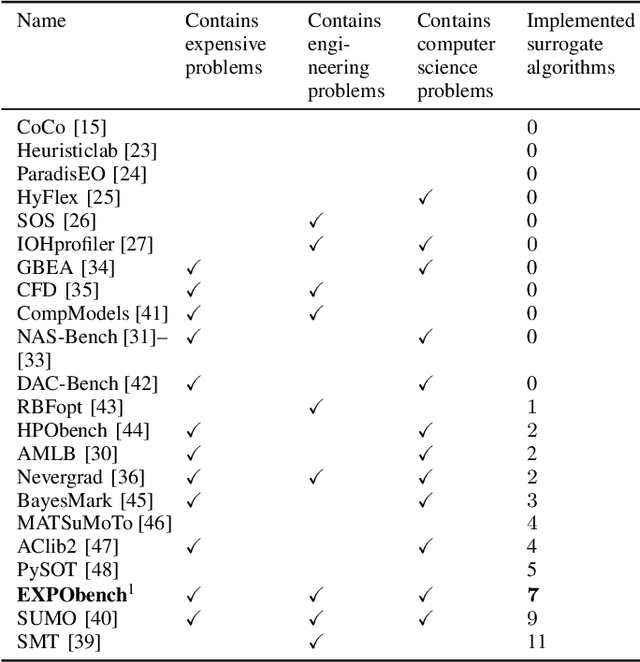
Surrogate algorithms such as Bayesian optimisation are especially designed for black-box optimisation problems with expensive objectives, such as hyperparameter tuning or simulation-based optimisation. In the literature, these algorithms are usually evaluated with synthetic benchmarks which are well established but have no expensive objective, and only on one or two real-life applications which vary wildly between papers. There is a clear lack of standardisation when it comes to benchmarking surrogate algorithms on real-life, expensive, black-box objective functions. This makes it very difficult to draw conclusions on the effect of algorithmic contributions. A new benchmark library, EXPObench, provides first steps towards such a standardisation. The library is used to provide an extensive comparison of six different surrogate algorithms on four expensive optimisation problems from different real-life applications. This has led to new insights regarding the relative importance of exploration, the evaluation time of the objective, and the used model. A further contribution is that we make the algorithms and benchmark problem instances publicly available, contributing to more uniform analysis of surrogate algorithms. Most importantly, we include the performance of the six algorithms on all evaluated problem instances. This results in a unique new dataset that lowers the bar for researching new methods as the number of expensive evaluations required for comparison is significantly reduced.

ReproducedPapers.org: Openly teaching and structuring machine learning reproducibility

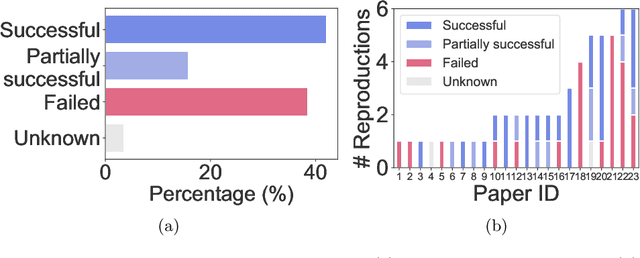
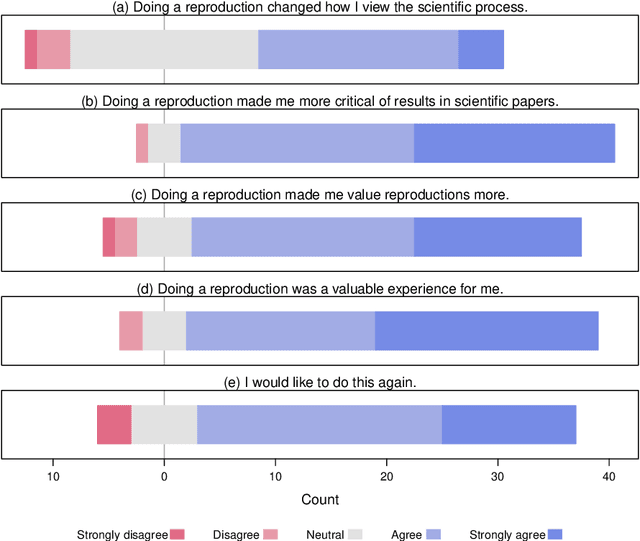
We present ReproducedPapers.org: an open online repository for teaching and structuring machine learning reproducibility. We evaluate doing a reproduction project among students and the added value of an online reproduction repository among AI researchers. We use anonymous self-assessment surveys and obtained 144 responses. Results suggest that students who do a reproduction project place more value on scientific reproductions and become more critical thinkers. Students and AI researchers agree that our online reproduction repository is valuable.

Continuous surrogate-based optimization algorithms are well-suited for expensive discrete problems

One method to solve expensive black-box optimization problems is to use a surrogate model that approximates the objective based on previous observed evaluations. The surrogate, which is cheaper to evaluate, is optimized instead to find an approximate solution to the original problem. In the case of discrete problems, recent research has revolved around surrogate models that are specifically constructed to deal with discrete structures. A main motivation is that literature considers continuous methods, such as Bayesian optimization with Gaussian processes as the surrogate, to be sub-optimal (especially in higher dimensions) because they ignore the discrete structure by e.g. rounding off real-valued solutions to integers. However, we claim that this is not true. In fact, we present empirical evidence showing that the use of continuous surrogate models displays competitive performance on a set of high-dimensional discrete benchmark problems, including a real-life application, against state-of-the-art discrete surrogate-based methods. Our experiments on different discrete structures and time constraints also give more insight into which algorithms work well on which type of problem.

Black-box Mixed-Variable Optimisation using a Surrogate Model that Satisfies Integer Constraints

A challenging problem in both engineering and computer science is that of minimising a function for which we have no mathematical formulation available, that is expensive to evaluate, and that contains continuous and integer variables, for example in automatic algorithm configuration. Surrogate modelling techniques are very suitable for this type of problem, but most existing techniques are designed with only continuous or only discrete variables in mind. Mixed-Variable ReLU-based Surrogate Modelling (MVRSM) is a surrogate modelling algorithm that uses a linear combination of rectified linear units, defined in such a way that (local) optima satisfy the integer constraints. This method is both more accurate and more efficient than the state of the art on several benchmarks with up to 238 continuous and integer variables.