A robust and adaptive MPC formulation for Gaussian process models

In this paper, we present a robust and adaptive model predictive control (MPC) framework for uncertain nonlinear systems affected by bounded disturbances and unmodeled nonlinearities. We use Gaussian Processes (GPs) to learn the uncertain dynamics based on noisy measurements, including those collected during system operation. As a key contribution, we derive robust predictions for GP models using contraction metrics, which are incorporated in the MPC formulation. The proposed design guarantees recursive feasibility, robust constraint satisfaction and convergence to a reference state, with high probability. We provide a numerical example of a planar quadrotor subject to difficult-to-model ground effects, which highlights significant improvements achieved through the proposed robust prediction method and through online learning.

Sim-to-Real for Soft Robots using Differentiable FEM: Recipes for Meshing, Damping, and Actuation

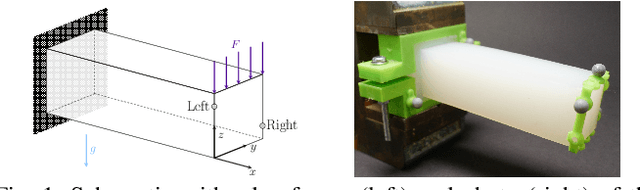
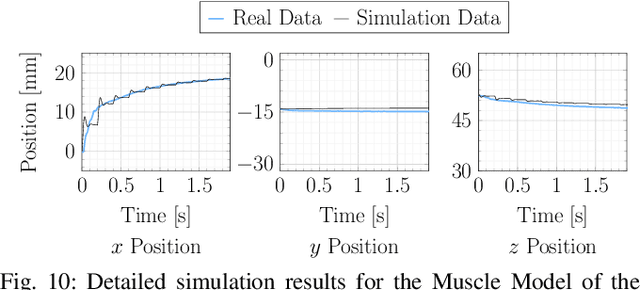
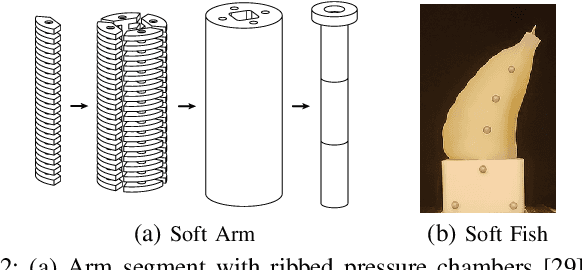
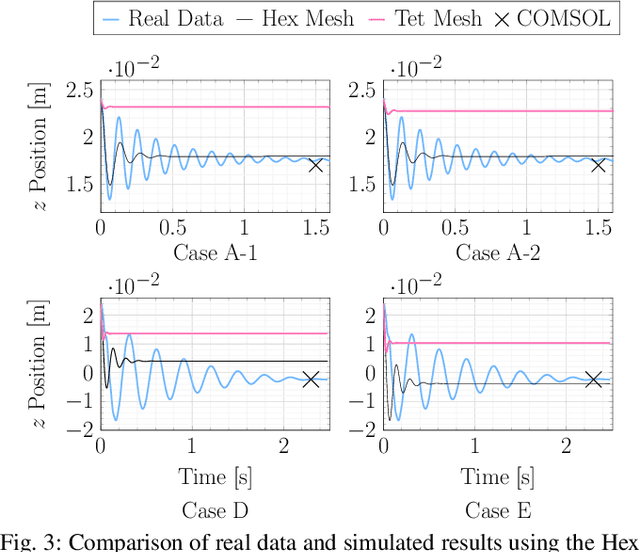
An accurate, physically-based, and differentiable model of soft robots can unlock downstream applications in optimal control. The Finite Element Method (FEM) is an expressive approach for modeling highly deformable structures such as dynamic, elastomeric soft robots. In this paper, we compare virtual robot models simulated using differentiable FEM with measurements from their physical counterparts. In particular, we examine several soft structures with different morphologies: a clamped soft beam under external force, a pneumatically actuated soft robotic arm, and a soft robotic fish tail. We benchmark and analyze different meshing resolutions and elements (tetrahedra and hexahedra), numerical damping, and the efficacy of differentiability for parameter calibration using a simulator based on the fast Differentiable Projective Dynamics (DiffPD). We also advance FEM modeling in application to soft robotics by proposing a predictive model for pneumatic soft robotic actuation. Through our recipes and case studies, we provide strategies and algorithms for matching real-world physics in simulation, making FEM useful for soft robots