3D Steerable CNNs: Learning Rotationally Equivariant Features in Volumetric Data

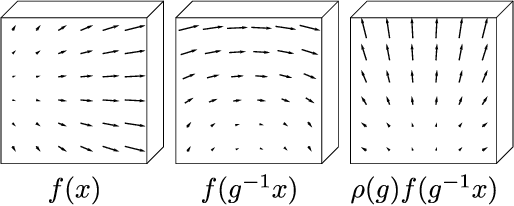
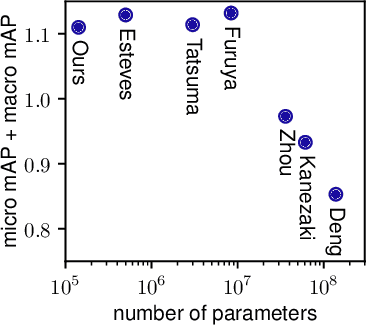
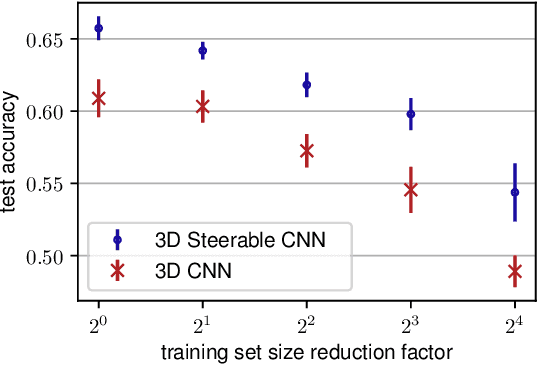
We present a convolutional network that is equivariant to rigid body motions. The model uses scalar-, vector-, and tensor fields over 3D Euclidean space to represent data, and equivariant convolutions to map between such representations. These SE(3)-equivariant convolutions utilize kernels which are parameterized as a linear combination of a complete steerable kernel basis, which is derived analytically in this paper. We prove that equivariant convolutions are the most general equivariant linear maps between fields over R^3. Our experimental results confirm the effectiveness of 3D Steerable CNNs for the problem of amino acid propensity prediction and protein structure classification, both of which have inherent SE(3) symmetry.

A jamming transition from under- to over-parametrization affects loss landscape and generalization

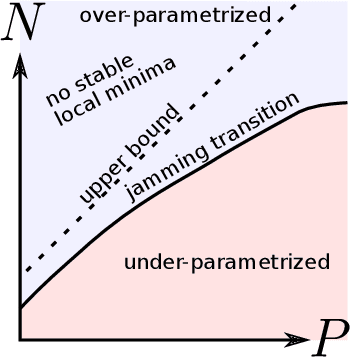
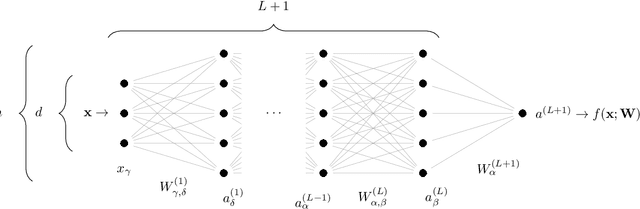
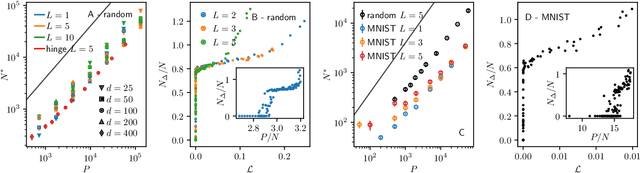
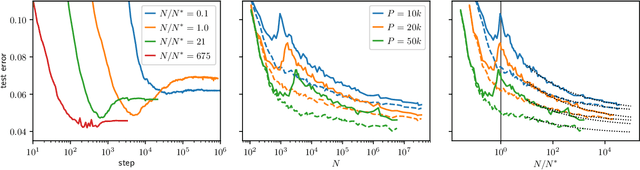
We argue that in fully-connected networks a phase transition delimits the over- and under-parametrized regimes where fitting can or cannot be achieved. Under some general conditions, we show that this transition is sharp for the hinge loss. In the whole over-parametrized regime, poor minima of the loss are not encountered during training since the number of constraints to satisfy is too small to hamper minimization. Our findings support a link between this transition and the generalization properties of the network: as we increase the number of parameters of a given model, starting from an under-parametrized network, we observe that the generalization error displays three phases: (i) initial decay, (ii) increase until the transition point --- where it displays a cusp --- and (iii) power law decay toward a constant for the rest of the over-parametrized regime. Thereby we identify the region where the classical phenomenon of over-fitting takes place, and the region where the model keeps improving, in line with previous empirical observations for modern neural networks. The theoretical results presented here appeared elsewhere for a physics audience. The results on generalization are new.

The jamming transition as a paradigm to understand the loss landscape of deep neural networks

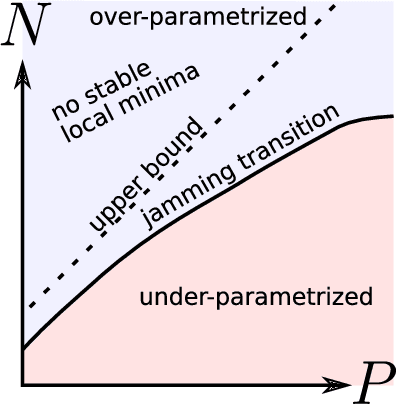
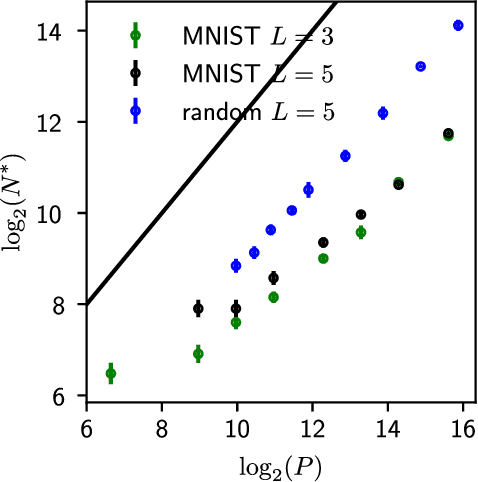
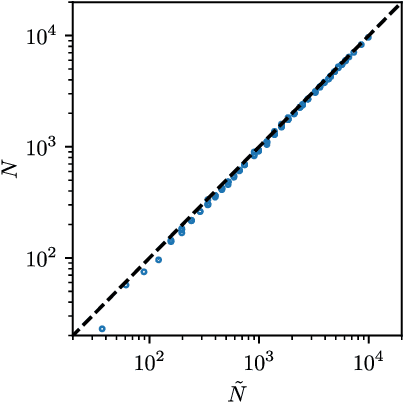
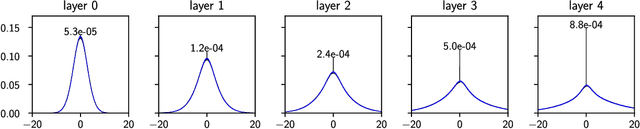
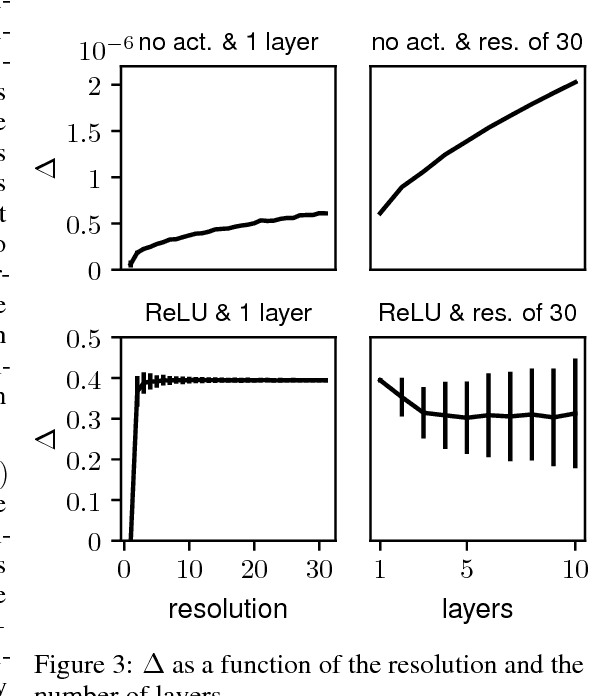
Deep learning has been immensely successful at a variety of tasks, ranging from classification to AI. Learning corresponds to fitting training data, which is implemented by descending a very high-dimensional loss function. Understanding under which conditions neural networks do not get stuck in poor minima of the loss, and how the landscape of that loss evolves as depth is increased remains a challenge. Here we predict, and test empirically, an analogy between this landscape and the energy landscape of repulsive ellipses. We argue that in FC networks a phase transition delimits the over- and under-parametrized regimes where fitting can or cannot be achieved. In the vicinity of this transition, properties of the curvature of the minima of the loss are critical. This transition shares direct similarities with the jamming transition by which particles form a disordered solid as the density is increased, which also occurs in certain classes of computational optimization and learning problems such as the perceptron. Our analysis gives a simple explanation as to why poor minima of the loss cannot be encountered in the overparametrized regime, and puts forward the surprising result that the ability of fully connected networks to fit random data is independent of their depth. Our observations suggests that this independence also holds for real data. We also study a quantity $\Delta$ which characterizes how well ($\Delta<0$) or badly ($\Delta>0$) a datum is learned. At the critical point it is power-law distributed, $P_+(\Delta)\sim\Delta^\theta$ for $\Delta>0$ and $P_-(\Delta)\sim(-\Delta)^{-\gamma}$ for $\Delta<0$, with $\theta\approx0.3$ and $\gamma\approx0.2$. This observation suggests that near the transition the loss landscape has a hierarchical structure and that the learning dynamics is prone to avalanche-like dynamics, with abrupt changes in the set of patterns that are learned.

Intertwiners between Induced Representations (with Applications to the Theory of Equivariant Neural Networks)

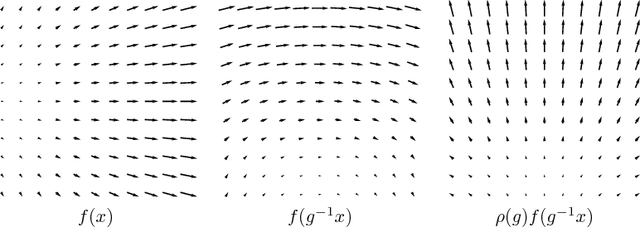
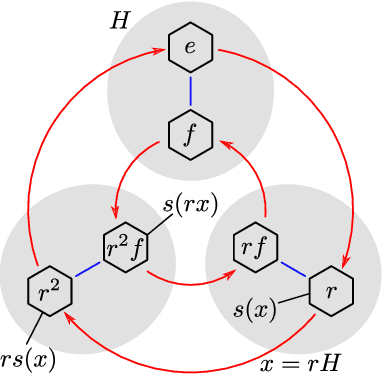
Group equivariant and steerable convolutional neural networks (regular and steerable G-CNNs) have recently emerged as a very effective model class for learning from signal data such as 2D and 3D images, video, and other data where symmetries are present. In geometrical terms, regular G-CNNs represent data in terms of scalar fields ("feature channels"), whereas the steerable G-CNN can also use vector or tensor fields ("capsules") to represent data. In algebraic terms, the feature spaces in regular G-CNNs transform according to a regular representation of the group G, whereas the feature spaces in Steerable G-CNNs transform according to the more general induced representations of G. In order to make the network equivariant, each layer in a G-CNN is required to intertwine between the induced representations associated with its input and output space. In this paper we present a general mathematical framework for G-CNNs on homogeneous spaces like Euclidean space or the sphere. We show, using elementary methods, that the layers of an equivariant network are convolutional if and only if the input and output feature spaces transform according to an induced representation. This result, which follows from G.W. Mackey's abstract theory on induced representations, establishes G-CNNs as a universal class of equivariant network architectures, and generalizes the important recent work of Kondor & Trivedi on the intertwiners between regular representations.

Spherical CNNs

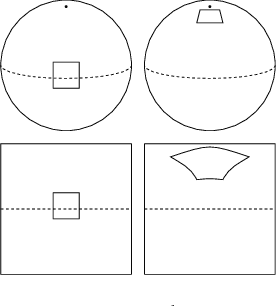
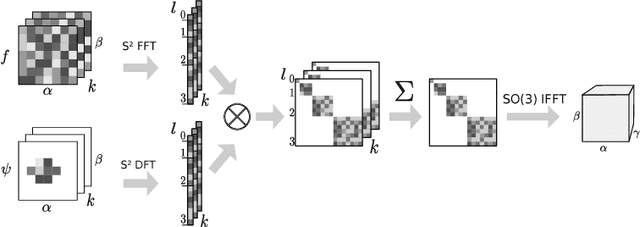
Convolutional Neural Networks (CNNs) have become the method of choice for learning problems involving 2D planar images. However, a number of problems of recent interest have created a demand for models that can analyze spherical images. Examples include omnidirectional vision for drones, robots, and autonomous cars, molecular regression problems, and global weather and climate modelling. A naive application of convolutional networks to a planar projection of the spherical signal is destined to fail, because the space-varying distortions introduced by such a projection will make translational weight sharing ineffective. In this paper we introduce the building blocks for constructing spherical CNNs. We propose a definition for the spherical cross-correlation that is both expressive and rotation-equivariant. The spherical correlation satisfies a generalized Fourier theorem, which allows us to compute it efficiently using a generalized (non-commutative) Fast Fourier Transform (FFT) algorithm. We demonstrate the computational efficiency, numerical accuracy, and effectiveness of spherical CNNs applied to 3D model recognition and atomization energy regression.

Convolutional Networks for Spherical Signals

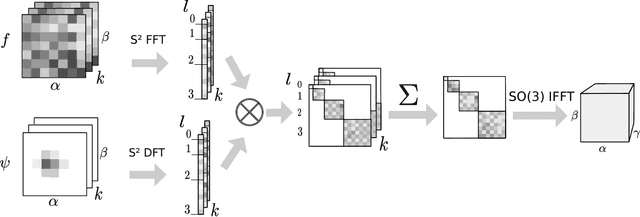
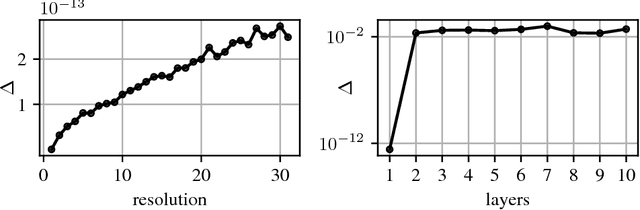
The success of convolutional networks in learning problems involving planar signals such as images is due to their ability to exploit the translation symmetry of the data distribution through weight sharing. Many areas of science and egineering deal with signals with other symmetries, such as rotation invariant data on the sphere. Examples include climate and weather science, astrophysics, and chemistry. In this paper we present spherical convolutional networks. These networks use convolutions on the sphere and rotation group, which results in rotational weight sharing and rotation equivariance. Using a synthetic spherical MNIST dataset, we show that spherical convolutional networks are very effective at dealing with rotationally invariant classification problems.