Enhancing generalizability of model discovery across parameter space with multi-experiment equation learning (ME-EQL)

Agent-based modeling (ABM) is a powerful tool for understanding self-organizing biological systems, but it is computationally intensive and often not analytically tractable. Equation learning (EQL) methods can derive continuum models from ABM data, but they typically require extensive simulations for each parameter set, raising concerns about generalizability. In this work, we extend EQL to Multi-experiment equation learning (ME-EQL) by introducing two methods: one-at-a-time ME-EQL (OAT ME-EQL), which learns individual models for each parameter set and connects them via interpolation, and embedded structure ME-EQL (ES ME-EQL), which builds a unified model library across parameters. We demonstrate these methods using a birth--death mean-field model and an on-lattice agent-based model of birth, death, and migration with spatial structure. Our results show that both methods significantly reduce the relative error in recovering parameters from agent-based simulations, with OAT ME-EQL offering better generalizability across parameter space. Our findings highlight the potential of equation learning from multiple experiments to enhance the generalizability and interpretability of learned models for complex biological systems.

Model reconstruction from temporal data for coupled oscillator networks

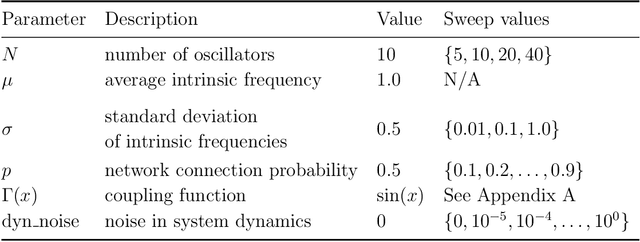
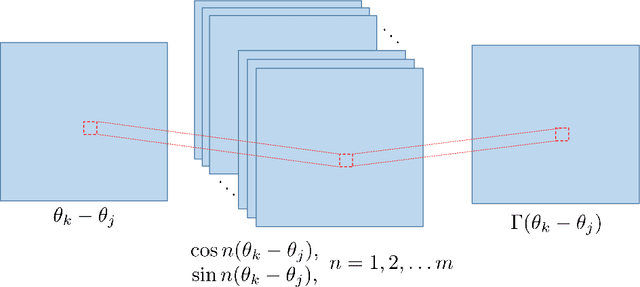
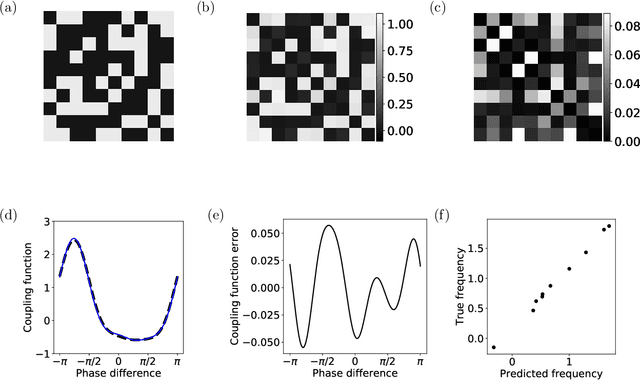
In a complex system, the interactions between individual agents often lead to emergent collective behavior like spontaneous synchronization, swarming, and pattern formation. The topology of the network of interactions can have a dramatic influence over those dynamics. In many studies, researchers start with a specific model for both the intrinsic dynamics of each agent and the interaction network, and attempt to learn about the dynamics that can be observed in the model. Here we consider the inverse problem: given the dynamics of a system, can one learn about the underlying network? We investigate arbitrary networks of coupled phase-oscillators whose dynamics are characterized by synchronization. We demonstrate that, given sufficient observational data on the transient evolution of each oscillator, one can use machine learning methods to reconstruct the interaction network and simultaneously identify the parameters of a model for the intrinsic dynamics of the oscillators and their coupling.