The Logical Expressiveness of Temporal GNNs via Two-Dimensional Product Logics

In recent years, the expressive power of various neural architectures -- including graph neural networks (GNNs), transformers, and recurrent neural networks -- has been characterised using tools from logic and formal language theory. As the capabilities of basic architectures are becoming well understood, increasing attention is turning to models that combine multiple architectural paradigms. Among them particularly important, and challenging to analyse, are temporal extensions of GNNs, which integrate both spatial (graph-structure) and temporal (evolution over time) dimensions. In this paper, we initiate the study of logical characterisation of temporal GNNs by connecting them to two-dimensional product logics. We show that the expressive power of temporal GNNs depends on how graph and temporal components are combined. In particular, temporal GNNs that apply static GNNs recursively over time can capture all properties definable in the product logic of (past) propositional temporal logic PTL and the modal logic K. In contrast, architectures such as graph-and-time TGNNs and global TGNNs can only express restricted fragments of this logic, where the interaction between temporal and spatial operators is syntactically constrained. These results yield the first logical characterisations of temporal GNNs and establish new relative expressiveness results for temporal GNNs.

NoPE: The Counting Power of Transformers with No Positional Encodings

Positional Encodings (PEs) seem to be indispensable for ensuring expressiveness of transformers; without them attention transformers reduce to a bag-of-word model. NoPE-transformers (i.e. with No PEs) with unique hard attention mechanisms were very recently shown to only be able to express regular languages, i.e., with limited counting ability. This paper shows that, with average hard attention mechanisms, NoPE-transformers are still surprisingly expressive: they can express counting languages corresponding to nonnegative integer solutions to multivariate polynomial equations (i.e. Diophantine equations), reasoning about which is well-known to be undecidable. In fact, we provide a precise characterization of languages expressible by Average Hard Attention NoPE-Transformers (NoPE-AHATs): they correspond precisely to what we call \emph{semi-algebraic sets}, i.e., finite unions of sets of nonnegative integer solutions to systems of multivariate polynomial inequations. We obtain several interesting consequences of our characterization. Firstly, NoPE-transformers can express counting properties that are far more complex than established models like simplified counter machines and Petri nets, but cannot express a very simple counting property of PARITY. Secondly, the problem of analyzing NoPE-transformers is undecidable, e.g., whether a given NoPE transformer classifies all input strings in one class. To complement our results, we exhibit a counting language that is not expressible by average hard attention transformers even with arbitrary PEs but is expressible in the circuit complexity class TC$^0$, answering an open problem.

Verifying Quantized Graph Neural Networks is PSPACE-complete

In this paper, we investigate verification of quantized Graph Neural Networks (GNNs), where some fixed-width arithmetic is used to represent numbers. We introduce the linear-constrained validity (LVP) problem for verifying GNNs properties, and provide an efficient translation from LVP instances into a logical language. We show that LVP is in PSPACE, for any reasonable activation functions. We provide a proof system. We also prove PSPACE-hardness, indicating that while reasoning about quantized GNNs is feasible, it remains generally computationally challenging.

The Computational Complexity of Formal Reasoning for Encoder-Only Transformers

We investigate challenges and possibilities of formal reasoning for encoder-only transformers (EOT), meaning sound and complete methods for verifying or interpreting behaviour. In detail, we condense related formal reasoning tasks in the form of a naturally occurring satisfiability problem (SAT). We find that SAT is undecidable if we consider EOT, commonly considered in the expressiveness community. Furthermore, we identify practical scenarios where SAT is decidable and establish corresponding complexity bounds. Besides trivial cases, we find that quantized EOT, namely those restricted by some fixed-width arithmetic, lead to the decidability of SAT due to their limited attention capabilities. However, the problem remains difficult, as we establish those scenarios where SAT is NEXPTIME-hard and those where we can show that it is solvable in NEXPTIME for quantized EOT. To complement our theoretical results, we put our findings and their implications in the overall perspective of formal reasoning.

A Logic for Reasoning About Aggregate-Combine Graph Neural Networks

We propose a modal logic in which counting modalities appear in linear inequalities. We show that each formula can be transformed into an equivalent graph neural network (GNN). We also show that a broad class of GNNs can be transformed efficiently into a formula, thus significantly improving upon the literature about the logical expressiveness of GNNs. We also show that the satisfiability problem is PSPACE-complete. These results bring together the promise of using standard logical methods for reasoning about GNNs and their properties, particularly in applications such as GNN querying, equivalence checking, etc. We prove that such natural problems can be solved in polynomial space.

Verifying And Interpreting Neural Networks using Finite Automata

Verifying properties and interpreting the behaviour of deep neural networks (DNN) is an important task given their ubiquitous use in applications, including safety-critical ones, and their blackbox nature. We propose an automata-theoric approach to tackling problems arising in DNN analysis. We show that the input-output behaviour of a DNN can be captured precisely by a (special) weak B\"uchi automaton of exponential size. We show how these can be used to address common verification and interpretation tasks like adversarial robustness, minimum sufficient reasons etc. We report on a proof-of-concept implementation translating DNN to automata on finite words for better efficiency at the cost of losing precision in analysis.

We Cannot Guarantee Safety: The Undecidability of Graph Neural Network Verification

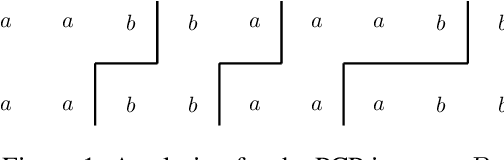
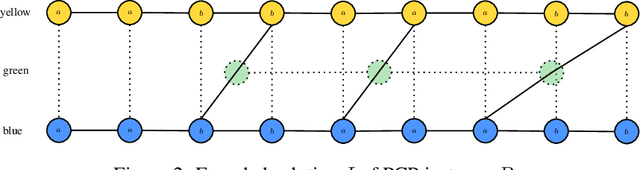
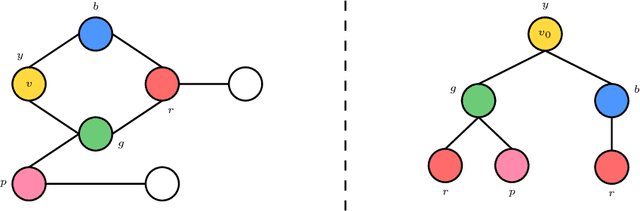
Graph Neural Networks (GNN) are commonly used for two tasks: (whole) graph classification and node classification. We formally introduce generically formulated decision problems for both tasks, corresponding to the following pattern: given a GNN, some specification of valid inputs, and some specification of valid outputs, decide whether there is a valid input satisfying the output specification. We then prove that graph classifier verification is undecidable in general, implying that there cannot be an algorithm surely guaranteeing the absence of misclassification of any kind. Additionally, we show that verification in the node classification case becomes decidable as soon as we restrict the degree of the considered graphs. Furthermore, we discuss possible changes to these results depending on the considered GNN model and specifications.

Reachability In Simple Neural Networks

We investigate the complexity of the reachability problem for (deep) neural networks: does it compute valid output given some valid input? It was recently claimed that the problem is NP-complete for general neural networks and specifications over the input/output dimension given by conjunctions of linear inequalities. We recapitulate the proof and repair some flaws in the original upper and lower bound proofs. Motivated by the general result, we show that NP-hardness already holds for restricted classes of simple specifications and neural networks. Allowing for a single hidden layer and an output dimension of one as well as neural networks with just one negative, zero and one positive weight or bias is sufficient to ensure NP-hardness. Additionally, we give a thorough discussion and outlook of possible extensions for this direction of research on neural network verification.

Reachability Is NP-Complete Even for the Simplest Neural Networks

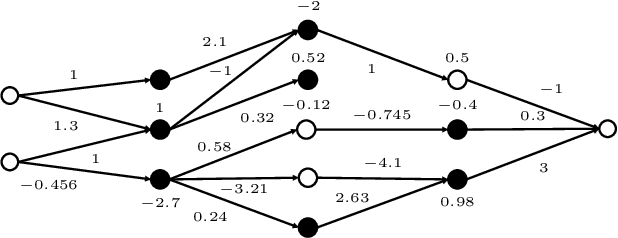
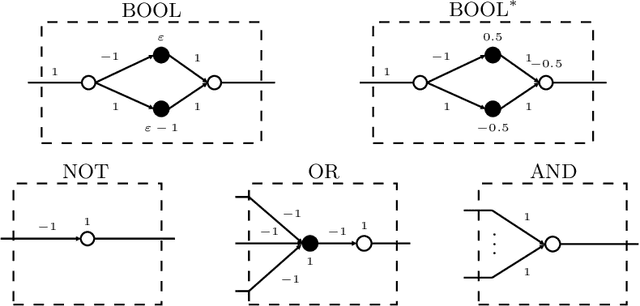
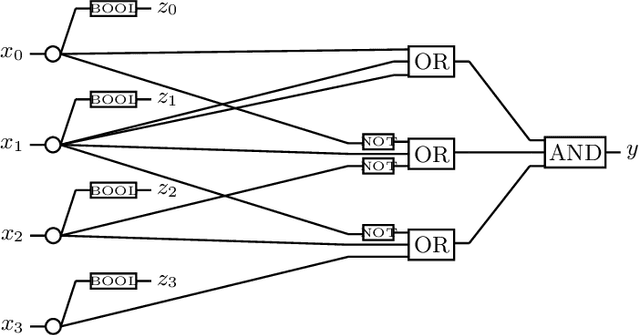
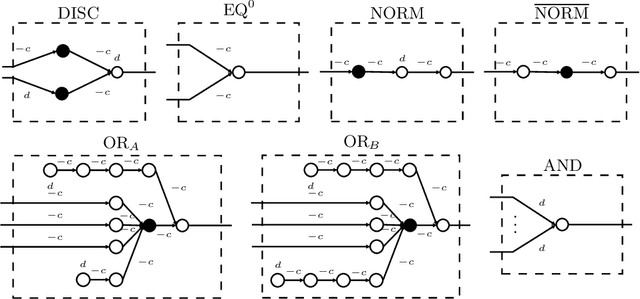
We investigate the complexity of the reachability problem for (deep) neural networks: does it compute valid output given some valid input? It was recently claimed that the problem is NP-complete for general neural networks and conjunctive input/output specifications. We repair some flaws in the original upper and lower bound proofs. We then show that NP-hardness already holds for restricted classes of simple specifications and neural networks with just one layer, as well as neural networks with minimal requirements on the occurring parameters.