Marco Bardoscia
Solving Heterogeneous General Equilibrium Economic Models with Deep Reinforcement Learning
Mar 31, 2021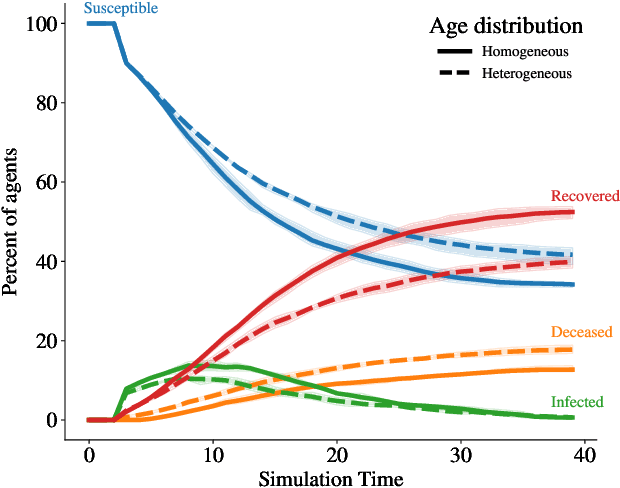
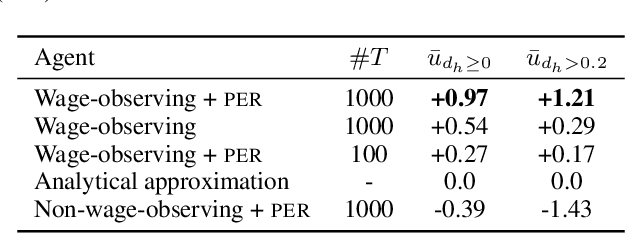
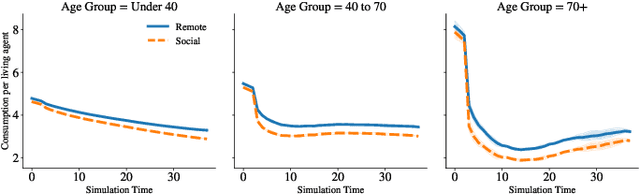
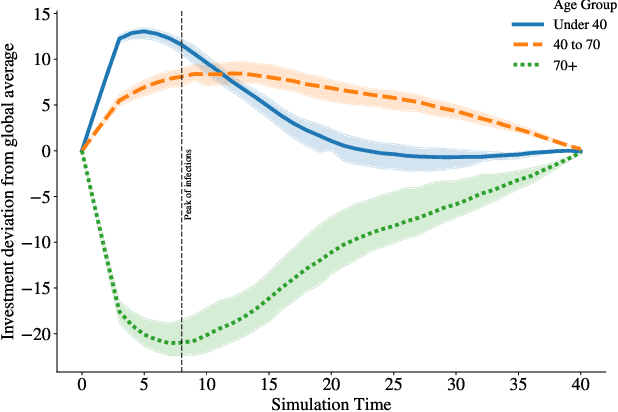
Abstract:General equilibrium macroeconomic models are a core tool used by policymakers to understand a nation's economy. They represent the economy as a collection of forward-looking actors whose behaviours combine, possibly with stochastic effects, to determine global variables (such as prices) in a dynamic equilibrium. However, standard semi-analytical techniques for solving these models make it difficult to include the important effects of heterogeneous economic actors. The COVID-19 pandemic has further highlighted the importance of heterogeneity, for example in age and sector of employment, in macroeconomic outcomes and the need for models that can more easily incorporate it. We use techniques from reinforcement learning to solve such models incorporating heterogeneous agents in a way that is simple, extensible, and computationally efficient. We demonstrate the method's accuracy and stability on a toy problem for which there is a known analytical solution, its versatility by solving a general equilibrium problem that includes global stochasticity, and its flexibility by solving a combined macroeconomic and epidemiological model to explore the economic and health implications of a pandemic. The latter successfully captures plausible economic behaviours induced by differential health risks by age.
The SAT-UNSAT transition in the adversarial SAT problem
Mar 07, 2014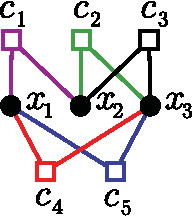
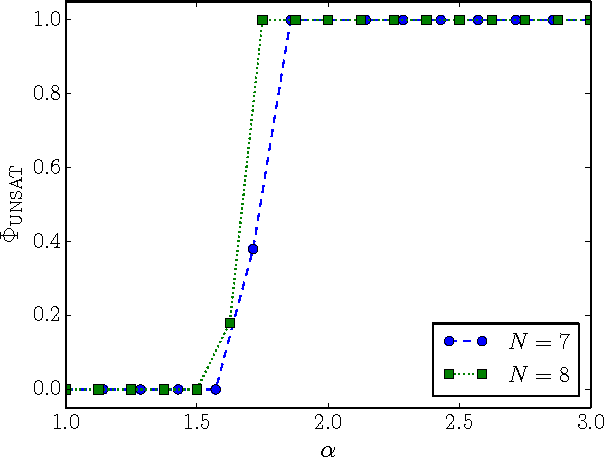
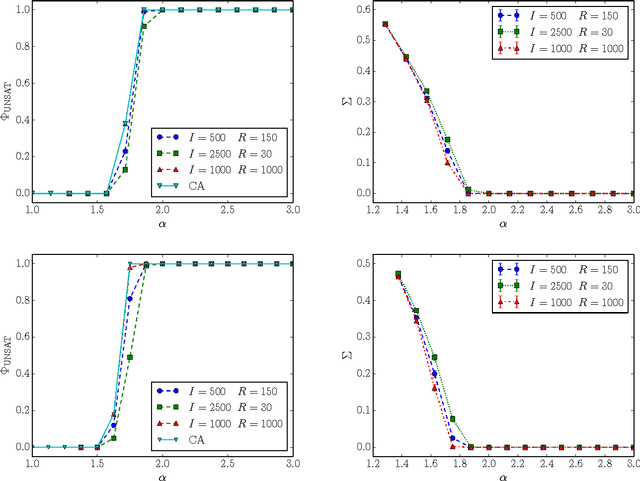
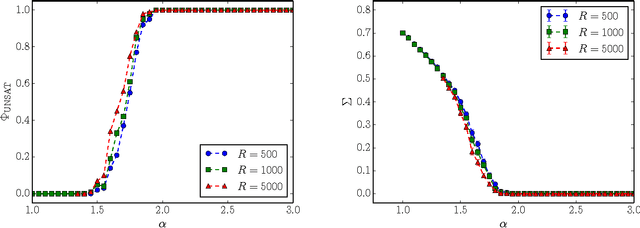
Abstract:Adversarial SAT (AdSAT) is a generalization of the satisfiability (SAT) problem in which two players try to make a boolean formula true (resp. false) by controlling their respective sets of variables. AdSAT belongs to a higher complexity class in the polynomial hierarchy than SAT and therefore the nature of the critical region and the transition are not easily paralleled to those of SAT and worth of independent study. AdSAT also provides an upper bound for the transition threshold of the quantum satisfiability problem (QSAT). We present a complete algorithm for AdSAT, show that 2-AdSAT is in $\mathbf{P}$, and then study two stochastic algorithms (simulated annealing and its improved variant) and compare their performances in detail for 3-AdSAT. Varying the density of clauses $\alpha$ we find a sharp SAT-UNSAT transition at a critical value whose upper bound is $\alpha_c \lesssim 1.5$, thus providing a much stricter upper bound for the QSAT transition than those previously found.
* 13 pages, 8 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge