The SAT-UNSAT transition in the adversarial SAT problem
Paper and Code
Mar 07, 2014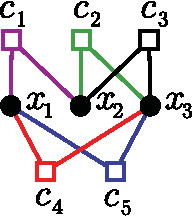
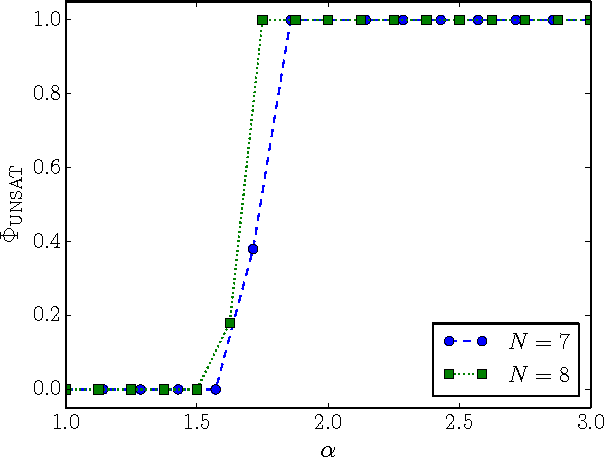
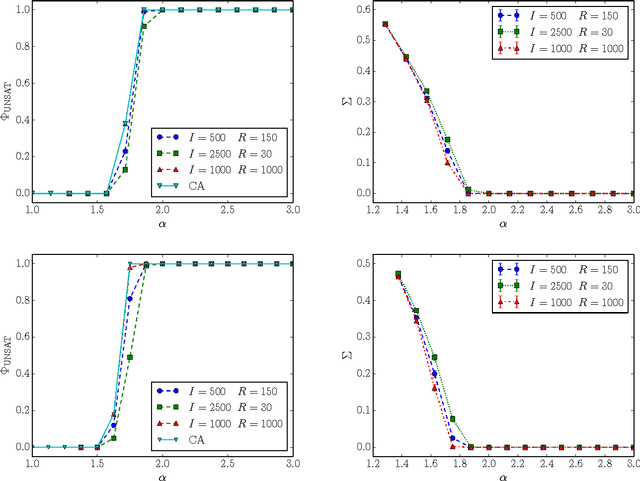
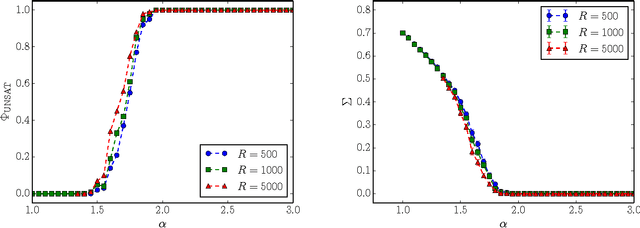
Adversarial SAT (AdSAT) is a generalization of the satisfiability (SAT) problem in which two players try to make a boolean formula true (resp. false) by controlling their respective sets of variables. AdSAT belongs to a higher complexity class in the polynomial hierarchy than SAT and therefore the nature of the critical region and the transition are not easily paralleled to those of SAT and worth of independent study. AdSAT also provides an upper bound for the transition threshold of the quantum satisfiability problem (QSAT). We present a complete algorithm for AdSAT, show that 2-AdSAT is in $\mathbf{P}$, and then study two stochastic algorithms (simulated annealing and its improved variant) and compare their performances in detail for 3-AdSAT. Varying the density of clauses $\alpha$ we find a sharp SAT-UNSAT transition at a critical value whose upper bound is $\alpha_c \lesssim 1.5$, thus providing a much stricter upper bound for the QSAT transition than those previously found.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge