Language Generation: Complexity Barriers and Implications for Learning

Kleinberg and Mullainathan showed that, in principle, language generation is always possible: with sufficiently many positive examples, a learner can eventually produce sentences indistinguishable from those of a target language. However, the existence of such a guarantee does not speak to its practical feasibility. In this work, we show that even for simple and well-studied language families -- such as regular and context-free languages -- the number of examples required for successful generation can be extraordinarily large, and in some cases not bounded by any computable function. These results reveal a substantial gap between theoretical possibility and efficient learnability. They suggest that explaining the empirical success of modern language models requires a refined perspective -- one that takes into account structural properties of natural language that make effective generation possible in practice.

Probabilistic Explanations for Linear Models

Formal XAI is an emerging field that focuses on providing explanations with mathematical guarantees for the decisions made by machine learning models. A significant amount of work in this area is centered on the computation of "sufficient reasons". Given a model $M$ and an input instance $\vec{x}$, a sufficient reason for the decision $M(\vec{x})$ is a subset $S$ of the features of $\vec{x}$ such that for any instance $\vec{z}$ that has the same values as $\vec{x}$ for every feature in $S$, it holds that $M(\vec{x}) = M(\vec{z})$. Intuitively, this means that the features in $S$ are sufficient to fully justify the classification of $\vec{x}$ by $M$. For sufficient reasons to be useful in practice, they should be as small as possible, and a natural way to reduce the size of sufficient reasons is to consider a probabilistic relaxation; the probability of $M(\vec{x}) = M(\vec{z})$ must be at least some value $\delta \in (0,1]$, for a random instance $\vec{z}$ that coincides with $\vec{x}$ on the features in $S$. Computing small $\delta$-sufficient reasons ($\delta$-SRs) is known to be a theoretically hard problem; even over decision trees--traditionally deemed simple and interpretable models--strong inapproximability results make the efficient computation of small $\delta$-SRs unlikely. We propose the notion of $(\delta, \epsilon)$-SR, a simple relaxation of $\delta$-SRs, and show that this kind of explanation can be computed efficiently over linear models.

Restructuring Tractable Probabilistic Circuits

Probabilistic circuits (PCs) is a unifying representation for probabilistic models that support tractable inference. Numerous applications of PCs like controllable text generation depend on the ability to efficiently multiply two circuits. Existing multiplication algorithms require that the circuits respect the same structure, i.e. variable scopes decomposes according to the same vtree. In this work, we propose and study the task of restructuring structured(-decomposable) PCs, that is, transforming a structured PC such that it conforms to a target vtree. We propose a generic approach for this problem and show that it leads to novel polynomial-time algorithms for multiplying circuits respecting different vtrees, as well as a practical depth-reduction algorithm that preserves structured decomposibility. Our work opens up new avenues for tractable PC inference, suggesting the possibility of training with less restrictive PC structures while enabling efficient inference by changing their structures at inference time.

A Symbolic Language for Interpreting Decision Trees

The recent development of formal explainable AI has disputed the folklore claim that "decision trees are readily interpretable models", showing different interpretability queries that are computationally hard on decision trees, as well as proposing different methods to deal with them in practice. Nonetheless, no single explainability query or score works as a "silver bullet" that is appropriate for every context and end-user. This naturally suggests the possibility of "interpretability languages" in which a wide variety of queries can be expressed, giving control to the end-user to tailor queries to their particular needs. In this context, our work presents ExplainDT, a symbolic language for interpreting decision trees. ExplainDT is rooted in a carefully constructed fragment of first-ordered logic that we call StratiFOILed. StratiFOILed balances expressiveness and complexity of evaluation, allowing for the computation of many post-hoc explanations--both local (e.g., abductive and contrastive explanations) and global ones (e.g., feature relevancy)--while remaining in the Boolean Hierarchy over NP. Furthermore, StratiFOILed queries can be written as a Boolean combination of NP-problems, thus allowing us to evaluate them in practice with a constant number of calls to a SAT solver. On the theoretical side, our main contribution is an in-depth analysis of the expressiveness and complexity of StratiFOILed, while on the practical side, we provide an optimized implementation for encoding StratiFOILed queries as propositional formulas, together with an experimental study on its efficiency.

Foundations of Symbolic Languages for Model Interpretability

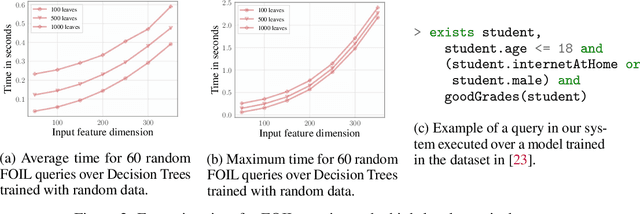
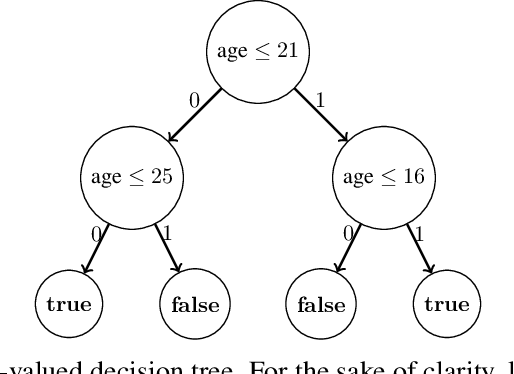
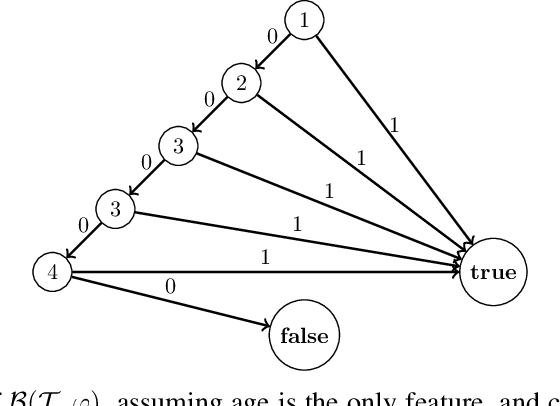
Several queries and scores have recently been proposed to explain individual predictions over ML models. Given the need for flexible, reliable, and easy-to-apply interpretability methods for ML models, we foresee the need for developing declarative languages to naturally specify different explainability queries. We do this in a principled way by rooting such a language in a logic, called FOIL, that allows for expressing many simple but important explainability queries, and might serve as a core for more expressive interpretability languages. We study the computational complexity of FOIL queries over two classes of ML models often deemed to be easily interpretable: decision trees and OBDDs. Since the number of possible inputs for an ML model is exponential in its dimension, the tractability of the FOIL evaluation problem is delicate but can be achieved by either restricting the structure of the models or the fragment of FOIL being evaluated. We also present a prototype implementation of FOIL wrapped in a high-level declarative language and perform experiments showing that such a language can be used in practice.

Querying in the Age of Graph Databases and Knowledge Graphs

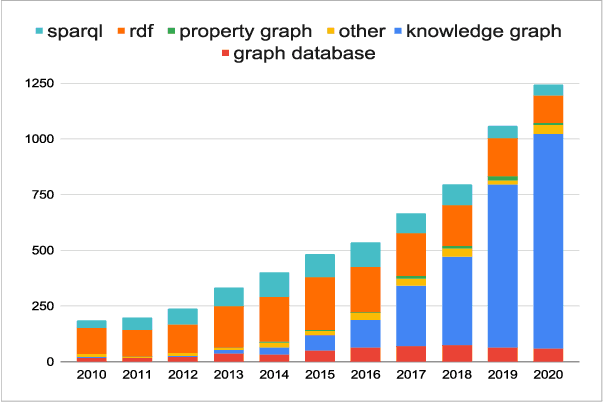
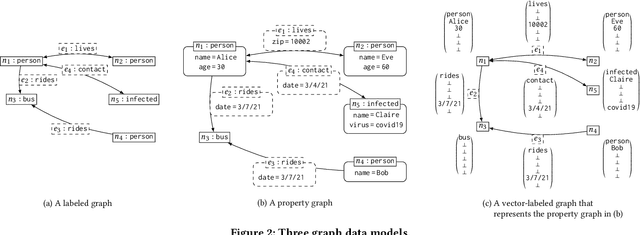
Graphs have become the best way we know of representing knowledge. The computing community has investigated and developed the support for managing graphs by means of digital technology. Graph databases and knowledge graphs surface as the most successful solutions to this program. The goal of this document is to provide a conceptual map of the data management tasks underlying these developments, paying particular attention to data models and query languages for graphs.

On the Complexity of SHAP-Score-Based Explanations: Tractability via Knowledge Compilation and Non-Approximability Results

In Machine Learning, the $\mathsf{SHAP}$-score is a version of the Shapley value that is used to explain the result of a learned model on a specific entity by assigning a score to every feature. While in general computing Shapley values is an intractable problem, we prove a strong positive result stating that the $\mathsf{SHAP}$-score can be computed in polynomial time over deterministic and decomposable Boolean circuits. Such circuits are studied in the field of Knowledge Compilation and generalize a wide range of Boolean circuits and binary decision diagrams classes, including binary decision trees and Ordered Binary Decision Diagrams (OBDDs). We also establish the computational limits of the SHAP-score by observing that computing it over a class of Boolean models is always polynomially as hard as the model counting problem for that class. This implies that both determinism and decomposability are essential properties for the circuits that we consider. It also implies that computing $\mathsf{SHAP}$-scores is intractable as well over the class of propositional formulas in DNF. Based on this negative result, we look for the existence of fully-polynomial randomized approximation schemes (FPRAS) for computing $\mathsf{SHAP}$-scores over such class. In contrast to the model counting problem for DNF formulas, which admits an FPRAS, we prove that no such FPRAS exists for the computation of $\mathsf{SHAP}$-scores. Surprisingly, this negative result holds even for the class of monotone formulas in DNF. These techniques can be further extended to prove another strong negative result: Under widely believed complexity assumptions, there is no polynomial-time algorithm that checks, given a monotone DNF formula $\varphi$ and features $x,y$, whether the $\mathsf{SHAP}$-score of $x$ in $\varphi$ is smaller than the $\mathsf{SHAP}$-score of $y$ in $\varphi$.

The Tractability of SHAP-scores over Deterministic and Decomposable Boolean Circuits

Scores based on Shapley values are currently widely used for providing explanations to classification results over machine learning models. A prime example of this corresponds to the influential SHAP-score, a version of the Shapley value in which the contribution of a set $S$ of features from a given entity $\mathbf{e}$ over a model $M$ is defined as the expected value in $M$ of the set of entities $\mathbf{e}'$ that coincide with $\mathbf{e}$ over all features in $S$. While in general computing Shapley values is a computationally intractable problem, it has recently been claimed that the SHAP-score can be computed in polynomial time over the class of decision trees. In this paper, we provide a proof of a stronger result over Boolean models: the SHAP-score can be computed in polynomial time over deterministic and decomposable Boolean circuits, also known as tractable probabilistic circuits. Such circuits encompass a wide range of Boolean circuits and binary decision diagrams classes, including binary decision trees and Ordered Binary Decision Diagrams (OBDDs). Moreover, we establish the computational limits of the notion of SHAP-score by showing that computing it over a class of Boolean models is always (polynomially) as hard as the model counting problem for this class (under some mild condition). This implies, for instance, that computing the SHAP-score for DNF propositional formulae is a #P-hard problem, and, thus, that determinism is essential for the circuits that we consider.

Exchanging OWL 2 QL Knowledge Bases

Knowledge base exchange is an important problem in the area of data exchange and knowledge representation, where one is interested in exchanging information between a source and a target knowledge base connected through a mapping. In this paper, we study this fundamental problem for knowledge bases and mappings expressed in OWL 2 QL, the profile of OWL 2 based on the description logic DL-Lite_R. More specifically, we consider the problem of computing universal solutions, identified as one of the most desirable translations to be materialized, and the problem of computing UCQ-representations, which optimally capture in a target TBox the information that can be extracted from a source TBox and a mapping by means of unions of conjunctive queries. For the former we provide a novel automata-theoretic technique, and complexity results that range from NP to EXPTIME, while for the latter we show NLOGSPACE-completeness.