CoE: Deep Coupled Embedding for Non-Rigid Point Cloud Correspondences

The interest in matching non-rigidly deformed shapes represented as raw point clouds is rising due to the proliferation of low-cost 3D sensors. Yet, the task is challenging since point clouds are irregular and there is a lack of intrinsic shape information. We propose to tackle these challenges by learning a new shape representation -- a per-point high dimensional embedding, in an embedding space where semantically similar points share similar embeddings. The learned embedding has multiple beneficial properties: it is aware of the underlying shape geometry and is robust to shape deformations and various shape artefacts, such as noise and partiality. Consequently, this embedding can be directly employed to retrieve high-quality dense correspondences through a simple nearest neighbor search in the embedding space. Extensive experiments demonstrate new state-of-the-art results and robustness in numerous challenging non-rigid shape matching benchmarks and show its great potential in other shape analysis tasks, such as segmentation.

Beyond Complete Shapes: A quantitative Evaluation of 3D Shape Matching Algorithms

Finding correspondences between 3D shapes is an important and long-standing problem in computer vision, graphics and beyond. While approaches based on machine learning dominate modern 3D shape matching, almost all existing (learning-based) methods require that at least one of the involved shapes is complete. In contrast, the most challenging and arguably most practically relevant setting of matching partially observed shapes, is currently underexplored. One important factor is that existing datasets contain only a small number of shapes (typically below 100), which are unable to serve data-hungry machine learning approaches, particularly in the unsupervised regime. In addition, the type of partiality present in existing datasets is often artificial and far from realistic. To address these limitations and to encourage research on these relevant settings, we provide a generic and flexible framework for the procedural generation of challenging partial shape matching scenarios. Our framework allows for a virtually infinite generation of partial shape matching instances from a finite set of shapes with complete geometry. Further, we manually create cross-dataset correspondences between seven existing (complete geometry) shape matching datasets, leading to a total of 2543 shapes. Based on this, we propose several challenging partial benchmark settings, for which we evaluate respective state-of-the-art methods as baselines.

Partial-to-Partial Shape Matching with Geometric Consistency

Finding correspondences between 3D shapes is an important and long-standing problem in computer vision, graphics and beyond. A prominent challenge are partial-to-partial shape matching settings, which occur when the shapes to match are only observed incompletely (e.g. from 3D scanning). Although partial-to-partial matching is a highly relevant setting in practice, it is rarely explored. Our work bridges the gap between existing (rather artificial) 3D full shape matching and partial-to-partial real-world settings by exploiting geometric consistency as a strong constraint. We demonstrate that it is indeed possible to solve this challenging problem in a variety of settings. For the first time, we achieve geometric consistency for partial-to-partial matching, which is realized by a novel integer non-linear program formalism building on triangle product spaces, along with a new pruning algorithm based on linear integer programming. Further, we generate a new inter-class dataset for partial-to-partial shape-matching. We show that our method outperforms current SOTA methods on both an established intra-class dataset and our novel inter-class dataset.

Finsler-Laplace-Beltrami Operators with Application to Shape Analysis

The Laplace-Beltrami operator (LBO) emerges from studying manifolds equipped with a Riemannian metric. It is often called the Swiss army knife of geometry processing as it allows to capture intrinsic shape information and gives rise to heat diffusion, geodesic distances, and a multitude of shape descriptors. It also plays a central role in geometric deep learning. In this work, we explore Finsler manifolds as a generalization of Riemannian manifolds. We revisit the Finsler heat equation and derive a Finsler heat kernel and a Finsler-Laplace-Beltrami Operator (FLBO): a novel theoretically justified anisotropic Laplace-Beltrami operator (ALBO). In experimental evaluations we demonstrate that the proposed FLBO is a valuable alternative to the traditional Riemannian-based LBO and ALBOs for spatial filtering and shape correspondence estimation. We hope that the proposed Finsler heat kernel and the FLBO will inspire further exploration of Finsler geometry in the computer vision community.

Geometrically Consistent Partial Shape Matching

Finding correspondences between 3D shapes is a crucial problem in computer vision and graphics, which is for example relevant for tasks like shape interpolation, pose transfer, or texture transfer. An often neglected but essential property of matchings is geometric consistency, which means that neighboring triangles in one shape are consistently matched to neighboring triangles in the other shape. Moreover, while in practice one often has only access to partial observations of a 3D shape (e.g. due to occlusion, or scanning artifacts), there do not exist any methods that directly address geometrically consistent partial shape matching. In this work we fill this gap by proposing to integrate state-of-the-art deep shape features into a novel integer linear programming partial shape matching formulation. Our optimization yields a globally optimal solution on low resolution shapes, which we then refine using a coarse-to-fine scheme. We show that our method can find more reliable results on partial shapes in comparison to existing geometrically consistent algorithms (for which one first has to fill missing parts with a dummy geometry). Moreover, our matchings are substantially smoother than learning-based state-of-the-art shape matching methods.

SIGMA: Scale-Invariant Global Sparse Shape Matching

We propose a novel mixed-integer programming (MIP) formulation for generating precise sparse correspondences for highly non-rigid shapes. To this end, we introduce a projected Laplace-Beltrami operator (PLBO) which combines intrinsic and extrinsic geometric information to measure the deformation quality induced by predicted correspondences. We integrate the PLBO, together with an orientation-aware regulariser, into a novel MIP formulation that can be solved to global optimality for many practical problems. In contrast to previous methods, our approach is provably invariant to rigid transformations and global scaling, initialisation-free, has optimality guarantees, and scales to high resolution meshes with (empirically observed) linear time. We show state-of-the-art results for sparse non-rigid matching on several challenging 3D datasets, including data with inconsistent meshing, as well as applications in mesh-to-point-cloud matching.

Weight-Aware Implicit Geometry Reconstruction with Curvature-Guided Sampling

Neural surface implicit representations offer numerous advantages, including the ability to easily modify topology and surface resolution. However, reconstructing implicit geometry representation with only limited known data is challenging. In this paper, we present an approach that effectively interpolates and extrapolates within training points, generating additional training data to reconstruct a surface with superior qualitative and quantitative results. We also introduce a technique that efficiently calculates differentiable geometric properties, i.e., mean and Gaussian curvatures, to enhance the sampling process during training. Additionally, we propose a weight-aware implicit neural representation that not only streamlines surface extraction but also extend to non-closed surfaces by depicting non-closed areas as locally degenerated patches, thereby mitigating the drawbacks of the previous assumption in implicit neural representations.

Isometric Multi-Shape Matching

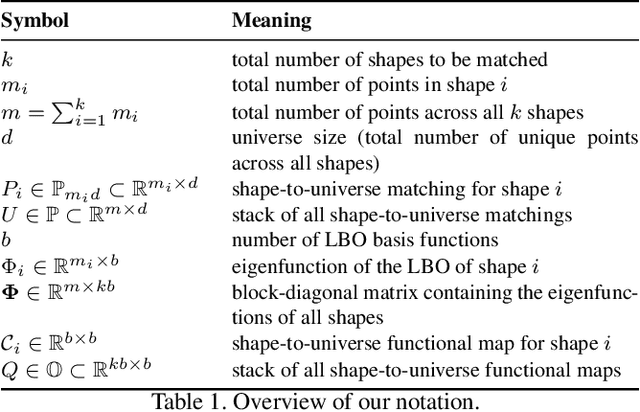
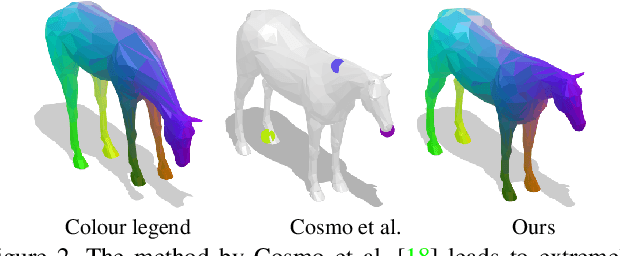
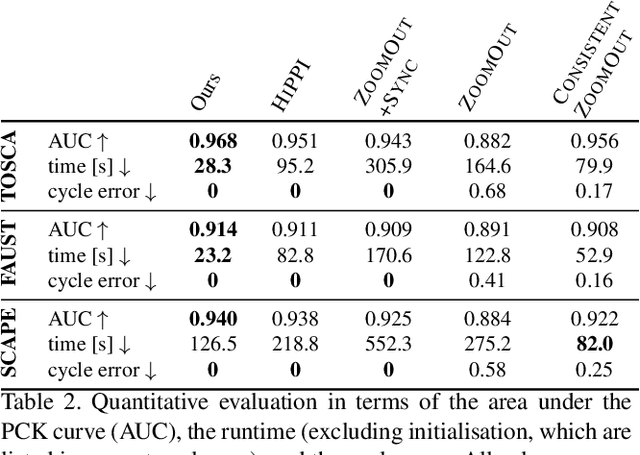
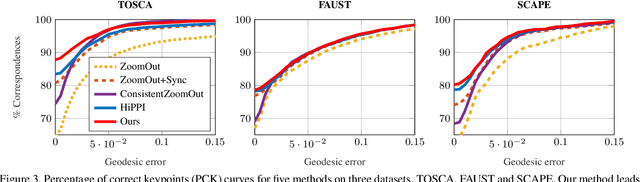
Finding correspondences between shapes is a fundamental problem in computer vision and graphics, which is relevant for many applications, including 3D reconstruction, object tracking, and style transfer. The vast majority of correspondence methods aim to find a solution between pairs of shapes, even if multiple instances of the same class are available. While isometries are often studied in shape correspondence problems, they have not been considered explicitly in the multi-matching setting. This paper closes this gap by proposing a novel optimisation formulation for isometric multi-shape matching. We present a suitable optimisation algorithm for solving our formulation and provide a convergence and complexity analysis. Our algorithm obtains multi-matchings that are by construction provably cycle-consistent. We demonstrate the superior performance of our method on various datasets and set the new state-of-the-art in isometric multi-shape matching.

Variational Uncalibrated Photometric Stereo under General Lighting

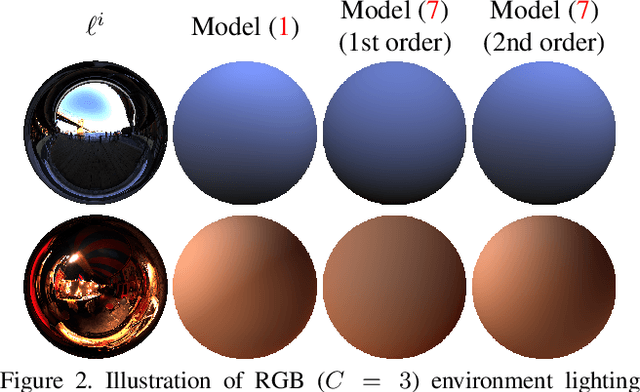
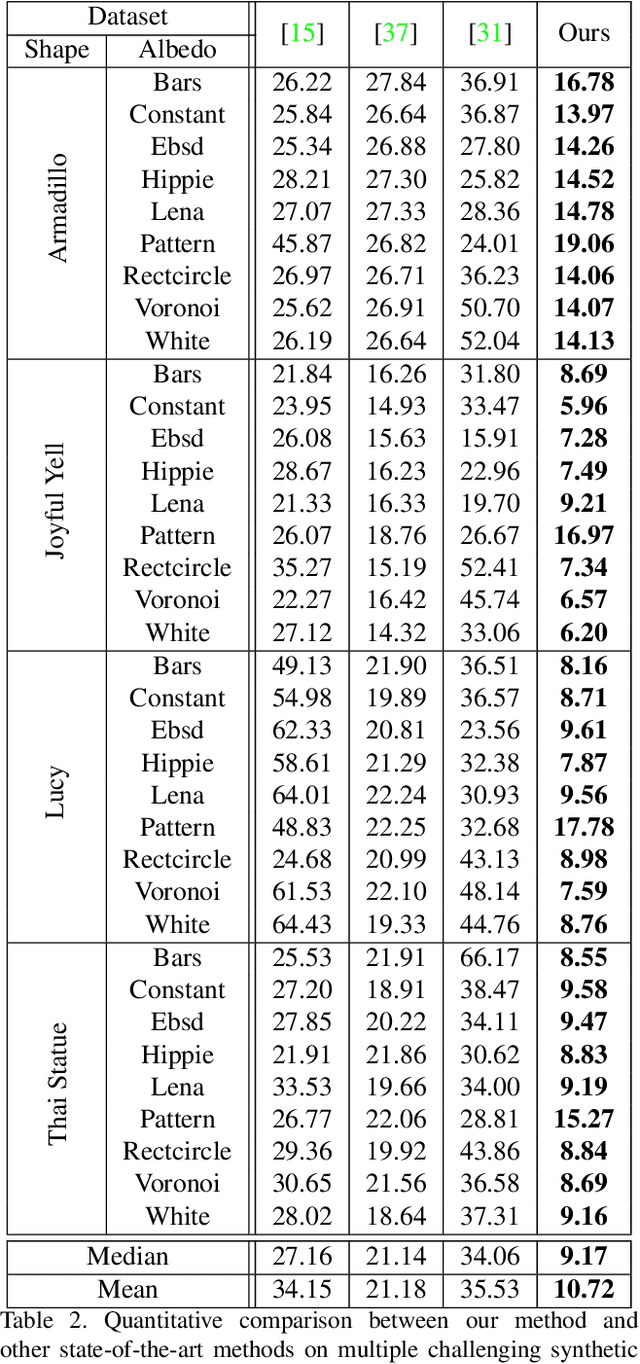
Photometric stereo (PS) techniques nowadays remain constrained to an ideal laboratory setup where modeling and calibration of lighting is amenable. This work aims to eliminate such restrictions. To this end, we introduce an efficient principled variational approach to uncalibrated PS under general illumination, which is approximated through a second-order spherical harmonic expansion. The joint recovery of shape, reflectance and illumination is formulated as a variational problem where shape estimation is carried out directly in terms of the underlying perspective depth map, thus implicitly ensuring integrability and bypassing the need for a subsequent normal integration. We provide a tailored numerical scheme to solve the resulting nonconvex problem efficiently and robustly. On a variety of evaluations, our method consistently reduces the mean angular error by a factor of 2-3 compared to the state-of-the-art.