Estimating Dense-Packed Zone Height in Liquid-Liquid Separation: A Physics-Informed Neural Network Approach

Separating liquid-liquid dispersions in gravity settlers is critical in chemical, pharmaceutical, and recycling processes. The dense-packed zone height is an important performance and safety indicator but it is often expensive and impractical to measure due to optical limitations. We propose to estimate phase heights using only inexpensive volume flow measurements. To this end, a physics-informed neural network (PINN) is first pretrained on synthetic data and physics equations derived from a low-fidelity (approximate) mechanistic model to reduce the need for extensive experimental data. While the mechanistic model is used to generate synthetic training data, only volume balance equations are used in the PINN, since the integration of submodels describing droplet coalescence and sedimentation into the PINN would be computationally prohibitive. The pretrained PINN is then fine-tuned with scarce experimental data to capture the actual dynamics of the separator. We then employ the differentiable PINN as a predictive model in an Extended Kalman Filter inspired state estimation framework, enabling the phase heights to be tracked and updated from flow-rate measurements. We first test the two-stage trained PINN by forward simulation from a known initial state against the mechanistic model and a non-pretrained PINN. We then evaluate phase height estimation performance with the filter, comparing the two-stage trained PINN with a two-stage trained purely data-driven neural network. All model types are trained and evaluated using ensembles to account for model parameter uncertainty. In all evaluations, the two-stage trained PINN yields the most accurate phase-height estimates.

Data-Driven Conditional Flexibility Index

With the increasing flexibilization of processes, determining robust scheduling decisions has become an important goal. Traditionally, the flexibility index has been used to identify safe operating schedules by approximating the admissible uncertainty region using simple admissible uncertainty sets, such as hypercubes. Presently, available contextual information, such as forecasts, has not been considered to define the admissible uncertainty set when determining the flexibility index. We propose the conditional flexibility index (CFI), which extends the traditional flexibility index in two ways: by learning the parametrized admissible uncertainty set from historical data and by using contextual information to make the admissible uncertainty set conditional. This is achieved using a normalizing flow that learns a bijective mapping from a Gaussian base distribution to the data distribution. The admissible latent uncertainty set is constructed as a hypersphere in the latent space and mapped to the data space. By incorporating contextual information, the CFI provides a more informative estimate of flexibility by defining admissible uncertainty sets in regions that are more likely to be relevant under given conditions. Using an illustrative example, we show that no general statement can be made about data-driven admissible uncertainty sets outperforming simple sets, or conditional sets outperforming unconditional ones. However, both data-driven and conditional admissible uncertainty sets ensure that only regions of the uncertain parameter space containing realizations are considered. We apply the CFI to a security-constrained unit commitment example and demonstrate that the CFI can improve scheduling quality by incorporating temporal information.

Physics-Informed Neural Networks for Dynamic Process Operations with Limited Physical Knowledge and Data

In chemical engineering, process data is often expensive to acquire, and complex phenomena are difficult to model rigorously, rendering both entirely data-driven and purely mechanistic modeling approaches impractical. We explore using physics-informed neural networks (PINNs) for modeling dynamic processes governed by differential-algebraic equation systems when process data is scarce and complete mechanistic knowledge is missing. In particular, we focus on estimating states for which neither direct observational data nor constitutive equations are available. For demonstration purposes, we study a continuously stirred tank reactor and a liquid-liquid separator. We find that PINNs can infer unmeasured states with reasonable accuracy, and they generalize better in low-data scenarios than purely data-driven models. We thus show that PINNs, similar to hybrid mechanistic/data-driven models, are capable of modeling processes when relatively few experimental data and only partially known mechanistic descriptions are available, and conclude that they constitute a promising avenue that warrants further investigation.

Task-optimal data-driven surrogate models for eNMPC via differentiable simulation and optimization

We present a method for end-to-end learning of Koopman surrogate models for optimal performance in control. In contrast to previous contributions that employ standard reinforcement learning (RL) algorithms, we use a training algorithm that exploits the potential differentiability of environments based on mechanistic simulation models. We evaluate the performance of our method by comparing it to that of other controller type and training algorithm combinations on a literature known eNMPC case study. Our method exhibits superior performance on this problem, thereby constituting a promising avenue towards more capable controllers that employ dynamic surrogate models.

Multivariate Scenario Generation of Day-Ahead Electricity Prices using Normalizing Flows

Trading on electricity markets requires accurate information about the realization of electricity prices and the uncertainty attached to the predictions. We present a probabilistic forecasting approach for day-ahead electricity prices using the fully data-driven deep generative model called normalizing flows. Our modeling approach generates full-day scenarios of day-ahead electricity prices based on conditional features such as residual load forecasts. Furthermore, we propose extended feature sets of prior realizations and a periodic retraining scheme that allows the normalizing flow to adapt to the changing conditions of modern electricity markets. In particular, we investigate the impact of the energy crisis ensuing from the Russian invasion of Ukraine. Our results highlight that the normalizing flow generates high-quality scenarios that reproduce the true price distribution and yield highly accurate forecasts. Additionally, our analysis highlights how our improvements towards adaptations in changing regimes allow the normalizing flow to adapt to changing market conditions and enables continued sampling of high-quality day-ahead price scenarios.

End-to-End Reinforcement Learning of Koopman Models for Economic Nonlinear MPC

(Economic) nonlinear model predictive control ((e)NMPC) requires dynamic system models that are sufficiently accurate in all relevant state-space regions. These models must also be computationally cheap enough to ensure real-time tractability. Data-driven surrogate models for mechanistic models can be used to reduce the computational burden of (e)NMPC; however, such models are typically trained by system identification for maximum average prediction accuracy on simulation samples and perform suboptimally as part of actual (e)NMPC. We present a method for end-to-end reinforcement learning of dynamic surrogate models for optimal performance in (e)NMPC applications, resulting in predictive controllers that strike a favorable balance between control performance and computational demand. We validate our method on two applications derived from an established nonlinear continuous stirred-tank reactor model. We compare the controller performance to that of MPCs utilizing models trained by the prevailing maximum prediction accuracy paradigm, and model-free neural network controllers trained using reinforcement learning. We show that our method matches the performance of the model-free neural network controllers while consistently outperforming models derived from system identification. Additionally, we show that the MPC policies can react to changes in the control setting without retraining.

A Recursively Recurrent Neural Network (R2N2) Architecture for Learning Iterative Algorithms

Meta-learning of numerical algorithms for a given task consist of the data-driven identification and adaptation of an algorithmic structure and the associated hyperparameters. To limit the complexity of the meta-learning problem, neural architectures with a certain inductive bias towards favorable algorithmic structures can, and should, be used. We generalize our previously introduced Runge-Kutta neural network to a recursively recurrent neural network (R2N2) superstructure for the design of customized iterative algorithms. In contrast to off-the-shelf deep learning approaches, it features a distinct division into modules for generation of information and for the subsequent assembly of this information towards a solution. Local information in the form of a subspace is generated by subordinate, inner, iterations of recurrent function evaluations starting at the current outer iterate. The update to the next outer iterate is computed as a linear combination of these evaluations, reducing the residual in this space, and constitutes the output of the network. We demonstrate that regular training of the weight parameters inside the proposed superstructure on input/output data of various computational problem classes yields iterations similar to Krylov solvers for linear equation systems, Newton-Krylov solvers for nonlinear equation systems, and Runge-Kutta integrators for ordinary differential equations. Due to its modularity, the superstructure can be readily extended with functionalities needed to represent more general classes of iterative algorithms traditionally based on Taylor series expansions.

Physical Pooling Functions in Graph Neural Networks for Molecular Property Prediction

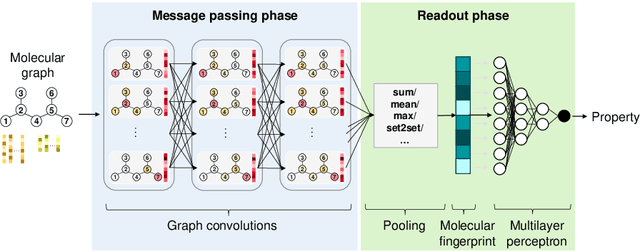
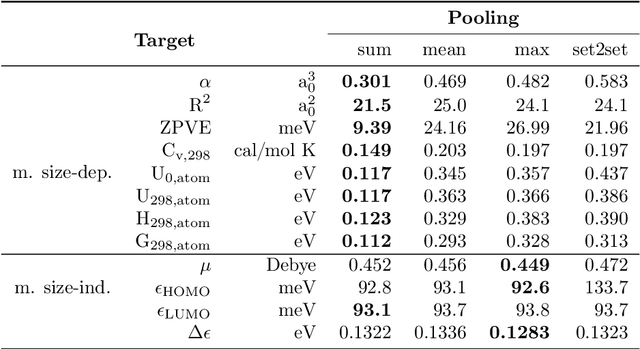
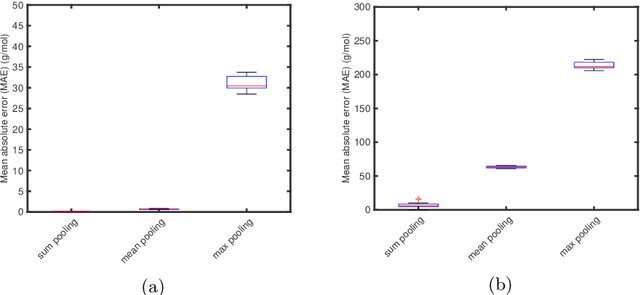
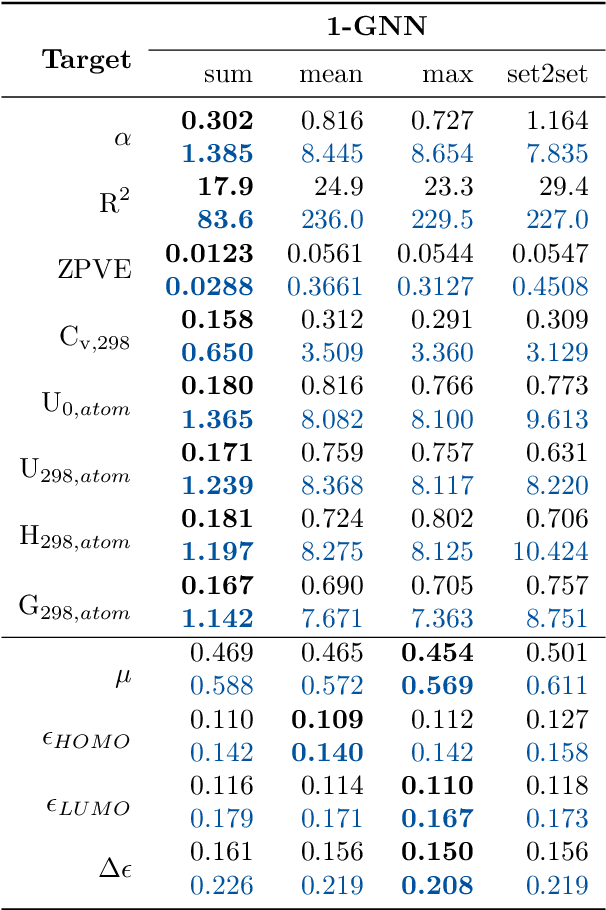
Graph neural networks (GNNs) are emerging in chemical engineering for the end-to-end learning of physicochemical properties based on molecular graphs. A key element of GNNs is the pooling function which combines atom feature vectors into molecular fingerprints. Most previous works use a standard pooling function to predict a variety of properties. However, unsuitable pooling functions can lead to unphysical GNNs that poorly generalize. We compare and select meaningful GNN pooling methods based on physical knowledge about the learned properties. The impact of physical pooling functions is demonstrated with molecular properties calculated from quantum mechanical computations. We also compare our results to the recent set2set pooling approach. We recommend using sum pooling for the prediction of properties that depend on molecular size and compare pooling functions for properties that are molecular size-independent. Overall, we show that the use of physical pooling functions significantly enhances generalization.

Graph neural networks for the prediction of molecular structure-property relationships

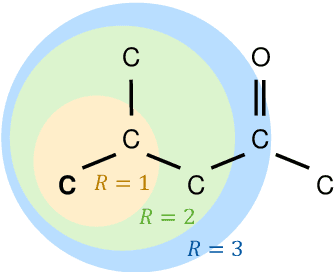
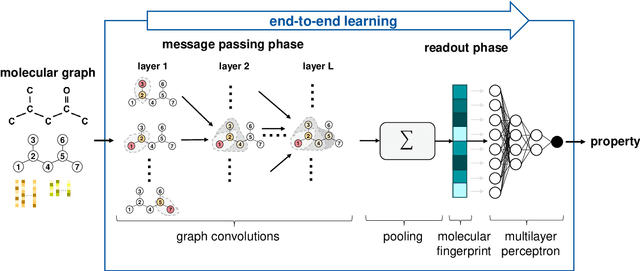
Molecular property prediction is of crucial importance in many disciplines such as drug discovery, molecular biology, or material and process design. The frequently employed quantitative structure-property/activity relationships (QSPRs/QSARs) characterize molecules by descriptors which are then mapped to the properties of interest via a linear or nonlinear model. In contrast, graph neural networks, a novel machine learning method, directly work on the molecular graph, i.e., a graph representation where atoms correspond to nodes and bonds correspond to edges. GNNs allow to learn properties in an end-to-end fashion, thereby avoiding the need for informative descriptors as in QSPRs/QSARs. GNNs have been shown to achieve state-of-the-art prediction performance on various property predictions tasks and represent an active field of research. We describe the fundamentals of GNNs and demonstrate the application of GNNs via two examples for molecular property prediction.

Graph Neural Networks for Temperature-Dependent Activity Coefficient Prediction of Solutes in Ionic Liquids

Ionic liquids (ILs) are important solvents for sustainable processes and predicting activity coefficients (ACs) of solutes in ILs is needed. Recently, matrix completion methods (MCMs), transformers, and graph neural networks (GNNs) have shown high accuracy in predicting ACs of binary mixtures, superior to well-established models, e.g., COSMO-RS and UNIFAC. GNNs are particularly promising here as they learn a molecular graph-to-property relationship without pretraining, typically required for transformers, and are, unlike MCMs, applicable to molecules not included in training. For ILs, however, GNN applications are currently missing. Herein, we present a GNN to predict temperature-dependent infinite dilution ACs of solutes in ILs. We train the GNN on a database including more than 40,000 AC values and compare it to a state-of-the-art MCM. The GNN and MCM achieve similar high prediction performance, with the GNN additionally enabling high-quality predictions for ACs of solutions that contain ILs and solutes not considered during training.