Estimating Dense-Packed Zone Height in Liquid-Liquid Separation: A Physics-Informed Neural Network Approach

Separating liquid-liquid dispersions in gravity settlers is critical in chemical, pharmaceutical, and recycling processes. The dense-packed zone height is an important performance and safety indicator but it is often expensive and impractical to measure due to optical limitations. We propose to estimate phase heights using only inexpensive volume flow measurements. To this end, a physics-informed neural network (PINN) is first pretrained on synthetic data and physics equations derived from a low-fidelity (approximate) mechanistic model to reduce the need for extensive experimental data. While the mechanistic model is used to generate synthetic training data, only volume balance equations are used in the PINN, since the integration of submodels describing droplet coalescence and sedimentation into the PINN would be computationally prohibitive. The pretrained PINN is then fine-tuned with scarce experimental data to capture the actual dynamics of the separator. We then employ the differentiable PINN as a predictive model in an Extended Kalman Filter inspired state estimation framework, enabling the phase heights to be tracked and updated from flow-rate measurements. We first test the two-stage trained PINN by forward simulation from a known initial state against the mechanistic model and a non-pretrained PINN. We then evaluate phase height estimation performance with the filter, comparing the two-stage trained PINN with a two-stage trained purely data-driven neural network. All model types are trained and evaluated using ensembles to account for model parameter uncertainty. In all evaluations, the two-stage trained PINN yields the most accurate phase-height estimates.

Design of Dynamic Experiments for Black-Box Model Discrimination

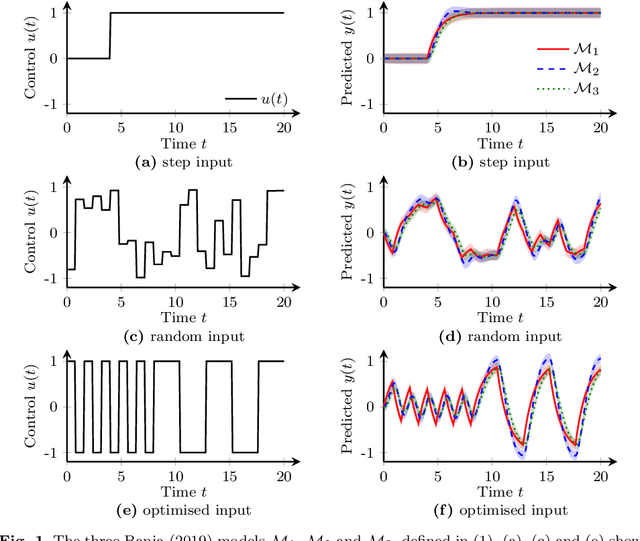
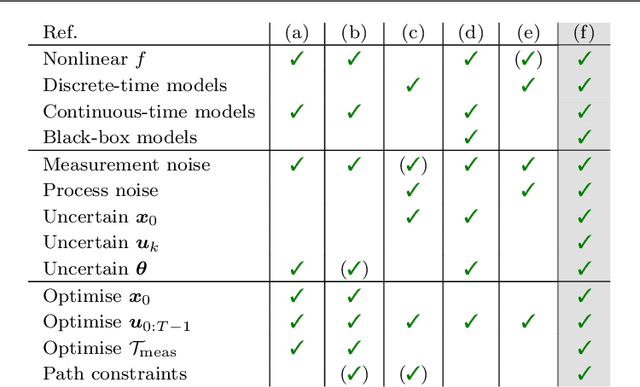
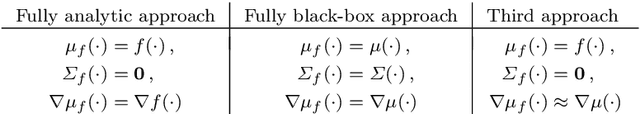
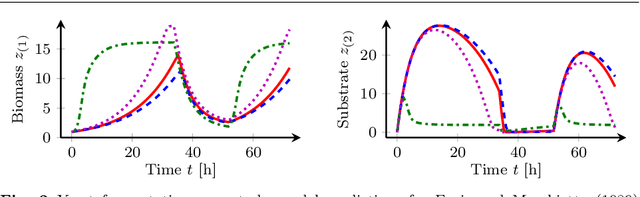
Diverse domains of science and engineering require and use mechanistic mathematical models, e.g. systems of differential algebraic equations. Such models often contain uncertain parameters to be estimated from data. Consider a dynamic model discrimination setting where we wish to chose: (i) what is the best mechanistic, time-varying model and (ii) what are the best model parameter estimates. These tasks are often termed model discrimination/selection/validation/verification. Typically, several rival mechanistic models can explain data, so we incorporate available data and also run new experiments to gather more data. Design of dynamic experiments for model discrimination helps optimally collect data. For rival mechanistic models where we have access to gradient information, we extend existing methods to incorporate a wider range of problem uncertainty and show that our proposed approach is equivalent to historical approaches when limiting the types of considered uncertainty. We also consider rival mechanistic models as dynamic black boxes that we can evaluate, e.g. by running legacy code, but where gradient or other advanced information is unavailable. We replace these black-box models with Gaussian process surrogate models and thereby extend the model discrimination setting to additionally incorporate rival black-box model. We also explore the consequences of using Gaussian process surrogates to approximate gradient-based methods.