A Formalism for Optimal Search with Dynamic Heuristics

While most heuristics studied in heuristic search depend only on the state, some accumulate information during search and thus also depend on the search history. Various existing approaches use such dynamic heuristics in $\mathrm{A}^*$-like algorithms and appeal to classic results for $\mathrm{A}^*$ to show optimality. However, doing so ignores the complexities of searching with a mutable heuristic. In this paper we formalize the idea of dynamic heuristics and use them in a generic algorithm framework. We study a particular instantiation that models $\mathrm{A}^*$ with dynamic heuristics and show general optimality results. Finally we show how existing approaches from classical planning can be viewed as special cases of this instantiation, making it possible to directly apply our optimality results.

Higher-Dimensional Potential Heuristics for Optimal Classical Planning

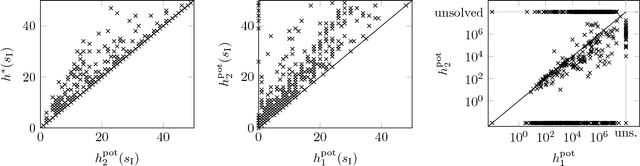
Potential heuristics for state-space search are defined as weighted sums over simple state features. Atomic features consider the value of a single state variable in a factored state representation, while binary features consider joint assignments to two state variables. Previous work showed that the set of all admissible and consistent potential heuristics using atomic features can be characterized by a compact set of linear constraints. We generalize this result to binary features and prove a hardness result for features of higher dimension. Furthermore, we prove a tractability result based on the treewidth of a new graphical structure we call the context-dependency graph. Finally, we study the relationship of potential heuristics to transition cost partitioning. Experimental results show that binary potential heuristics are significantly more informative than the previously considered atomic ones.