Impossibility of Partial Recovery in the Graph Alignment Problem
Paper and Code
Feb 04, 2021
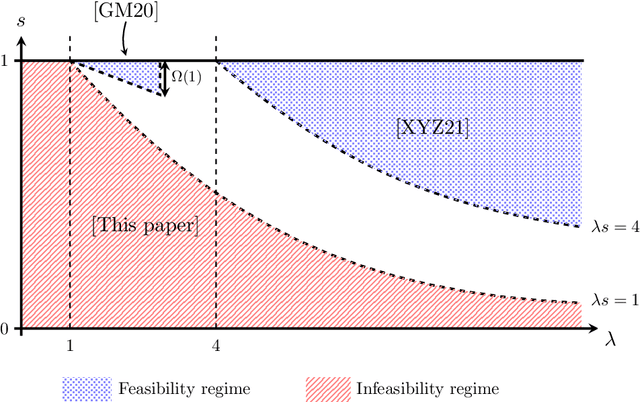
Random graph alignment refers to recovering the underlying vertex correspondence between two random graphs with correlated edges. This can be viewed as an average-case and noisy version of the well-known NP-hard graph isomorphism problem. For the correlated Erd\"os-R\'enyi model, we prove an impossibility result for partial recovery in the sparse regime, with constant average degree and correlation, as well as a general bound on the maximal reachable overlap. Our bound is tight in the noiseless case (the graph isomorphism problem) and we conjecture that it is still tight with noise. Our proof technique relies on a careful application of the probabilistic method to build automorphisms between tree components of a subcritical Erd\"os-R\'enyi graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge