Membership Inference Attacks on Sequence Models

Sequence models, such as Large Language Models (LLMs) and autoregressive image generators, have a tendency to memorize and inadvertently leak sensitive information. While this tendency has critical legal implications, existing tools are insufficient to audit the resulting risks. We hypothesize that those tools' shortcomings are due to mismatched assumptions. Thus, we argue that effectively measuring privacy leakage in sequence models requires leveraging the correlations inherent in sequential generation. To illustrate this, we adapt a state-of-the-art membership inference attack to explicitly model within-sequence correlations, thereby demonstrating how a strong existing attack can be naturally extended to suit the structure of sequence models. Through a case study, we show that our adaptations consistently improve the effectiveness of memorization audits without introducing additional computational costs. Our work hence serves as an important stepping stone toward reliable memorization audits for large sequence models.

DeltaBound Attack: Efficient decision-based attack in low queries regime

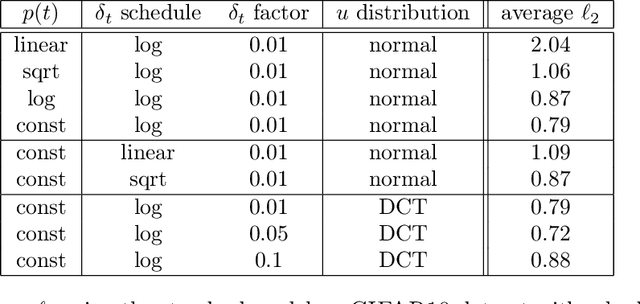
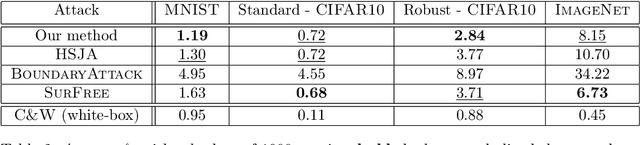
Deep neural networks and other machine learning systems, despite being extremely powerful and able to make predictions with high accuracy, are vulnerable to adversarial attacks. We proposed the DeltaBound attack: a novel, powerful attack in the hard-label setting with $\ell_2$ norm bounded perturbations. In this scenario, the attacker has only access to the top-1 predicted label of the model and can be therefore applied to real-world settings such as remote API. This is a complex problem since the attacker has very little information about the model. Consequently, most of the other techniques present in the literature require a massive amount of queries for attacking a single example. Oppositely, this work mainly focuses on the evaluation of attack's power in the low queries regime $\leq 1000$ queries) with $\ell_2$ norm in the hard-label settings. We find that the DeltaBound attack performs as well and sometimes better than current state-of-the-art attacks while remaining competitive across different kinds of models. Moreover, we evaluate our method against not only deep neural networks, but also non-deep learning models, such as Gradient Boosting Decision Trees and Multinomial Naive Bayes.

Certain and Uncertain Inference with Trivalent Conditionals

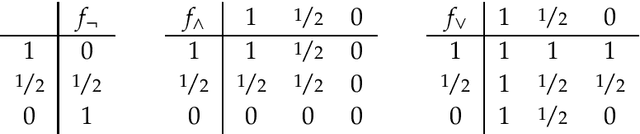
Research on indicative conditionals usually aims either at determining their truth conditions, or at explaining how we should reason with them and when we can assert them. This paper integrates these semantic and epistemological projects by means of articulating trivalent, truth-functional truth conditions for indicative conditionals. Based on this framework, we provide a non-classical account of the probability of conditionals, and two logics of conditional reasoning: (i) a logic C of inference from certain premises that generalizes deductive reasoning; and (ii) a logic U of inference from uncertain premises that generalizes defeasible reasoning. Both logics are highly attractive in their domain. They provide a unified framework for conditional reasoning, generalize existing theories (e.g., Adams's logic of "reasonable inference") and yield an insightful analysis of the controversies about the validity of Modus Ponens, Import-Export, and other principles of conditional logic.