New Statistical and Computational Results for Learning Junta Distributions

We study the problem of learning junta distributions on $\{0, 1\}^n$, where a distribution is a $k$-junta if its probability mass function depends on a subset of at most $k$ variables. We make two main contributions: - We show that learning $k$-junta distributions is \emph{computationally} equivalent to learning $k$-parity functions with noise (LPN), a landmark problem in computational learning theory. - We design an algorithm for learning junta distributions whose statistical complexity is optimal, up to polylogarithmic factors. Computationally, our algorithm matches the complexity of previous (non-sample-optimal) algorithms. Combined, our two contributions imply that our algorithm cannot be significantly improved, statistically or computationally, barring a breakthrough for LPN.

Testing Juntas Optimally with Samples

We prove tight upper and lower bounds of $\Theta\left(\tfrac{1}{\epsilon}\left( \sqrt{2^k \log\binom{n}{k} } + \log\binom{n}{k} \right)\right)$ on the number of samples required for distribution-free $k$-junta testing. This is the first tight bound for testing a natural class of Boolean functions in the distribution-free sample-based model. Our bounds also hold for the feature selection problem, showing that a junta tester must learn the set of relevant variables. For tolerant junta testing, we prove a sample lower bound of $\Omega(2^{(1-o(1)) k} + \log\binom{n}{k})$ showing that, unlike standard testing, there is no large gap between tolerant testing and learning.

Multi-Swap $k$-Means++

The $k$-means++ algorithm of Arthur and Vassilvitskii (SODA 2007) is often the practitioners' choice algorithm for optimizing the popular $k$-means clustering objective and is known to give an $O(\log k)$-approximation in expectation. To obtain higher quality solutions, Lattanzi and Sohler (ICML 2019) proposed augmenting $k$-means++ with $O(k \log \log k)$ local search steps obtained through the $k$-means++ sampling distribution to yield a $c$-approximation to the $k$-means clustering problem, where $c$ is a large absolute constant. Here we generalize and extend their local search algorithm by considering larger and more sophisticated local search neighborhoods hence allowing to swap multiple centers at the same time. Our algorithm achieves a $9 + \varepsilon$ approximation ratio, which is the best possible for local search. Importantly we show that our approach yields substantial practical improvements, we show significant quality improvements over the approach of Lattanzi and Sohler (ICML 2019) on several datasets.

An Optimal Algorithm for Finding Champions in Tournament Graphs

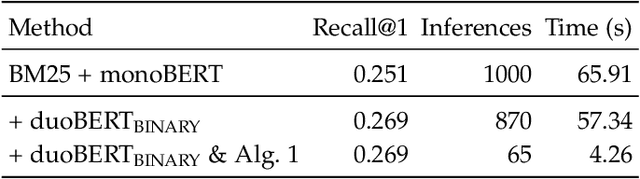
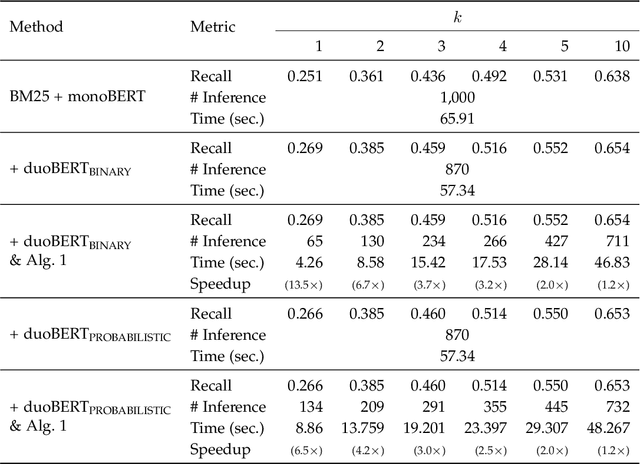
A tournament graph $T = \left(V, E \right)$ is an oriented complete graph, which can be used to model a round-robin tournament between $n$ players. In this paper, we address the problem of finding a champion of the tournament, also known as Copeland winner, which is a player that wins the highest number of matches. Solving this problem has important implications on several Information Retrieval applications, including Web search, conversational IR, machine translation, question answering, recommender systems, etc. Our goal is to solve the problem by minimizing the number of times we probe the adjacency matrix, i.e., the number of matches played. We prove that any deterministic/randomized algorithm finding a champion with constant success probability requires $\Omega(\ell n)$ comparisons, where $\ell$ is the number of matches lost by the champion. We then present an optimal deterministic algorithm matching this lower bound without knowing $\ell$ and we extend our analysis to three strictly related problems. Lastly, we conduct a comprehensive experimental assessment of the proposed algorithms to speed up a state-of-the-art solution for ranking on public data. Results show that our proposals speed up the retrieval of the champion up to $13\times$ in this scenario.