Why the noise model matters: A performance gap in learned regularization

This article addresses the challenge of learning effective regularizers for linear inverse problems. We analyze and compare several types of learned variational regularization against the theoretical benchmark of the optimal affine reconstruction, i.e. the best possible affine linear map for minimizing the mean squared error. It is known that this optimal reconstruction can be achieved using Tikhonov regularization, but this requires precise knowledge of the noise covariance to properly weight the data fidelity term. However, in many practical applications, noise statistics are unknown. We therefore investigate the performance of regularization methods learned without access to this noise information, focusing on Tikhonov, Lavrentiev, and quadratic regularization. Our theoretical analysis and numerical experiments demonstrate that for non-white noise, a performance gap emerges between these methods and the optimal affine reconstruction. Furthermore, we show that these different types of regularization yield distinct results, highlighting that the choice of regularizer structure is critical when the noise model is not explicitly learned. Our findings underscore the significant value of accurately modeling or co-learning noise statistics in data-driven regularization.

Variance Reduction in Deep Learning: More Momentum is All You Need

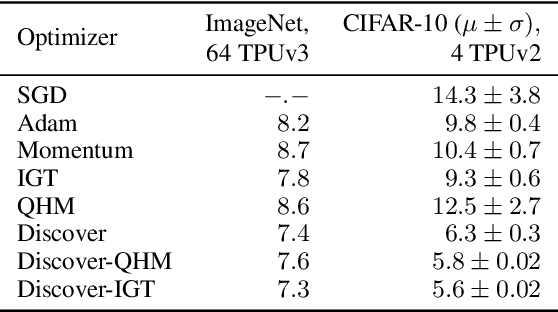
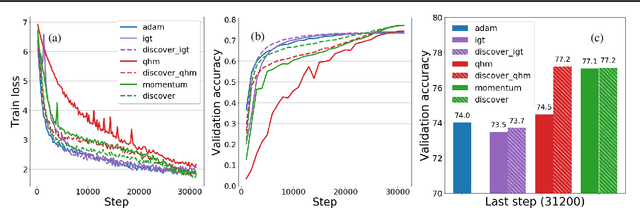
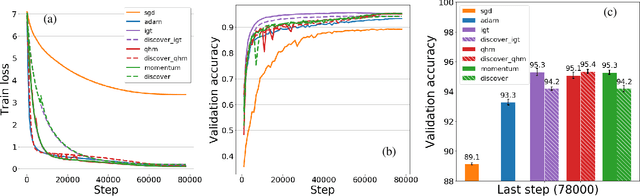
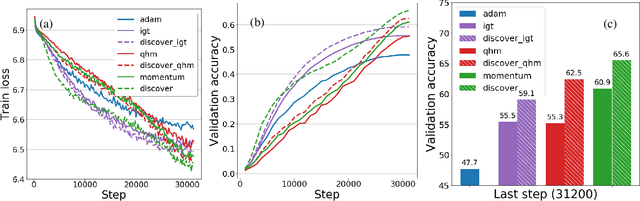
Variance reduction (VR) techniques have contributed significantly to accelerating learning with massive datasets in the smooth and strongly convex setting (Schmidt et al., 2017; Johnson & Zhang, 2013; Roux et al., 2012). However, such techniques have not yet met the same success in the realm of large-scale deep learning due to various factors such as the use of data augmentation or regularization methods like dropout (Defazio & Bottou, 2019). This challenge has recently motivated the design of novel variance reduction techniques tailored explicitly for deep learning (Arnold et al., 2019; Ma & Yarats, 2018). This work is an additional step in this direction. In particular, we exploit the ubiquitous clustering structure of rich datasets used in deep learning to design a family of scalable variance reduced optimization procedures by combining existing optimizers (e.g., SGD+Momentum, Quasi Hyperbolic Momentum, Implicit Gradient Transport) with a multi-momentum strategy (Yuan et al., 2019). Our proposal leads to faster convergence than vanilla methods on standard benchmark datasets (e.g., CIFAR and ImageNet). It is robust to label noise and amenable to distributed optimization. We provide a parallel implementation in JAX.