Constrained and Robust Policy Synthesis with Satisfiability-Modulo-Probabilistic-Model-Checking

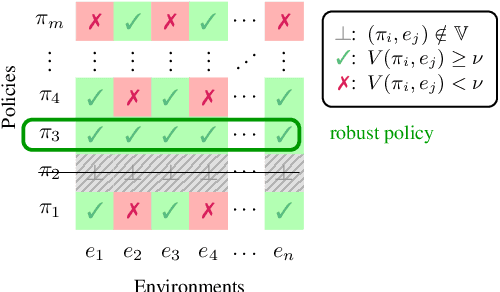
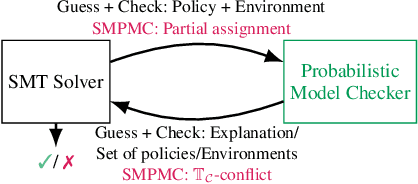
The ability to compute reward-optimal policies for given and known finite Markov decision processes (MDPs) underpins a variety of applications across planning, controller synthesis, and verification. However, we often want policies (1) to be robust, i.e., they perform well on perturbations of the MDP and (2) to satisfy additional structural constraints regarding, e.g., their representation or implementation cost. Computing such robust and constrained policies is indeed computationally more challenging. This paper contributes the first approach to effectively compute robust policies subject to arbitrary structural constraints using a flexible and efficient framework. We achieve flexibility by allowing to express our constraints in a first-order theory over a set of MDPs, while the root for our efficiency lies in the tight integration of satisfiability solvers to handle the combinatorial nature of the problem and probabilistic model checking algorithms to handle the analysis of MDPs. Experiments on a few hundred benchmarks demonstrate the feasibility for constrained and robust policy synthesis and the competitiveness with state-of-the-art methods for various fragments of the problem.

Improving the Noise Estimation of Latent Neural Stochastic Differential Equations

Latent neural stochastic differential equations (SDEs) have recently emerged as a promising approach for learning generative models from stochastic time series data. However, they systematically underestimate the noise level inherent in such data, limiting their ability to capture stochastic dynamics accurately. We investigate this underestimation in detail and propose a straightforward solution: by including an explicit additional noise regularization in the loss function, we are able to learn a model that accurately captures the diffusion component of the data. We demonstrate our results on a conceptual model system that highlights the improved latent neural SDE's capability to model stochastic bistable dynamics.