On Sampling of Multiple Correlated Stochastic Signals

Multiple stochastic signals possess inherent statistical correlations, yet conventional sampling methods that process each channel independently result in data redundancy. To leverage this correlation for efficient sampling, we model correlated channels as a linear combination of a smaller set of uncorrelated, wide-sense stationary latent sources. We establish a theoretical lower bound on the total sampling density for zero mean-square error reconstruction, proving it equals the ratio of the joint spectral bandwidth of latent sources to the number of correlated signal channels. We then develop a constructive multi-band sampling scheme that attains this bound. The proposed method operates via spectral partitioning of the latent sources, followed by spatio-temporal sampling and interpolation. Experiments on synthetic and real datasets confirm that our scheme achieves near-lossless reconstruction precisely at the theoretical sampling density, validating its efficiency.

Bayesian Multi-Scale Optimistic Optimization

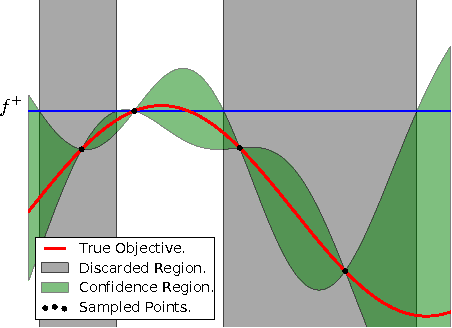
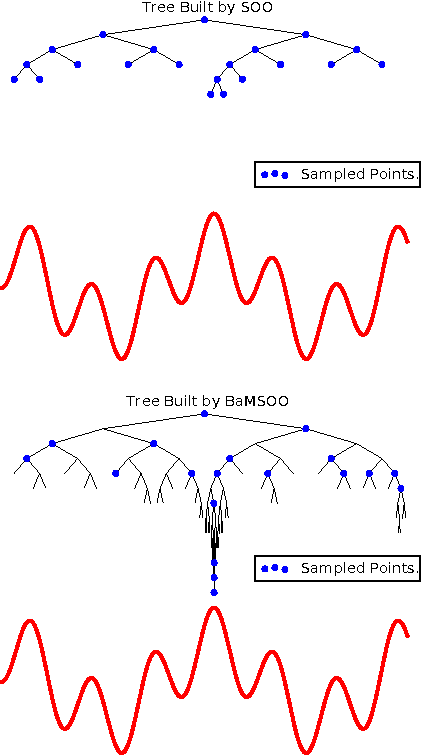
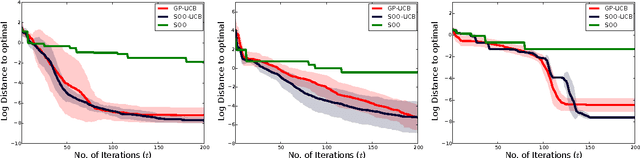
Bayesian optimization is a powerful global optimization technique for expensive black-box functions. One of its shortcomings is that it requires auxiliary optimization of an acquisition function at each iteration. This auxiliary optimization can be costly and very hard to carry out in practice. Moreover, it creates serious theoretical concerns, as most of the convergence results assume that the exact optimum of the acquisition function can be found. In this paper, we introduce a new technique for efficient global optimization that combines Gaussian process confidence bounds and treed simultaneous optimistic optimization to eliminate the need for auxiliary optimization of acquisition functions. The experiments with global optimization benchmarks and a novel application to automatic information extraction demonstrate that the resulting technique is more efficient than the two approaches from which it draws inspiration. Unlike most theoretical analyses of Bayesian optimization with Gaussian processes, our finite-time convergence rate proofs do not require exact optimization of an acquisition function. That is, our approach eliminates the unsatisfactory assumption that a difficult, potentially NP-hard, problem has to be solved in order to obtain vanishing regret rates.