Double-Bounded Optimal Transport for Advanced Clustering and Classification

Optimal transport (OT) is attracting increasing attention in machine learning. It aims to transport a source distribution to a target one at minimal cost. In its vanilla form, the source and target distributions are predetermined, which contracts to the real-world case involving undetermined targets. In this paper, we propose Doubly Bounded Optimal Transport (DB-OT), which assumes that the target distribution is restricted within two boundaries instead of a fixed one, thus giving more freedom for the transport to find solutions. Based on the entropic regularization of DB-OT, three scaling-based algorithms are devised for calculating the optimal solution. We also show that our DB-OT is helpful for barycenter-based clustering, which can avoid the excessive concentration of samples in a single cluster. Then we further develop DB-OT techniques for long-tailed classification which is an emerging and open problem. We first propose a connection between OT and classification, that is, in the classification task, training involves optimizing the Inverse OT to learn the representations, while testing involves optimizing the OT for predictions. With this OT perspective, we first apply DB-OT to improve the loss, and the Balanced Softmax is shown as a special case. Then we apply DB-OT for inference in the testing process. Even with vanilla Softmax trained features, our extensive experimental results show that our method can achieve good results with our improved inference scheme in the testing stage.

IID-GAN: an IID Sampling Perspective for Regularizing Mode Collapse

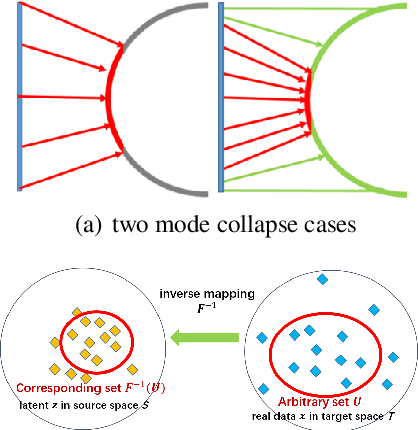
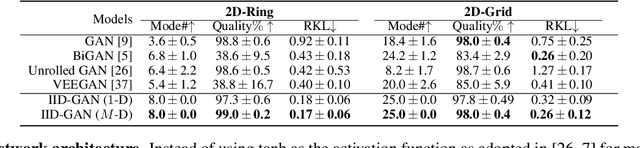
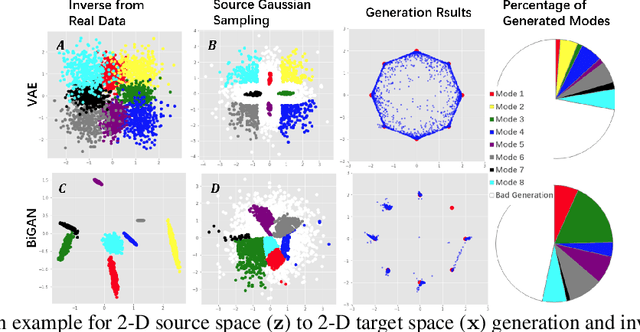
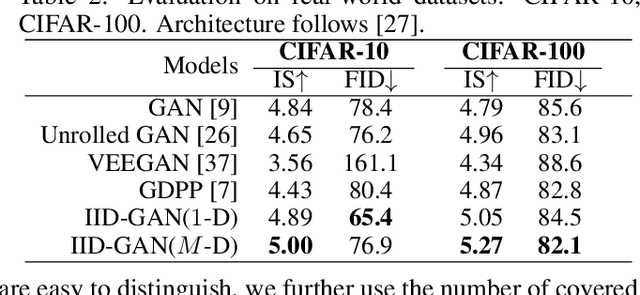
Despite its success, generative adversarial networks (GANs) still suffer from mode collapse, namely the generator can only map latent variables to a partial set of modes of the target distribution. In this paper, we analyze and try to regularize this issue with an independent and identically distributed (IID) sampling perspective and emphasize that holding the IID property for generation in target space (i.e. real data) can naturally avoid mode collapse. This is based on the basic IID assumption for real data in machine learning. However, though the source samples $\mathbf{z}$ obey IID, the target generation $G(\mathbf{z})$ may not necessarily be IID. Based on this observation, we provide a new loss to encourage the closeness between the inverse source from generation, and a standard Gaussian distribution in the latent space, as a way of regularizing the generation to be IID. The logic is that the inverse samples back from target data should also be IID for source distribution. Experiments on both synthetic and real-world data show the superiority and robustness of our model.