Applications of No-Collision Transportation Maps in Manifold Learning

In this work, we investigate applications of no-collision transportation maps introduced in [Nurbekyan et. al., 2020] in manifold learning for image data. Recently, there has been a surge in applying transportation-based distances and features for data representing motion-like or deformation-like phenomena. Indeed, comparing intensities at fixed locations often does not reveal the data structure. No-collision maps and distances developed in [Nurbekyan et. al., 2020] are sensitive to geometric features similar to optimal transportation (OT) maps but much cheaper to compute due to the absence of optimization. In this work, we prove that no-collision distances provide an isometry between translations (respectively dilations) of a single probability measure and the translation (respectively dilation) vectors equipped with a Euclidean distance. Furthermore, we prove that no-collision transportation maps, as well as OT and linearized OT maps, do not in general provide an isometry for rotations. The numerical experiments confirm our theoretical findings and show that no-collision distances achieve similar or better performance on several manifold learning tasks compared to other OT and Euclidean-based methods at a fraction of a computational cost.

Taming Hyperparameter Tuning in Continuous Normalizing Flows Using the JKO Scheme

A normalizing flow (NF) is a mapping that transforms a chosen probability distribution to a normal distribution. Such flows are a common technique used for data generation and density estimation in machine learning and data science. The density estimate obtained with a NF requires a change of variables formula that involves the computation of the Jacobian determinant of the NF transformation. In order to tractably compute this determinant, continuous normalizing flows (CNF) estimate the mapping and its Jacobian determinant using a neural ODE. Optimal transport (OT) theory has been successfully used to assist in finding CNFs by formulating them as OT problems with a soft penalty for enforcing the standard normal distribution as a target measure. A drawback of OT-based CNFs is the addition of a hyperparameter, $\alpha$, that controls the strength of the soft penalty and requires significant tuning. We present JKO-Flow, an algorithm to solve OT-based CNF without the need of tuning $\alpha$. This is achieved by integrating the OT CNF framework into a Wasserstein gradient flow framework, also known as the JKO scheme. Instead of tuning $\alpha$, we repeatedly solve the optimization problem for a fixed $\alpha$ effectively performing a JKO update with a time-step $\alpha$. Hence we obtain a "divide and conquer" algorithm by repeatedly solving simpler problems instead of solving a potentially harder problem with large $\alpha$.

Efficient Natural Gradient Descent Methods for Large-Scale Optimization Problems

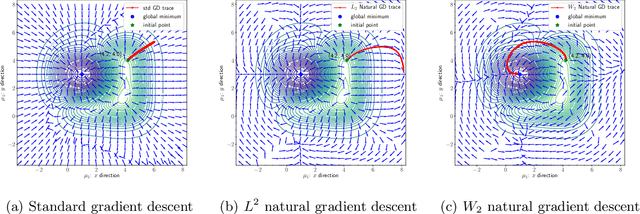
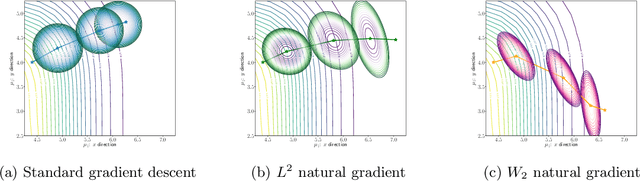
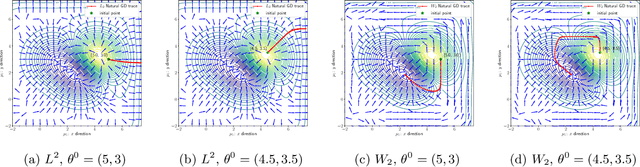
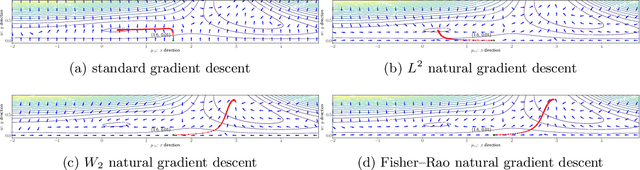
We propose an efficient numerical method for computing natural gradient descent directions with respect to a generic metric in the state space. Our technique relies on representing the natural gradient direction as a solution to a standard least-squares problem. Hence, instead of calculating, storing, or inverting the information matrix directly, we apply efficient methods from numerical linear algebra to solve this least-squares problem. We treat both scenarios where the derivative of the state variable with respect to the parameter is either explicitly known or implicitly given through constraints. We apply the QR decomposition to solve the least-squares problem in the former case and utilize the adjoint-state method to compute the natural gradient descent direction in the latter case. As a result, we can reliably compute several natural gradient descents, including the Wasserstein natural gradient, for a large-scale parameter space with thousands of dimensions, which was believed to be out of reach. Finally, our numerical results shed light on the qualitative differences among the standard gradient descent method and various natural gradient descent methods based on different metric spaces in large-scale nonconvex optimization problems.

APAC-Net: Alternating the Population and Agent Control via Two Neural Networks to Solve High-Dimensional Stochastic Mean Field Games

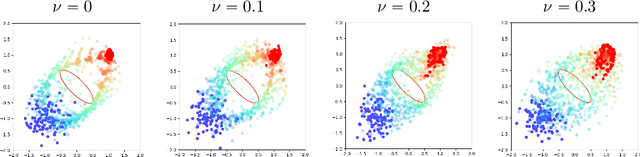
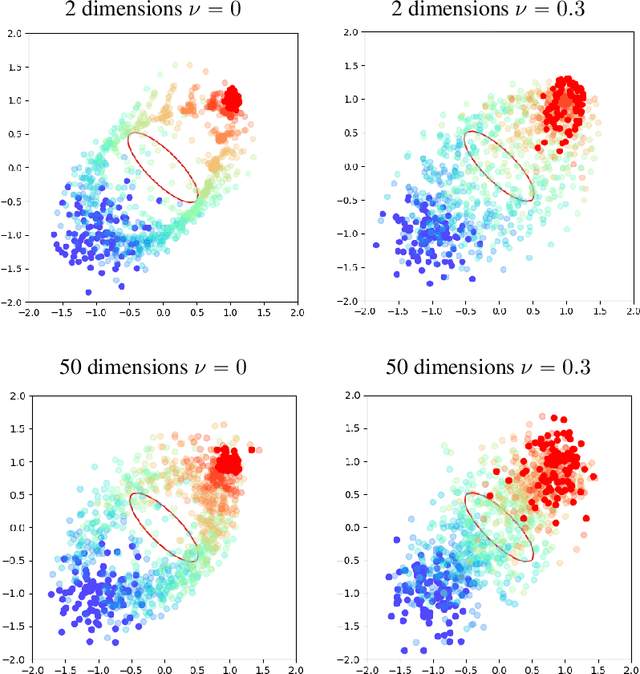
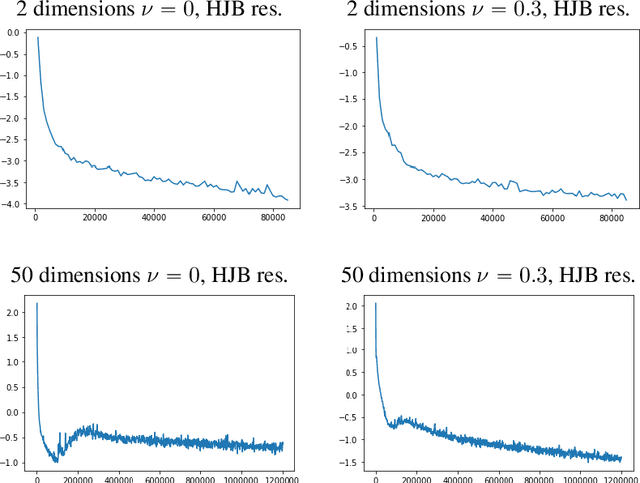
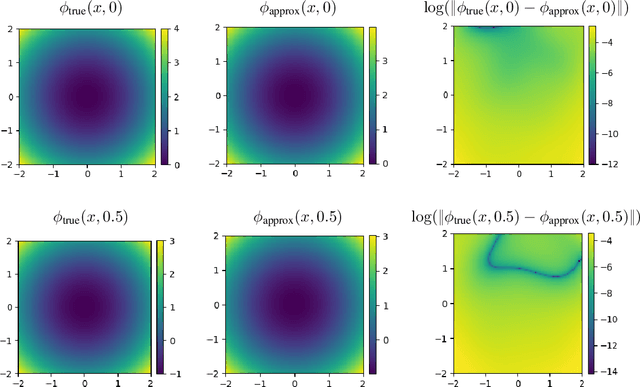
We present APAC-Net, an alternating population and agent control neural network for solving stochastic mean field games (MFGs). Our algorithm is geared toward high-dimensional instances MFGs that are beyond reach with existing solution methods. We achieve this in two steps. First, we take advantage of the underlying variational primal-dual structure that MFGs exhibit and phrase it as a convex-concave saddle point problem. Second, we parameterize the value and density functions by two neural networks, respectively. By phrasing the problem in this manner, solving the MFG can be interpreted as a special case of training a generative adversarial generative network (GAN). We show the potential of our method on up to 50-dimensional MFG problems.

How to train your neural ODE

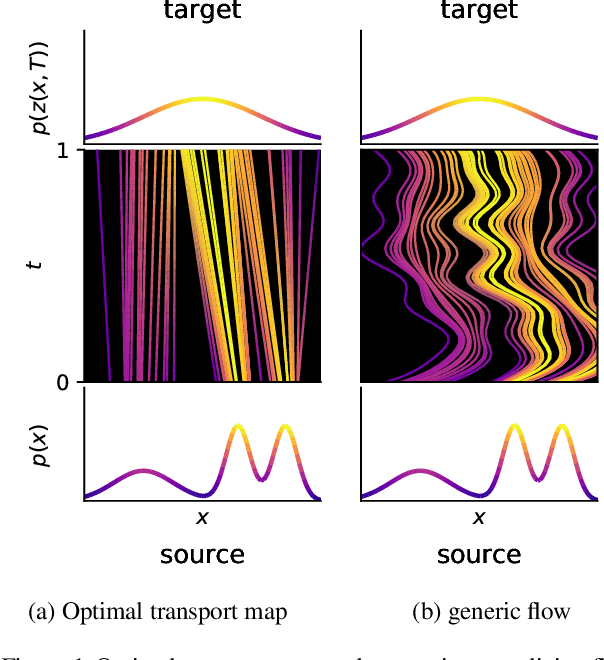
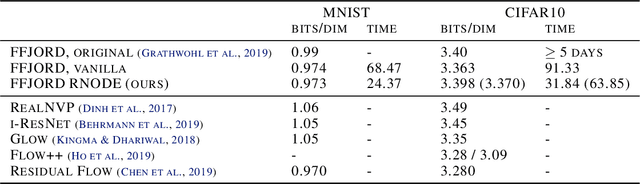
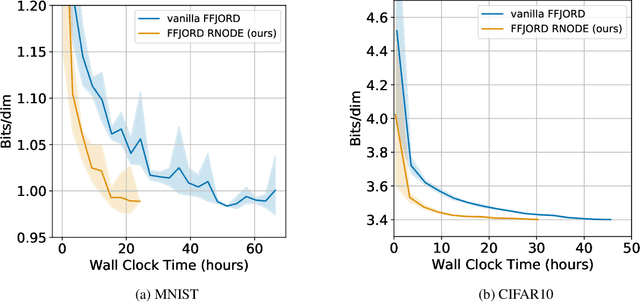
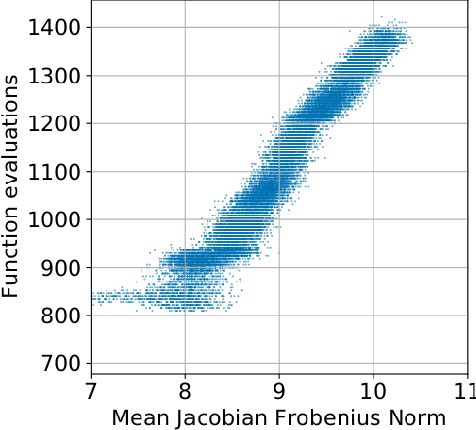
Training neural ODEs on large datasets has not been tractable due to the necessity of allowing the adaptive numerical ODE solver to refine its step size to very small values. In practice this leads to dynamics equivalent to many hundreds or even thousands of layers. In this paper, we overcome this apparent difficulty by introducing a theoretically-grounded combination of both optimal transport and stability regularizations which encourage neural ODEs to prefer simpler dynamics out of all the dynamics that solve a problem well. Simpler dynamics lead to faster convergence and to fewer discretizations of the solver, considerably decreasing wall-clock time without loss in performance. Our approach allows us to train neural ODE based generative models to the same performance as the unregularized dynamics in just over a day on one GPU, whereas unregularized dynamics can take up to 4-6 days of training time on multiple GPUs. This brings neural ODEs significantly closer to practical relevance in large-scale applications.

A Machine Learning Framework for Solving High-Dimensional Mean Field Game and Mean Field Control Problems

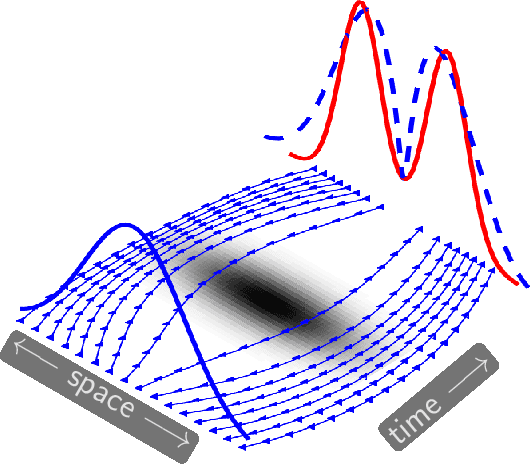
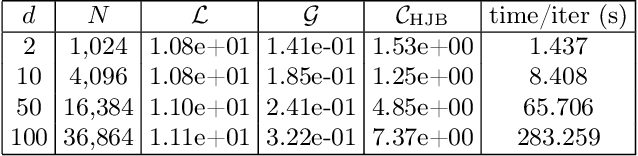
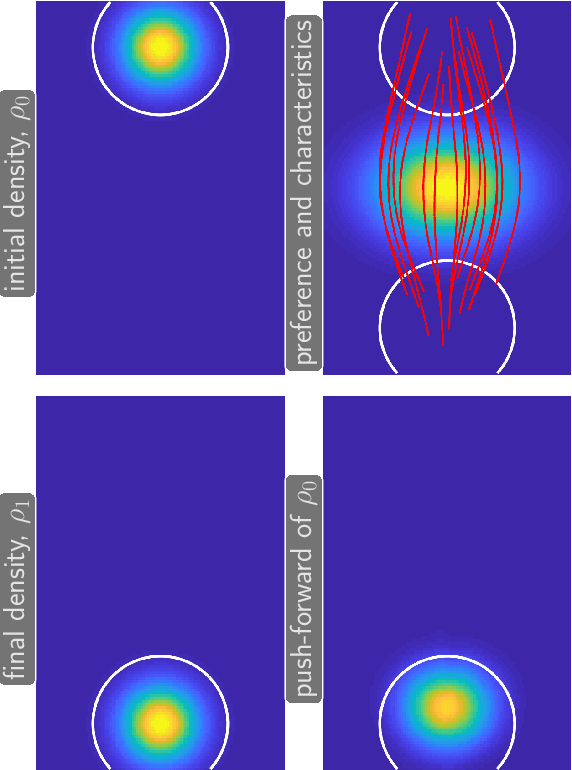
Mean field games (MFG) and mean field control (MFC) are critical classes of multi-agent models for efficient analysis of massive populations of interacting agents. Their areas of application span topics in economics, finance, game theory, industrial engineering, crowd motion, and more. In this paper, we provide a flexible machine learning framework for the numerical solution of potential MFG and MFC models. State-of-the-art numerical methods for solving such problems utilize spatial discretization that leads to a curse-of-dimensionality. We approximately solve high-dimensional problems by combining Lagrangian and Eulerian viewpoints and leveraging recent advances from machine learning. More precisely, we work with a Lagrangian formulation of the problem and enforce the underlying Hamilton-Jacobi-Bellman (HJB) equation that is derived from the Eulerian formulation. Finally, a tailored neural network parameterization of the MFG/MFC solution helps us avoid any spatial discretization. Our numerical results include the approximate solution of 100-dimensional instances of optimal transport and crowd motion problems on a standard work station. These results open the door to much-anticipated applications of MFG and MFC models that were beyond reach with existing numerical methods.