Online Learning with Optimism and Delay

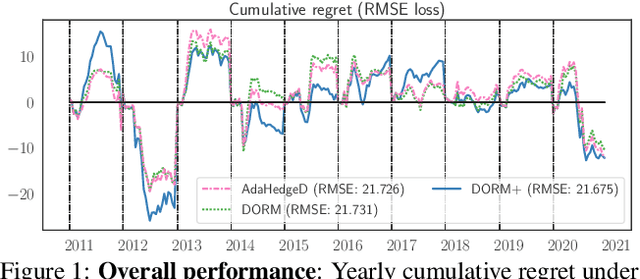
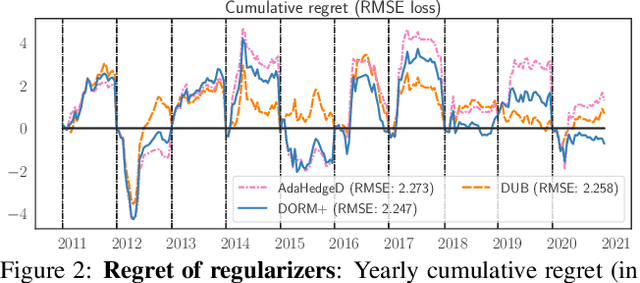
Inspired by the demands of real-time climate and weather forecasting, we develop optimistic online learning algorithms that require no parameter tuning and have optimal regret guarantees under delayed feedback. Our algorithms -- DORM, DORM+, and AdaHedgeD -- arise from a novel reduction of delayed online learning to optimistic online learning that reveals how optimistic hints can mitigate the regret penalty caused by delay. We pair this delay-as-optimism perspective with a new analysis of optimistic learning that exposes its robustness to hinting errors and a new meta-algorithm for learning effective hinting strategies in the presence of delay. We conclude by benchmarking our algorithms on four subseasonal climate forecasting tasks, demonstrating low regret relative to state-of-the-art forecasting models.

Sampling with Mirrored Stein Operators

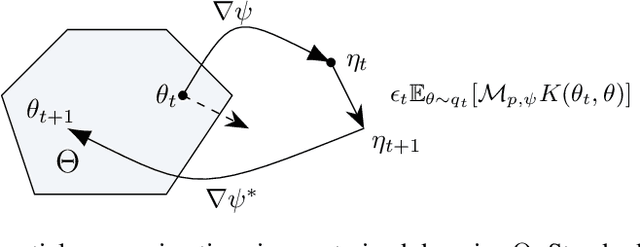
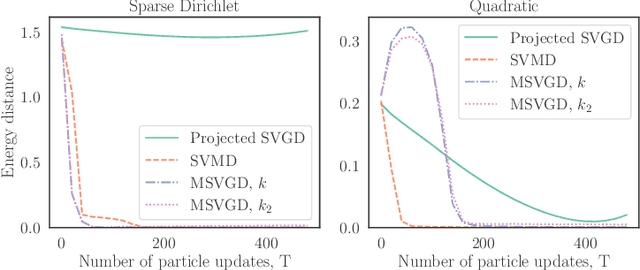
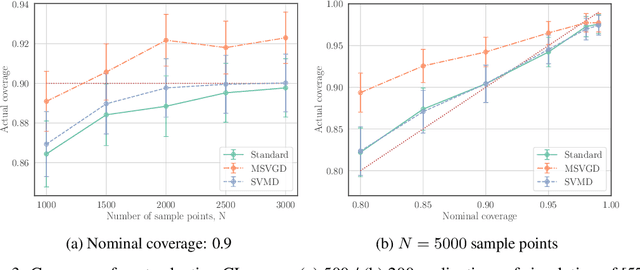
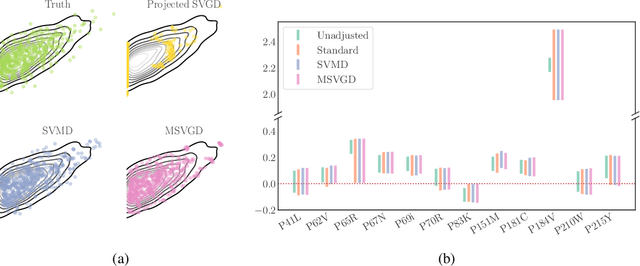
We introduce a new family of particle evolution samplers suitable for constrained domains and non-Euclidean geometries. Stein Variational Mirror Descent and Mirrored Stein Variational Gradient Descent minimize the Kullback-Leibler (KL) divergence to constrained target distributions by evolving particles in a dual space defined by a mirror map. Stein Variational Natural Gradient exploits non-Euclidean geometry to more efficiently minimize the KL divergence to unconstrained targets. We derive these samplers from a new class of mirrored Stein operators and adaptive kernels developed in this work. We demonstrate that these new samplers yield accurate approximations to distributions on the simplex, deliver valid confidence intervals in post-selection inference, and converge more rapidly than prior methods in large-scale unconstrained posterior inference. Finally, we establish the convergence of our new procedures under verifiable conditions on the target distribution.

Kernel Thinning

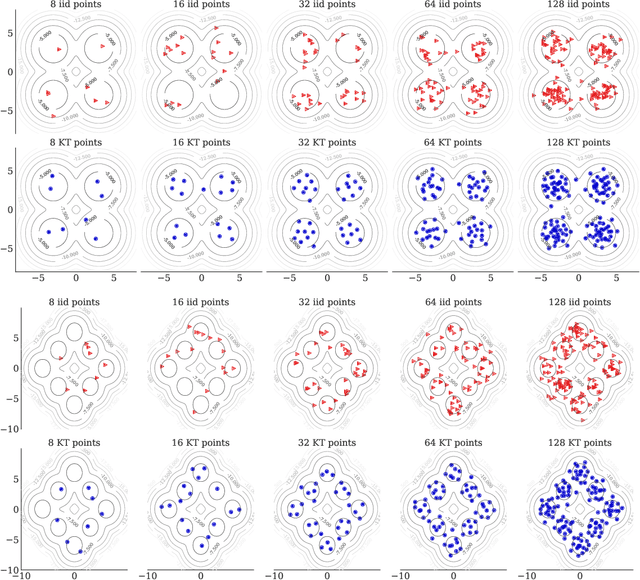
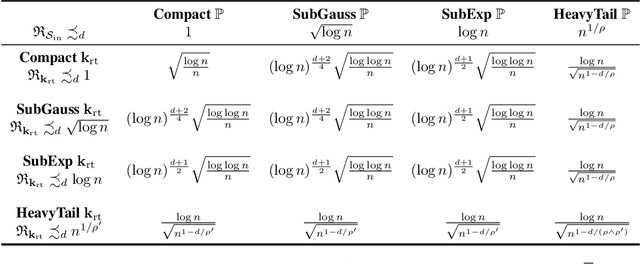
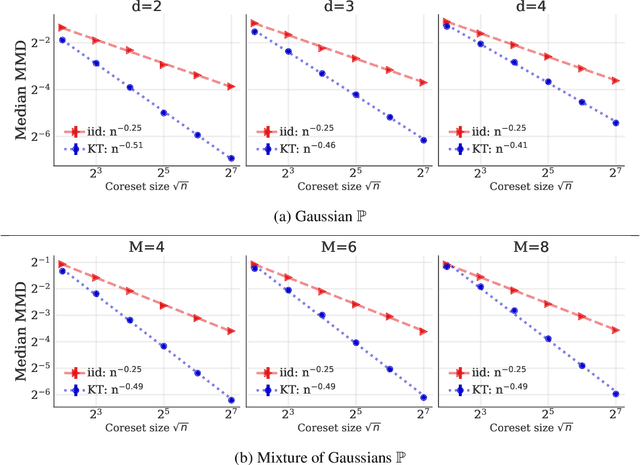
We introduce kernel thinning, a new procedure for compressing a distribution $\mathbb{P}$ more effectively than i.i.d. sampling or standard thinning. Given a suitable reproducing kernel $\mathbf{k}$ and $\mathcal{O}(n^2)$ time, kernel thinning compresses an $n$-point approximation to $\mathbb{P}$ into a $\sqrt{n}$-point approximation with comparable worst-case integration error in the associated reproducing kernel Hilbert space. With high probability, the maximum discrepancy in integration error is $\mathcal{O}_d(n^{-\frac{1}{2}}\sqrt{\log n})$ for compactly supported $\mathbb{P}$ and $\mathcal{O}_d(n^{-\frac{1}{2}} \sqrt{(\log n)^{d+1}\log\log n})$ for sub-exponential $\mathbb{P}$ on $\mathbb{R}^d$. In contrast, an equal-sized i.i.d. sample from $\mathbb{P}$ suffers $\Omega(n^{-\frac14})$ integration error. Our sub-exponential guarantees resemble the classical quasi-Monte Carlo error rates for uniform $\mathbb{P}$ on $[0,1]^d$ but apply to general distributions on $\mathbb{R}^d$ and a wide range of common kernels. We use our results to derive explicit non-asymptotic maximum mean discrepancy bounds for Gaussian, Mat\'ern, and B-spline kernels and present two vignettes illustrating the practical benefits of kernel thinning over i.i.d. sampling and standard Markov chain Monte Carlo thinning.

Initialization and Regularization of Factorized Neural Layers

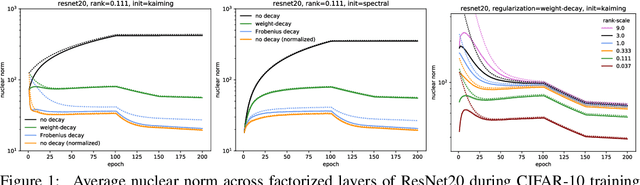
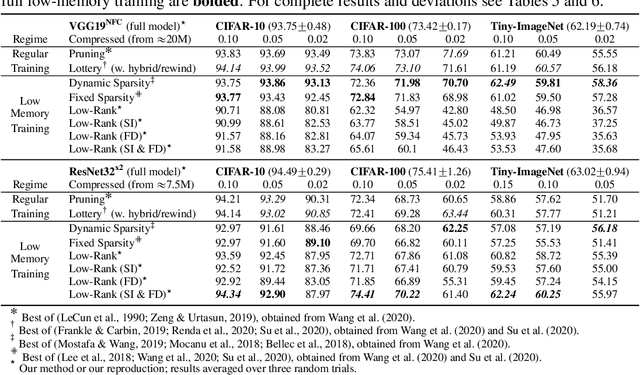
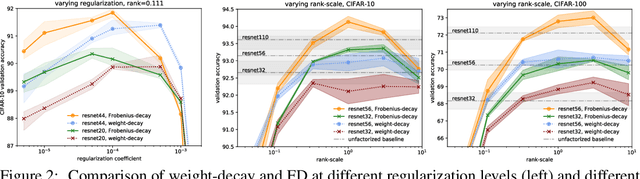
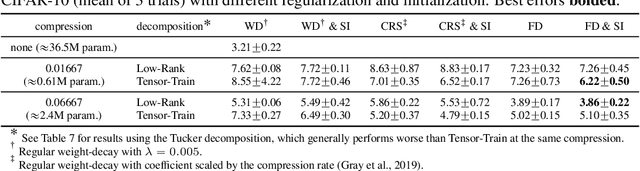
Factorized layers--operations parameterized by products of two or more matrices--occur in a variety of deep learning contexts, including compressed model training, certain types of knowledge distillation, and multi-head self-attention architectures. We study how to initialize and regularize deep nets containing such layers, examining two simple, understudied schemes, spectral initialization and Frobenius decay, for improving their performance. The guiding insight is to design optimization routines for these networks that are as close as possible to that of their well-tuned, non-decomposed counterparts; we back this intuition with an analysis of how the initialization and regularization schemes impact training with gradient descent, drawing on modern attempts to understand the interplay of weight-decay and batch-normalization. Empirically, we highlight the benefits of spectral initialization and Frobenius decay across a variety of settings. In model compression, we show that they enable low-rank methods to significantly outperform both unstructured sparsity and tensor methods on the task of training low-memory residual networks; analogs of the schemes also improve the performance of tensor decomposition techniques. For knowledge distillation, Frobenius decay enables a simple, overcomplete baseline that yields a compact model from over-parameterized training without requiring retraining with or pruning a teacher network. Finally, we show how both schemes applied to multi-head attention lead to improved performance on both translation and unsupervised pre-training.

Knowledge Distillation as Semiparametric Inference

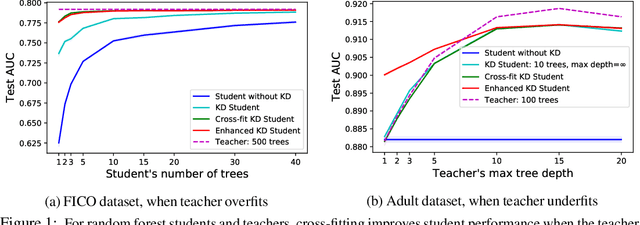
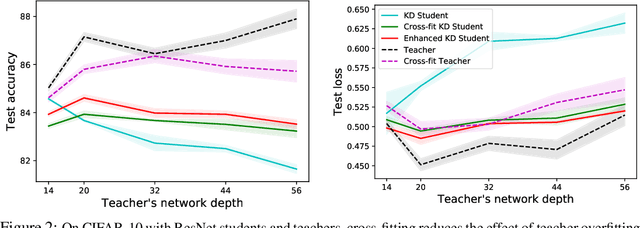
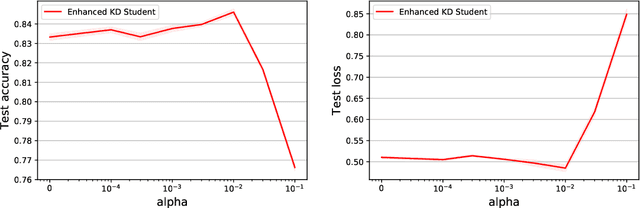
A popular approach to model compression is to train an inexpensive student model to mimic the class probabilities of a highly accurate but cumbersome teacher model. Surprisingly, this two-step knowledge distillation process often leads to higher accuracy than training the student directly on labeled data. To explain and enhance this phenomenon, we cast knowledge distillation as a semiparametric inference problem with the optimal student model as the target, the unknown Bayes class probabilities as nuisance, and the teacher probabilities as a plug-in nuisance estimate. By adapting modern semiparametric tools, we derive new guarantees for the prediction error of standard distillation and develop two enhancements -- cross-fitting and loss correction -- to mitigate the impact of teacher overfitting and underfitting on student performance. We validate our findings empirically on both tabular and image data and observe consistent improvements from our knowledge distillation enhancements.

Model-specific Data Subsampling with Influence Functions

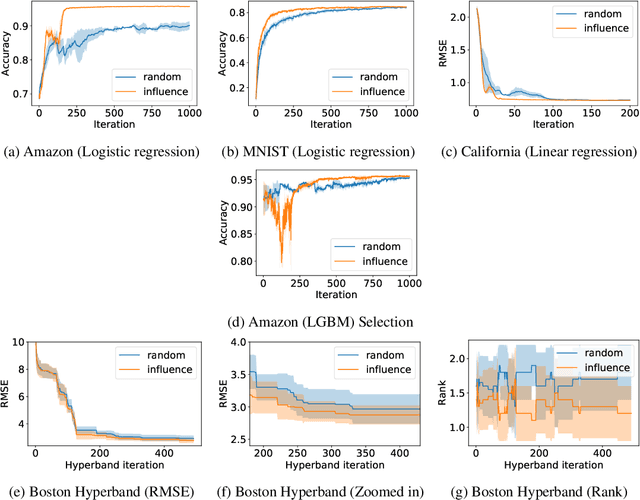
Model selection requires repeatedly evaluating models on a given dataset and measuring their relative performances. In modern applications of machine learning, the models being considered are increasingly more expensive to evaluate and the datasets of interest are increasing in size. As a result, the process of model selection is time-consuming and computationally inefficient. In this work, we develop a model-specific data subsampling strategy that improves over random sampling whenever training points have varying influence. Specifically, we leverage influence functions to guide our selection strategy, proving theoretically, and demonstrating empirically that our approach quickly selects high-quality models.

Independent finite approximations for Bayesian nonparametric inference: construction, error bounds, and practical implications

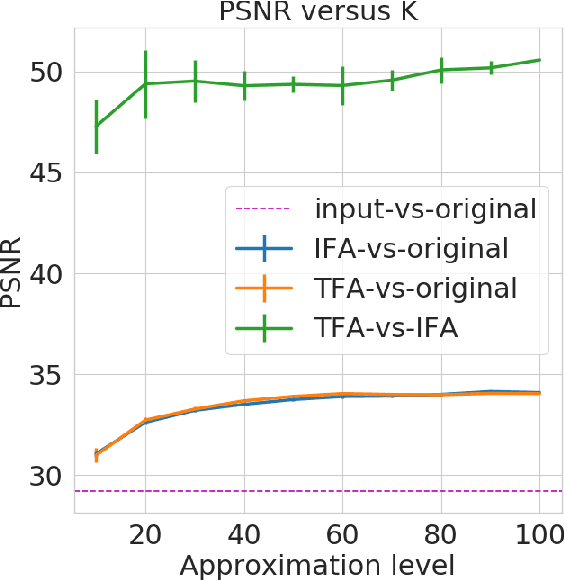
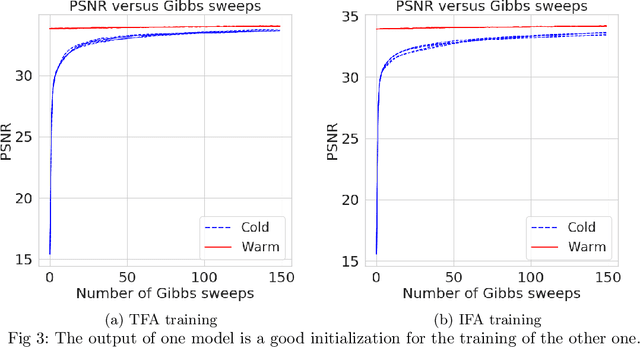
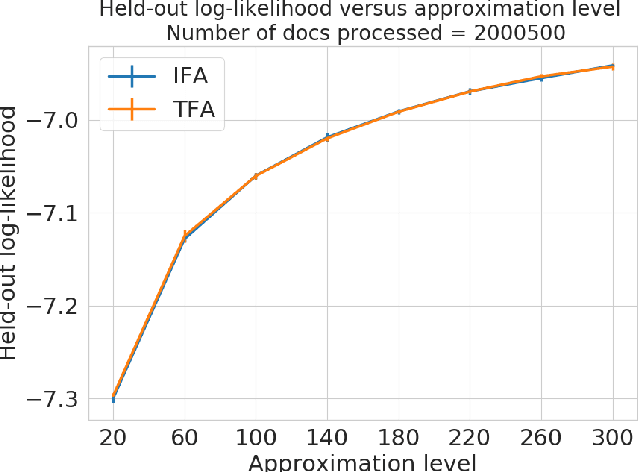
Bayesian nonparametrics based on completely random measures (CRMs) offers a flexible modeling approach when the number of clusters or latent components in a dataset is unknown. However, managing the infinite dimensionality of CRMs often leads to slow computation. Practical inference typically relies on either integrating out the infinite-dimensional parameter or using a finite approximation: a truncated finite approximation (TFA) or an independent finite approximation (IFA). The atom weights of TFAs are constructed sequentially, while the atoms of IFAs are independent, which (1) make them well-suited for parallel and distributed computation and (2) facilitates more convenient inference schemes. While IFAs have been developed in certain special cases in the past, there has not yet been a general template for construction or a systematic comparison to TFAs. We show how to construct IFAs for approximating distributions in a large family of CRMs, encompassing all those typically used in practice. We quantify the approximation error between IFAs and the target nonparametric prior, and prove that, in the worst-case, TFAs provide more component-efficient approximations than IFAs. However, in experiments on image denoising and topic modeling tasks with real data, we find that the error of Bayesian approximation methods overwhelms any finite approximation error, and IFAs perform very similarly to TFAs.

Cross-validation Confidence Intervals for Test Error

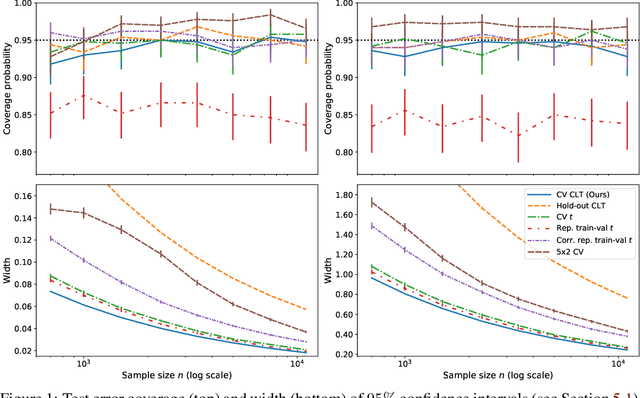
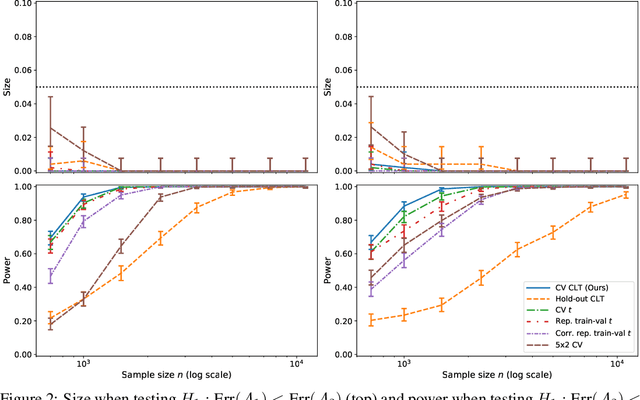
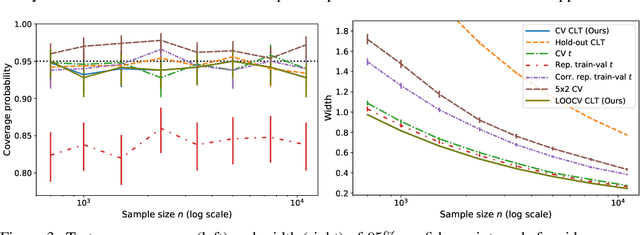
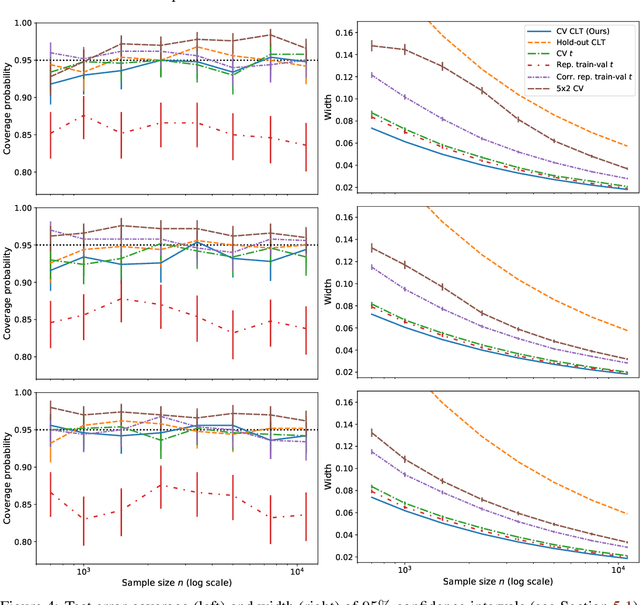
This work develops central limit theorems for cross-validation and consistent estimators of its asymptotic variance under weak stability conditions on the learning algorithm. Together, these results provide practical, asymptotically-exact confidence intervals for $k$-fold test error and valid, powerful hypothesis tests of whether one learning algorithm has smaller $k$-fold test error than another. These results are also the first of their kind for the popular choice of leave-one-out cross-validation. In our real-data experiments with diverse learning algorithms, the resulting intervals and tests outperform the most popular alternative methods from the literature.

Stochastic Stein Discrepancies

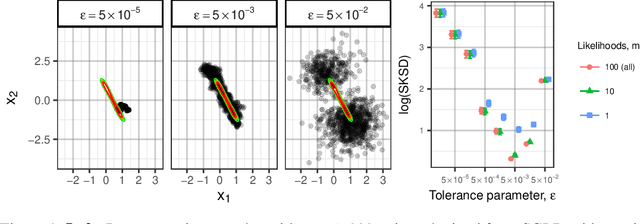
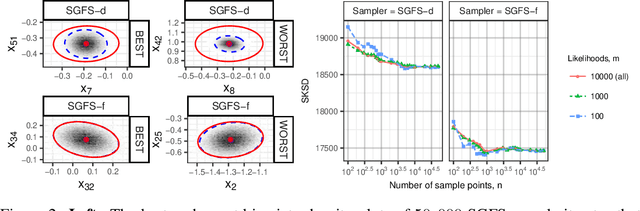
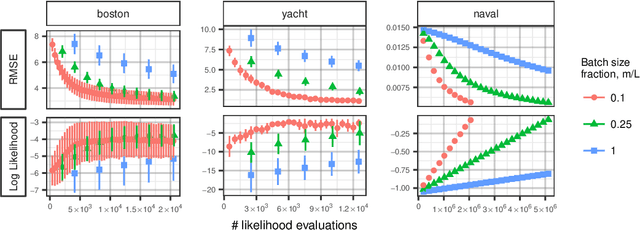
Stein discrepancies (SDs) monitor convergence and non-convergence in approximate inference when exact integration and sampling are intractable. However, the computation of a Stein discrepancy can be prohibitive if the Stein operator - often a sum over likelihood terms or potentials - is expensive to evaluate. To address this deficiency, we show that stochastic Stein discrepancies (SSDs) based on subsampled approximations of the Stein operator inherit the convergence control properties of standard SDs with probability 1. In our experiments with biased Markov chain Monte Carlo (MCMC) hyperparameter tuning, approximate MCMC sampler selection, and stochastic Stein variational gradient descent, SSDs deliver comparable inferences to standard SDs with orders of magnitude fewer likelihood evaluations.

Metrizing Weak Convergence with Maximum Mean Discrepancies

Theorem 12 of Simon-Gabriel & Sch\"olkopf (JMLR, 2018) seemed to close a 40-year-old quest to characterize maximum mean discrepancies (MMD) that metrize the weak convergence of probability measures. We prove, however, that the theorem is incorrect and provide a correction. We show that, on a locally compact, non-compact, Hausdorff space, the MMD of a bounded continuous Borel measurable kernel k, whose RKHS-functions vanish at infinity, metrizes the weak convergence of probability measures if and only if k is continuous and integrally strictly positive definite (ISPD) over all signed, finite, regular Borel measures. We also show that, contrary to the claim of the aforementioned Theorem 12, there exist both bounded continuous ISPD kernels that do not metrize weak convergence and bounded continuous non-ISPD kernels that do metrize it.