Sampling-Based Methods for Factored Task and Motion Planning

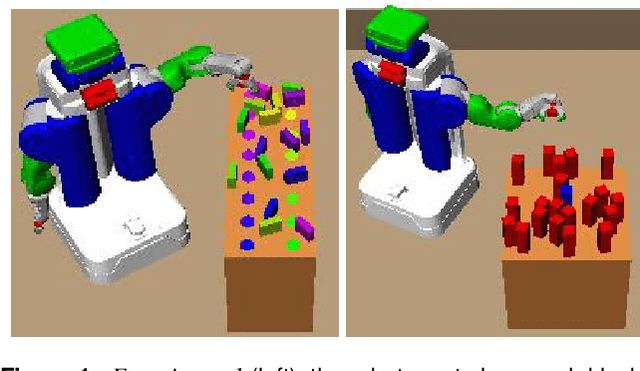
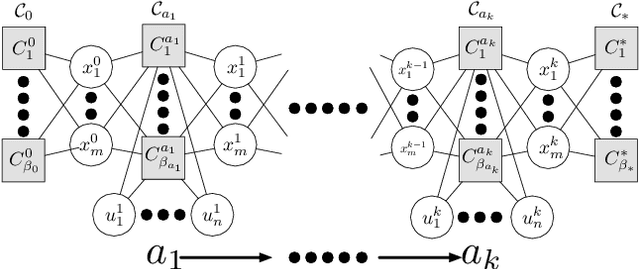
This paper presents a general-purpose formulation of a large class of discrete-time planning problems, with hybrid state and control-spaces, as factored transition systems. Factoring allows state transitions to be described as the intersection of several constraints each affecting a subset of the state and control variables. Robotic manipulation problems with many movable objects involve constraints that only affect several variables at a time and therefore exhibit large amounts of factoring. We develop a theoretical framework for solving factored transition systems with sampling-based algorithms. The framework characterizes conditions on the submanifold in which solutions lie, leading to a characterization of robust feasibility that incorporates dimensionality-reducing constraints. It then connects those conditions to corresponding conditional samplers that can be composed to produce values on this submanifold. We present two domain-independent, probabilistically complete planning algorithms that take, as input, a set of conditional samplers. We demonstrate the empirical efficiency of these algorithms on a set of challenging task and motion planning problems involving picking, placing, and pushing.

Look before you sweep: Visibility-aware motion planning

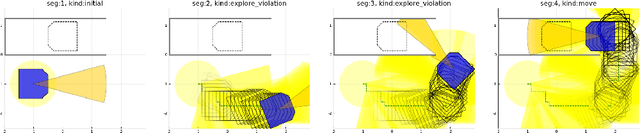
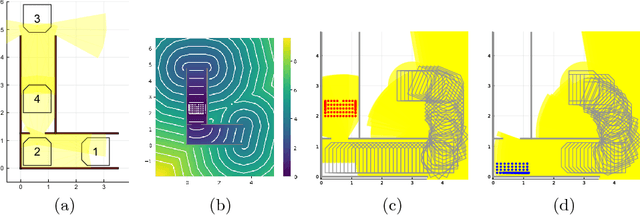
This paper addresses the problem of planning for a robot with a directional obstacle-detection sensor that must move through a cluttered environment. The planning objective is to remain safe by finding a path for the complete robot, including sensor, that guarantees that the robot will not move into any part of the workspace before it has been seen by the sensor. Although a great deal of work has addressed a version of this problem in which the "field of view" of the sensor is a sphere around the robot, there is very little work addressing robots with a narrow or occluded field of view. We give a formal definition of the problem, several solution methods with different computational trade-offs, and experimental results in illustrative domains.

Elimination of All Bad Local Minima in Deep Learning

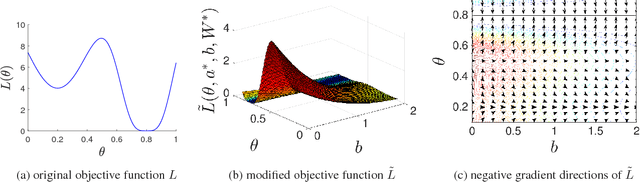
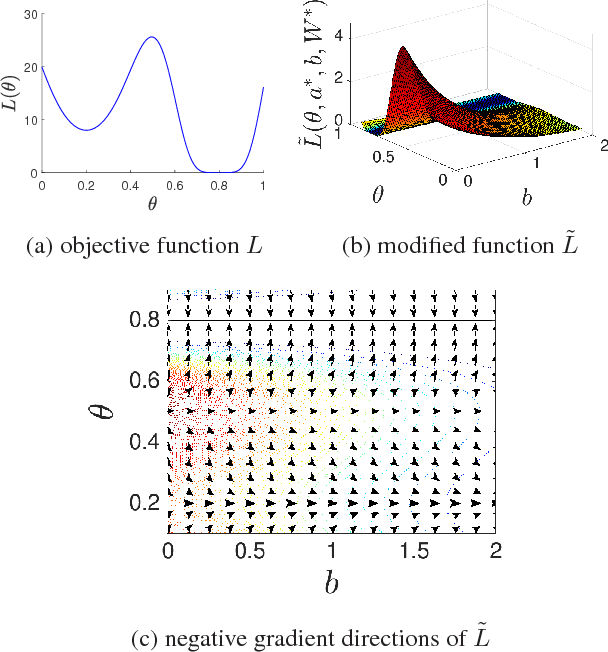
In this paper, we theoretically prove that we can eliminate all suboptimal local minima by adding one neuron per output unit to any deep neural network, for multi-class classification, binary classification, and regression with an arbitrary loss function. At every local minimum of any deep neural network with added neurons, the set of parameters of the original neural network (without added neurons) is guaranteed to be a global minimum of the original neural network. The effects of the added neurons are proven to automatically vanish at every local minimum. Unlike many related results in the literature, our theoretical results are directly applicable to common deep learning tasks because the results only rely on the assumptions that automatically hold in the common tasks. Moreover, we discuss several limitations in eliminating the suboptimal local minima in this manner by providing additional theoretical results and several examples.

Regret bounds for meta Bayesian optimization with an unknown Gaussian process prior

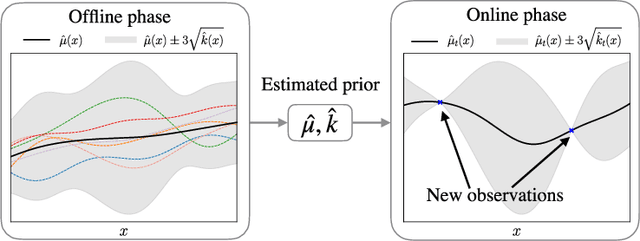
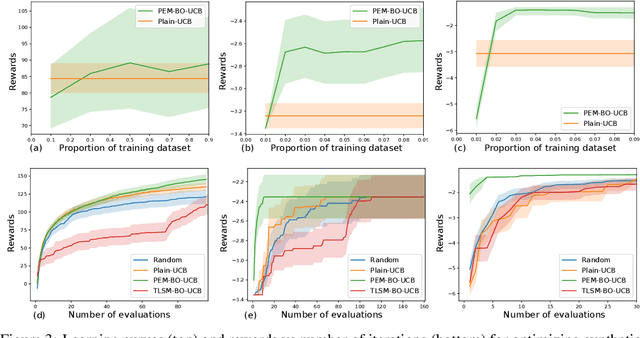
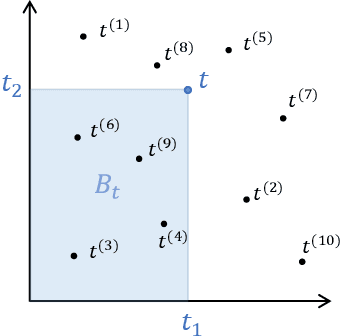
Bayesian optimization usually assumes that a Bayesian prior is given. However, the strong theoretical guarantees in Bayesian optimization are often regrettably compromised in practice because of unknown parameters in the prior. In this paper, we adopt a variant of empirical Bayes and show that, by estimating the Gaussian process prior from offline data sampled from the same prior and constructing unbiased estimators of the posterior, variants of both GP-UCB and probability of improvement achieve a near-zero regret bound, which decreases to a constant proportional to the observational noise as the number of offline data and the number of online evaluations increase. Empirically, we have verified our approach on challenging simulated robotic problems featuring task and motion planning.

Effect of Depth and Width on Local Minima in Deep Learning

In this paper, we analyze the effects of depth and width on the quality of local minima, without strong over-parameterization and simplification assumptions in the literature. Without any simplification assumption, for deep nonlinear neural networks with the squared loss, we theoretically show that the quality of local minima tends to improve towards the global minimum value as depth and width increase. Furthermore, with a locally-induced structure on deep nonlinear neural networks, the values of local minima of neural networks are theoretically proven to be no worse than the globally optimal values of corresponding classical machine learning models. We empirically support our theoretical observation with a synthetic dataset as well as MNIST, CIFAR-10 and SVHN datasets. When compared to previous studies with strong over-parameterization assumptions, the results in this paper do not require over-parameterization, and instead show the gradual effects of over-parameterization as consequences of general results.

Learning sparse relational transition models

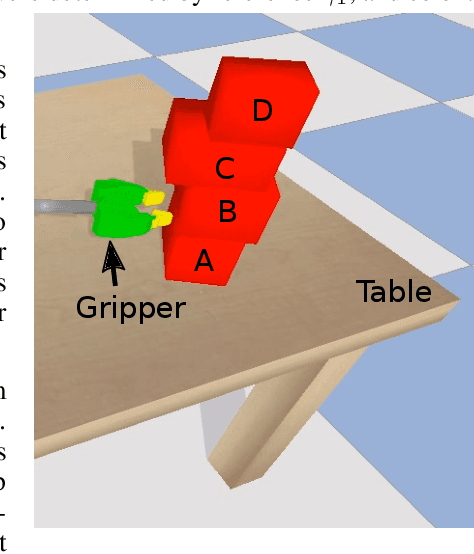
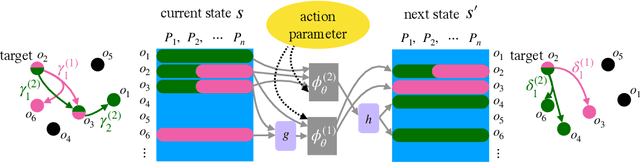
We present a representation for describing transition models in complex uncertain domains using relational rules. For any action, a rule selects a set of relevant objects and computes a distribution over properties of just those objects in the resulting state given their properties in the previous state. An iterative greedy algorithm is used to construct a set of deictic references that determine which objects are relevant in any given state. Feed-forward neural networks are used to learn the transition distribution on the relevant objects' properties. This strategy is demonstrated to be both more versatile and more sample efficient than learning a monolithic transition model in a simulated domain in which a robot pushes stacks of objects on a cluttered table.

Towards Understanding Generalization via Analytical Learning Theory

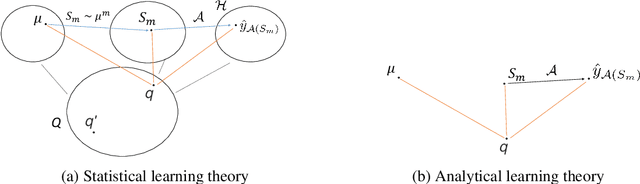
This paper introduces a novel measure-theoretic theory for machine learning that does not require statistical assumptions. Based on this theory, a new regularization method in deep learning is derived and shown to outperform previous methods in CIFAR-10, CIFAR-100, and SVHN. Moreover, the proposed theory provides a theoretical basis for a family of practically successful regularization methods in deep learning. We discuss several consequences of our results on one-shot learning, representation learning, deep learning, and curriculum learning. Unlike statistical learning theory, the proposed learning theory analyzes each problem instance individually via measure theory, rather than a set of problem instances via statistics. As a result, it provides different types of results and insights when compared to statistical learning theory.

Learning What Information to Give in Partially Observed Domains

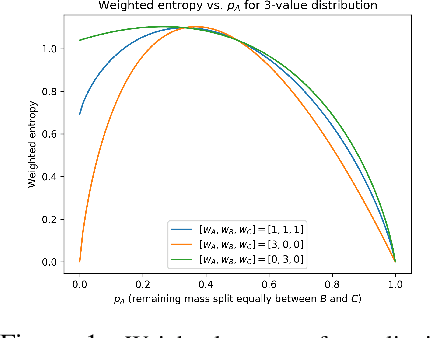
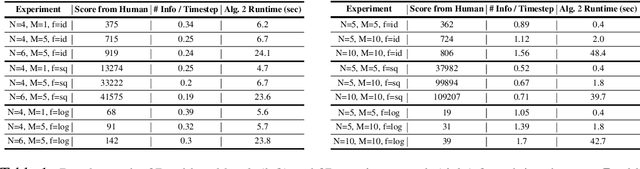
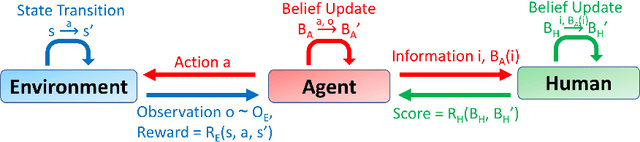
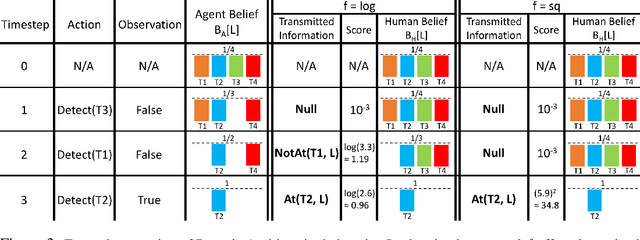
In many robotic applications, an autonomous agent must act within and explore a partially observed environment that is unobserved by its human teammate. We consider such a setting in which the agent can, while acting, transmit declarative information to the human that helps them understand aspects of this unseen environment. In this work, we address the algorithmic question of how the agent should plan out what actions to take and what information to transmit. Naturally, one would expect the human to have preferences, which we model information-theoretically by scoring transmitted information based on the change it induces in weighted entropy of the human's belief state. We formulate this setting as a belief MDP and give a tractable algorithm for solving it approximately. Then, we give an algorithm that allows the agent to learn the human's preferences online, through exploration. We validate our approach experimentally in simulated discrete and continuous partially observed search-and-recover domains. Visit http://tinyurl.com/chitnis-corl-18 for a supplementary video.

Active model learning and diverse action sampling for task and motion planning

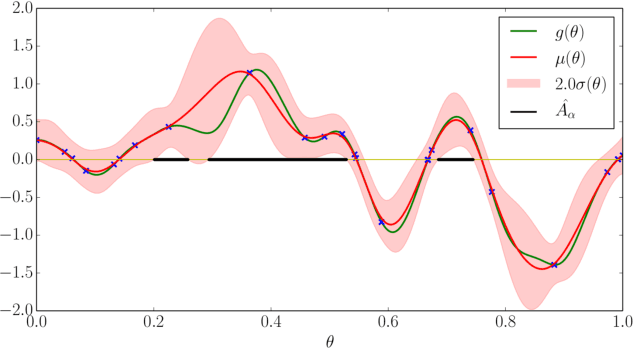
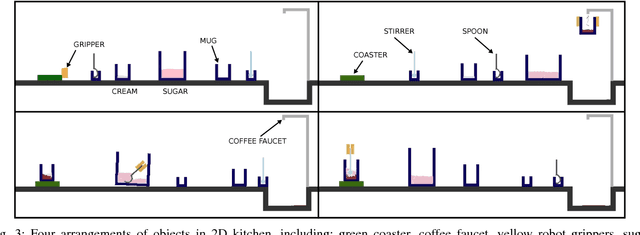
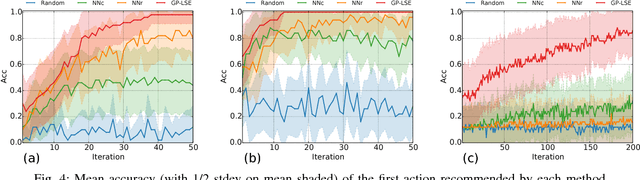
The objective of this work is to augment the basic abilities of a robot by learning to use new sensorimotor primitives to enable the solution of complex long-horizon problems. Solving long-horizon problems in complex domains requires flexible generative planning that can combine primitive abilities in novel combinations to solve problems as they arise in the world. In order to plan to combine primitive actions, we must have models of the preconditions and effects of those actions: under what circumstances will executing this primitive achieve some particular effect in the world? We use, and develop novel improvements on, state-of-the-art methods for active learning and sampling. We use Gaussian process methods for learning the conditions of operator effectiveness from small numbers of expensive training examples collected by experimentation on a robot. We develop adaptive sampling methods for generating diverse elements of continuous sets (such as robot configurations and object poses) during planning for solving a new task, so that planning is as efficient as possible. We demonstrate these methods in an integrated system, combining newly learned models with an efficient continuous-space robot task and motion planner to learn to solve long horizon problems more efficiently than was previously possible.

Integrating Human-Provided Information Into Belief State Representation Using Dynamic Factorization

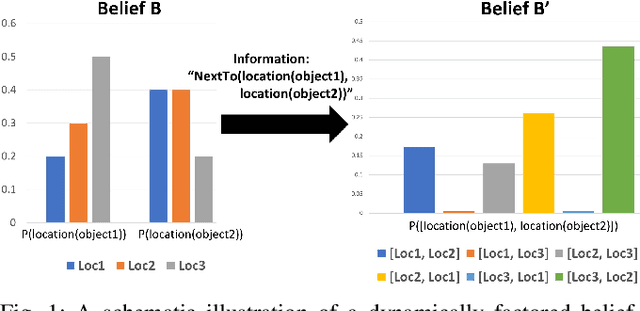
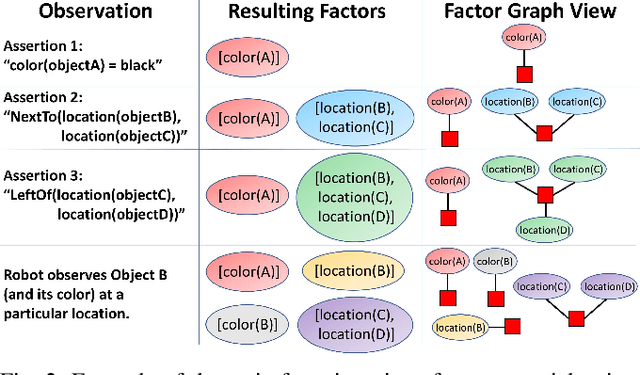
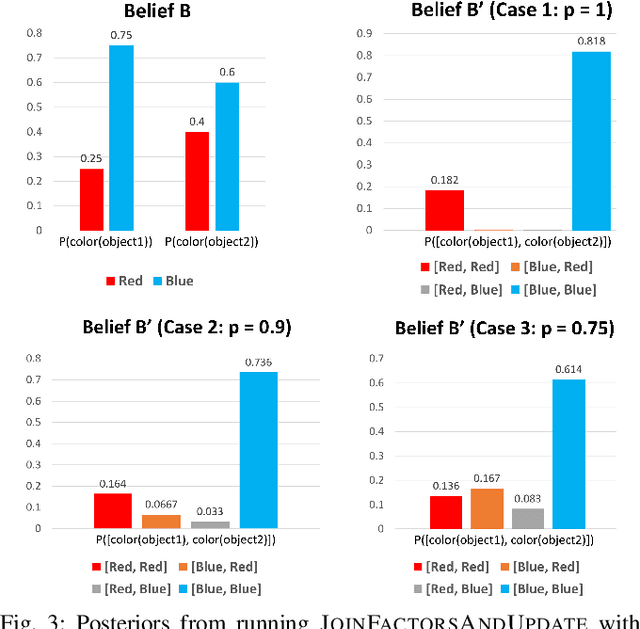
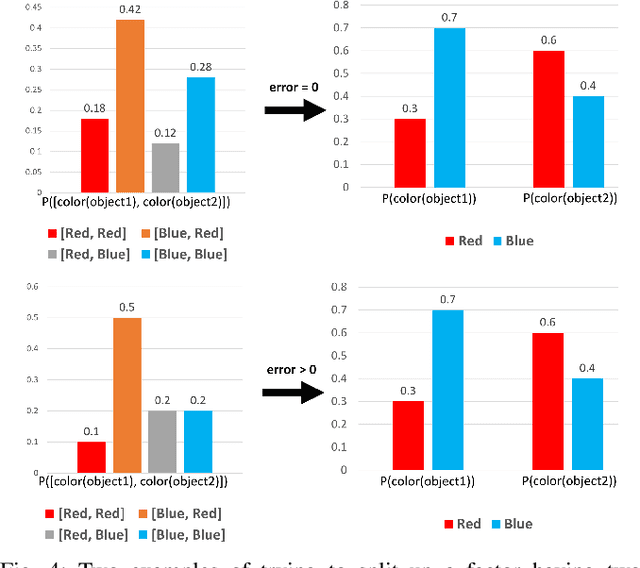
In partially observed environments, it can be useful for a human to provide the robot with declarative information that represents probabilistic relational constraints on properties of objects in the world, augmenting the robot's sensory observations. For instance, a robot tasked with a search-and-rescue mission may be informed by the human that two victims are probably in the same room. An important question arises: how should we represent the robot's internal knowledge so that this information is correctly processed and combined with raw sensory information? In this paper, we provide an efficient belief state representation that dynamically selects an appropriate factoring, combining aspects of the belief when they are correlated through information and separating them when they are not. This strategy works in open domains, in which the set of possible objects is not known in advance, and provides significant improvements in inference time over a static factoring, leading to more efficient planning for complex partially observed tasks. We validate our approach experimentally in two open-domain planning problems: a 2D discrete gridworld task and a 3D continuous cooking task. A supplementary video can be found at http://tinyurl.com/chitnis-iros-18.