On the symmetries in the dynamics of wide two-layer neural networks

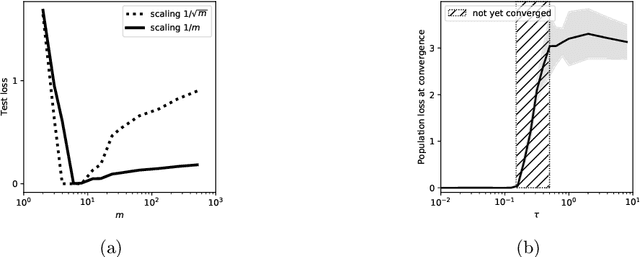
We consider the idealized setting of gradient flow on the population risk for infinitely wide two-layer ReLU neural networks (without bias), and study the effect of symmetries on the learned parameters and predictors. We first describe a general class of symmetries which, when satisfied by the target function $f^*$ and the input distribution, are preserved by the dynamics. We then study more specific cases. When $f^*$ is odd, we show that the dynamics of the predictor reduces to that of a (non-linearly parameterized) linear predictor, and its exponential convergence can be guaranteed. When $f^*$ has a low-dimensional structure, we prove that the gradient flow PDE reduces to a lower-dimensional PDE. Furthermore, we present informal and numerical arguments that suggest that the input neurons align with the lower-dimensional structure of the problem.

Faster Wasserstein Distance Estimation with the Sinkhorn Divergence

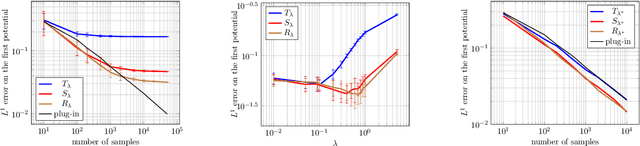
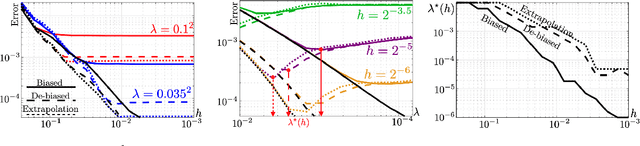
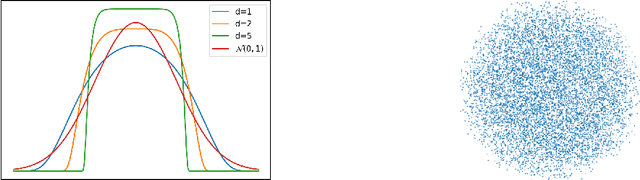
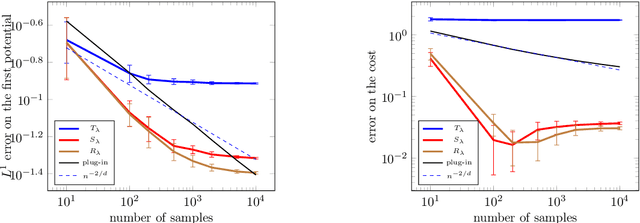
The squared Wasserstein distance is a natural quantity to compare probability distributions in a non-parametric setting. This quantity is usually estimated with the plug-in estimator, defined via a discrete optimal transport problem. It can be solved to $\epsilon$-accuracy by adding an entropic regularization of order $\epsilon$ and using for instance Sinkhorn's algorithm. In this work, we propose instead to estimate it with the Sinkhorn divergence, which is also built on entropic regularization but includes debiasing terms. We show that, for smooth densities, this estimator has a comparable sample complexity but allows higher regularization levels, of order $\epsilon^{1/2}$ , which leads to improved computational complexity bounds and a strong speedup in practice. Our theoretical analysis covers the case of both randomly sampled densities and deterministic discretizations on uniform grids. We also propose and analyze an estimator based on Richardson extrapolation of the Sinkhorn divergence which enjoys improved statistical and computational efficiency guarantees, under a condition on the regularity of the approximation error, which is in particular satisfied for Gaussian densities. We finally demonstrate the efficiency of the proposed estimators with numerical experiments.

Implicit Bias of Gradient Descent for Wide Two-layer Neural Networks Trained with the Logistic Loss

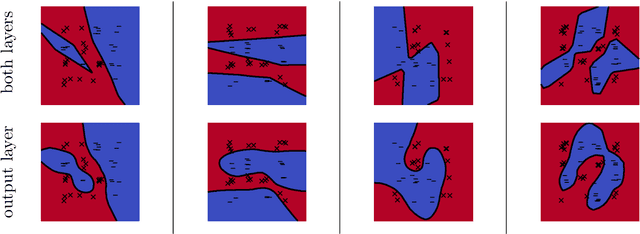
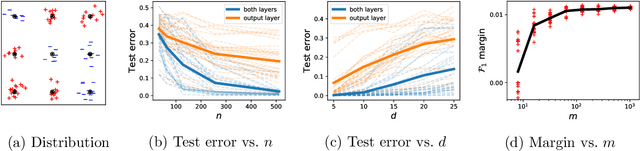
Neural networks trained to minimize the logistic (a.k.a. cross-entropy) loss with gradient-based methods are observed to perform well in many supervised classification tasks. Towards understanding this phenomenon, we analyze the training and generalization behavior of infinitely wide two-layer neural networks with homogeneous activations. We show that the limits of the gradient flow on exponentially tailed losses can be fully characterized as a max-margin classifier in a certain non-Hilbertian space of functions. In presence of hidden low-dimensional structures, the resulting margin is independent of the ambiant dimension, which leads to strong generalization bounds. In contrast, training only the output layer implicitly solves a kernel support vector machine, which a priori does not enjoy such an adaptivity. Our analysis of training is non-quantitative in terms of running time but we prove computational guarantees in simplified settings by showing equivalences with online mirror descent. Finally, numerical experiments suggest that our analysis describes well the practical behavior of two-layer neural networks with ReLU activation and confirm the statistical benefits of this implicit bias.

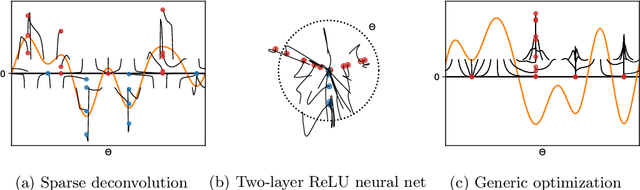
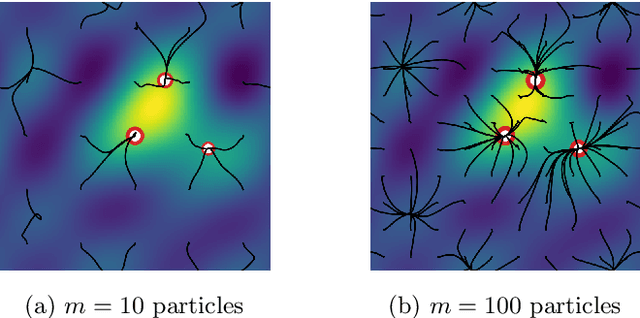
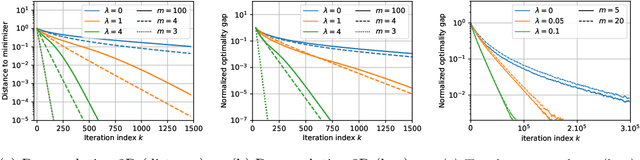
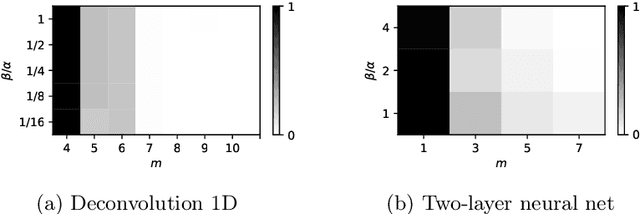
Sparse Optimization on Measures with Over-parameterized Gradient Descent

Minimizing a convex function of a measure with a sparsity-inducing penalty is a typical problem arising, e.g., in sparse spikes deconvolution or two-layer neural networks training. We show that this problem can be solved by discretizing the measure and running non-convex gradient descent on the positions and weights of the particles. For measures on a $d$-dimensional manifold and under some non-degeneracy assumptions, this leads to a global optimization algorithm with a complexity scaling as $\log(1/\epsilon)$ in the desired accuracy $\epsilon$, instead of $\epsilon^{-d}$ for convex methods. The key theoretical tools are a local convergence analysis in Wasserstein space and an analysis of a perturbed mirror descent in the space of measures. Our bounds involve quantities that are exponential in $d$ which is unavoidable under our assumptions.

A Note on Lazy Training in Supervised Differentiable Programming

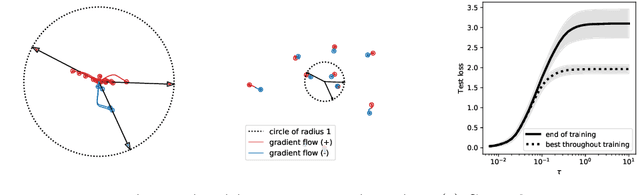
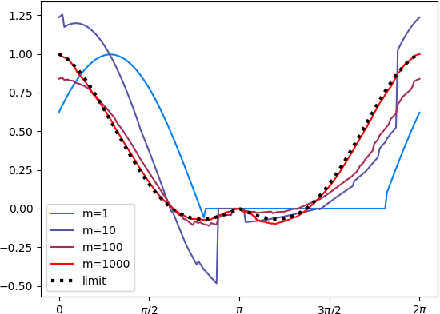
In a series of recent theoretical works, it has been shown that strongly over-parameterized neural networks trained with gradient-based methods could converge linearly to zero training loss, with their parameters hardly varying. In this note, our goal is to exhibit the simple structure that is behind these results. In a simplified setting, we prove that "lazy training" essentially solves a kernel regression. We also show that this behavior is not so much due to over-parameterization than to a choice of scaling, often implicit, that allows to linearize the model around its initialization. These theoretical results complemented with simple numerical experiments make it seem unlikely that "lazy training" is behind the many successes of neural networks in high dimensional tasks.

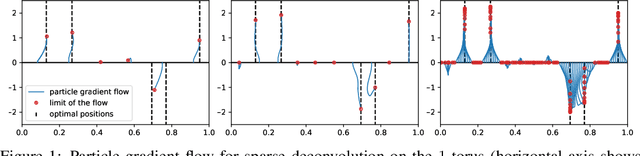
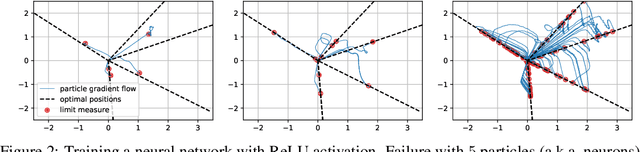
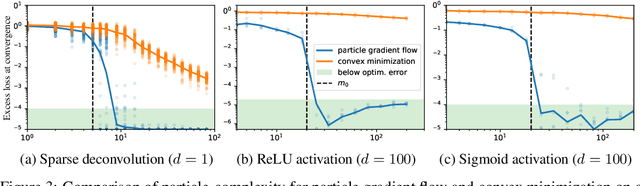
On the Global Convergence of Gradient Descent for Over-parameterized Models using Optimal Transport

Many tasks in machine learning and signal processing can be solved by minimizing a convex function of a measure. This includes sparse spikes deconvolution or training a neural network with a single hidden layer. For these problems, we study a simple minimization method: the unknown measure is discretized into a mixture of particles and a continuous-time gradient descent is performed on their weights and positions. This is an idealization of the usual way to train neural networks with a large hidden layer. We show that, when initialized correctly and in the many-particle limit, this gradient flow, although non-convex, converges to global minimizers. The proof involves Wasserstein gradient flows, a by-product of optimal transport theory. Numerical experiments show that this asymptotic behavior is already at play for a reasonable number of particles, even in high dimension.