Causal Climate Emulation with Bayesian Filtering

Traditional models of climate change use complex systems of coupled equations to simulate physical processes across the Earth system. These simulations are highly computationally expensive, limiting our predictions of climate change and analyses of its causes and effects. Machine learning has the potential to quickly emulate data from climate models, but current approaches are not able to incorporate physics-informed causal relationships. Here, we develop an interpretable climate model emulator based on causal representation learning. We derive a physics-informed approach including a Bayesian filter for stable long-term autoregressive emulation. We demonstrate that our emulator learns accurate climate dynamics, and we show the importance of each one of its components on a realistic synthetic dataset and data from two widely deployed climate models.

Towards Causal Representations of Climate Model Data

Climate models, such as Earth system models (ESMs), are crucial for simulating future climate change based on projected Shared Socioeconomic Pathways (SSP) greenhouse gas emissions scenarios. While ESMs are sophisticated and invaluable, machine learning-based emulators trained on existing simulation data can project additional climate scenarios much faster and are computationally efficient. However, they often lack generalizability and interpretability. This work delves into the potential of causal representation learning, specifically the \emph{Causal Discovery with Single-parent Decoding} (CDSD) method, which could render climate model emulation efficient \textit{and} interpretable. We evaluate CDSD on multiple climate datasets, focusing on emissions, temperature, and precipitation. Our findings shed light on the challenges, limitations, and promise of using CDSD as a stepping stone towards more interpretable and robust climate model emulation.

Learning interpretable continuous-time models of latent stochastic dynamical systems

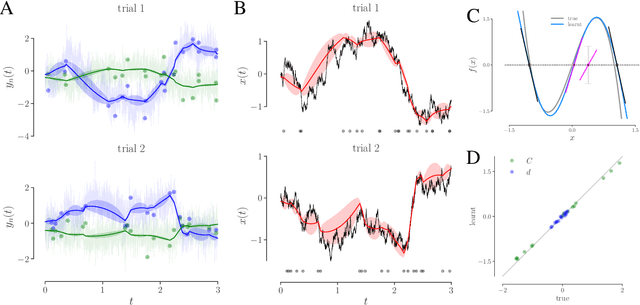
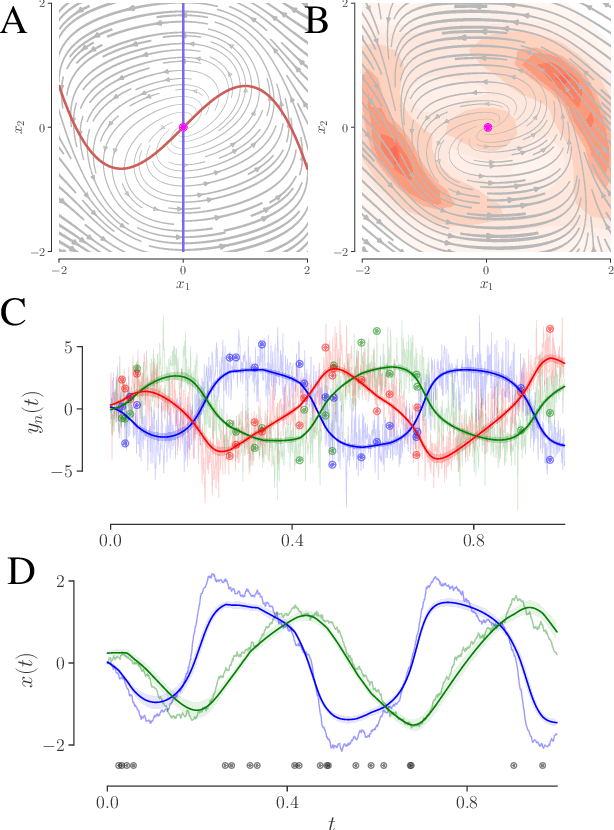
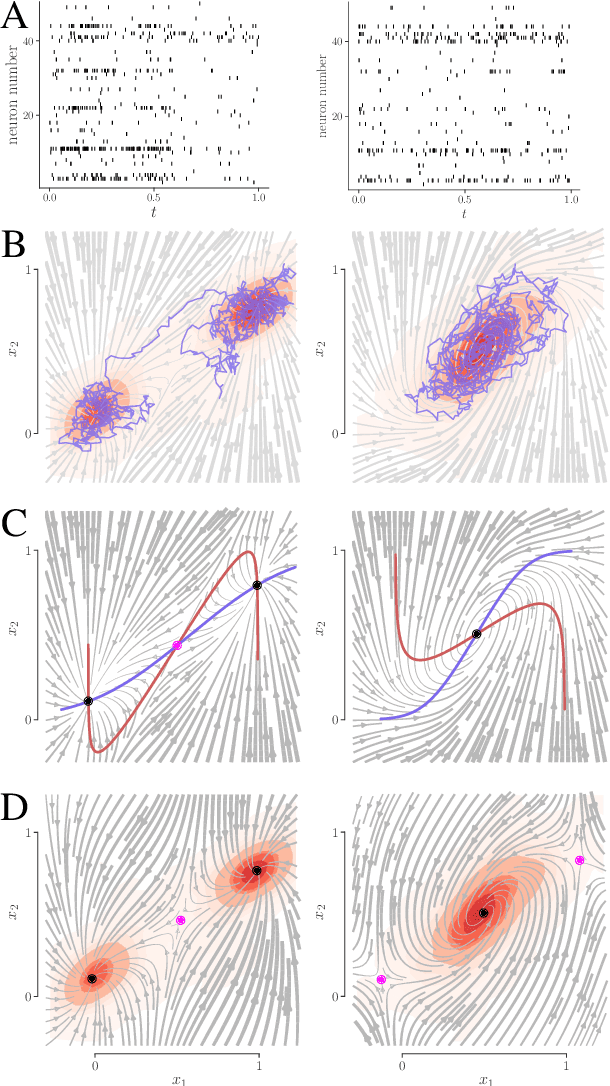
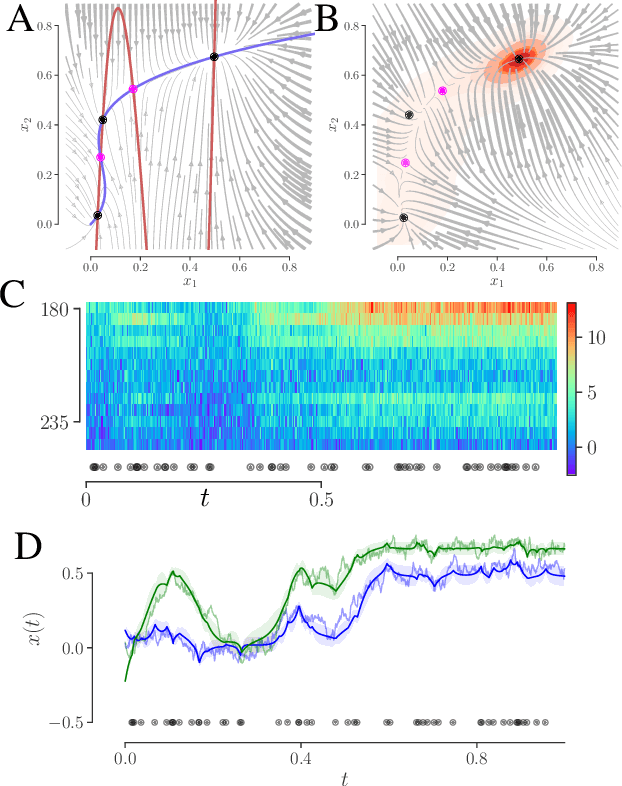
We develop an approach to learn an interpretable semi-parametric model of a latent continuous-time stochastic dynamical system, assuming noisy high-dimensional outputs sampled at uneven times. The dynamics are described by a nonlinear stochastic differential equation (SDE) driven by a Wiener process, with a drift evolution function drawn from a Gaussian process (GP) conditioned on a set of learnt fixed points and corresponding local Jacobian matrices. This form yields a flexible nonparametric model of the dynamics, with a representation corresponding directly to the interpretable portraits routinely employed in the study of nonlinear dynamical systems. The learning algorithm combines inference of continuous latent paths underlying observed data with a sparse variational description of the dynamical process. We demonstrate our approach on simulated data from different nonlinear dynamical systems.