Hyperspectral Super-Resolution with Inter-Image Variability via Degradation-based Low-Rank and Residual Fusion Method

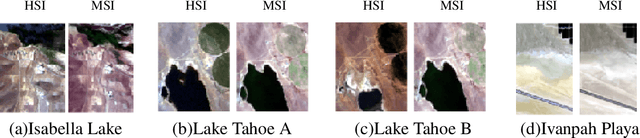
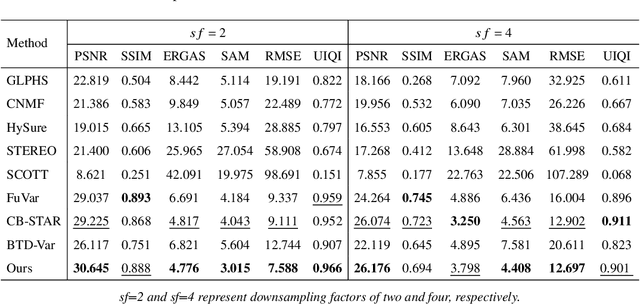
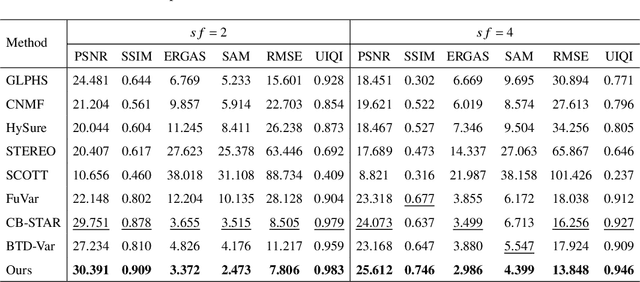
The fusion of hyperspectral image (HSI) with multispectral image (MSI) provides an effective way to enhance the spatial resolution of HSI. However, due to different acquisition conditions, there may exist spectral variability and spatially localized changes between HSI and MSI, referred to as inter-image variability, which can significantly affect the fusion performance. Existing methods typically handle inter-image variability by applying direct transformations to the images themselves, which can exacerbate the ill-posedness of the fusion model. To address this challenge, we propose a Degradation-based Low-Rank and Residual Fusion (DLRRF) model. First, we model the spectral variability as change in the spectral degradation operator. Second, to recover the lost spatial details caused by spatially localized changes, we decompose the target HSI into low rank and residual components, where the latter is used to capture the lost details. By exploiting the spectral correlation within the images, we perform dimensionality reduction on both components. Additionally, we introduce an implicit regularizer to utilize the spatial prior information from the images. The proposed DLRRF model is solved using the Proximal Alternating Optimization (PAO) algorithm within a Plug-and-Play (PnP) framework, where the subproblem regarding implicit regularizer is addressed by an external denoiser. We further provide a comprehensive convergence analysis of the algorithm. Finally, extensive numerical experiments demonstrate that DLRRF achieves superior performance in fusing HSI and MSI with inter-image variability.

MAUGIF: Mechanism-Aware Unsupervised General Image Fusion via Dual Cross-Image Autoencoders

Image fusion aims to integrate structural and complementary information from multi-source images. However, existing fusion methods are often either highly task-specific, or general frameworks that apply uniform strategies across diverse tasks, ignoring their distinct fusion mechanisms. To address this issue, we propose a mechanism-aware unsupervised general image fusion (MAUGIF) method based on dual cross-image autoencoders. Initially, we introduce a classification of additive and multiplicative fusion according to the inherent mechanisms of different fusion tasks. Then, dual encoders map source images into a shared latent space, capturing common content while isolating modality-specific details. During the decoding phase, dual decoders act as feature injectors, selectively reintegrating the unique characteristics of each modality into the shared content for reconstruction. The modality-specific features are injected into the source image in the fusion process, generating the fused image that integrates information from both modalities. The architecture of decoders varies according to their fusion mechanisms, enhancing both performance and interpretability. Extensive experiments are conducted on diverse fusion tasks to validate the effectiveness and generalization ability of our method. The code is available at https://anonymous.4open.science/r/MAUGIF.

A Hybrid Registration and Fusion Method for Hyperspectral Super-resolution

Fusing hyperspectral images (HSIs) with multispectral images (MSIs) has become a mainstream approach to enhance the spatial resolution of HSIs. Many HSI-MSI fusion methods have achieved impressive results. Nevertheless, certain challenges persist, including: (a) A majority of current methods rely on accurate registration of HSI and MSI, which can be challenging in real-world applications.(b) The obtained HSI-MSI pairs may not be fully utilized. In this paper, we propose a hybrid registration and fusion constrained optimization model named RAF-NLRGS. With respect to challenge (a), the RAF model integrates batch image alignment within the fusion process, facilitating simultaneous execution of image registration and fusion. To address issue (b), the NLRGS model incorporates a nonconvex low-rank and group-sparse structure, leveraging group sparsity to effectively harness valuable information embedded in the residual data. Moreover, the NLRGS model can further enhance fusion performance based on the RAF model. Subsequently, the RAF-NLRGS model is solved within the framework of Generalized Gauss-Newton (GGN) algorithm and Proximal Alternating Optimization (PAO) algorithm. Theoretically, we establish the error bounds for the NLRGS model and the convergence analysis of corresponding algorithms is also presented. Finally, extensive numerical experiments on HSI datasets are conducted to verify the effectiveness of our method.