Personalized Coupled Tensor Decomposition for Multimodal Data Fusion: Uniqueness and Algorithms

Coupled tensor decompositions (CTDs) perform data fusion by linking factors from different datasets. Although many CTDs have been already proposed, current works do not address important challenges of data fusion, where: 1) the datasets are often heterogeneous, constituting different "views" of a given phenomena (multimodality); and 2) each dataset can contain personalized or dataset-specific information, constituting distinct factors that are not coupled with other datasets. In this work, we introduce a personalized CTD framework tackling these challenges. A flexible model is proposed where each dataset is represented as the sum of two components, one related to a common tensor through a multilinear measurement model, and another specific to each dataset. Both the common and distinct components are assumed to admit a polyadic decomposition. This generalizes several existing CTD models. We provide conditions for specific and generic uniqueness of the decomposition that are easy to interpret. These conditions employ uni-mode uniqueness of different individual datasets and properties of the measurement model. Two algorithms are proposed to compute the common and distinct components: a semi-algebraic one and a coordinate-descent optimization method. Experimental results illustrate the advantage of the proposed framework compared with the state of the art approaches.

Coupled CP tensor decomposition with shared and distinct components for multi-task fMRI data fusion

Discovering components that are shared in multiple datasets, next to dataset-specific features, has great potential for studying the relationships between different subjects or tasks in functional Magnetic Resonance Imaging (fMRI) data. Coupled matrix and tensor factorization approaches have been useful for flexible data fusion, or decomposition to extract features that can be used in multiple ways. However, existing methods do not directly recover shared and dataset-specific components, which requires post-processing steps involving additional hyperparameter selection. In this paper, we propose a tensor-based framework for multi-task fMRI data fusion, using a partially constrained canonical polyadic (CP) decomposition model. Differently from previous approaches, the proposed method directly recovers shared and dataset-specific components, leading to results that are directly interpretable. A strategy to select a highly reproducible solution to the decomposition is also proposed. We evaluate the proposed methodology on real fMRI data of three tasks, and show that the proposed method finds meaningful components that clearly identify group differences between patients with schizophrenia and healthy controls.

Polarimetric phase retrieval: uniqueness and algorithms

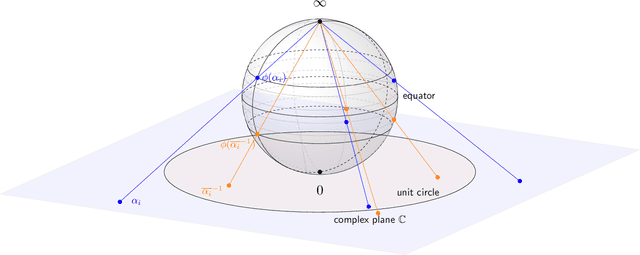
This work introduces a novel Fourier phase retrieval model, called polarimetric phase retrieval that enables a systematic use of polarization information in Fourier phase retrieval problems. We provide a complete characterization of uniqueness properties of this new model by unraveling equivalencies with a peculiar polynomial factorization problem. We introduce two different but complementary categories of reconstruction methods. The first one is algebraic and relies on the use of approximate greatest common divisor computations using Sylvester matrices. The second one carefully adapts existing algorithms for Fourier phase retrieval, namely semidefinite positive relaxation and Wirtinger-Flow, to solve the polarimetric phase retrieval problem. Finally, a set of numerical experiments permits a detailed assessment of the numerical behavior and relative performances of each proposed reconstruction strategy. We further highlight a reconstruction strategy that combines both approaches for scalable, computationally efficient and asymptotically MSE optimal performance.

Hankel low-rank approximation and completion in time series analysis and forecasting: a brief review

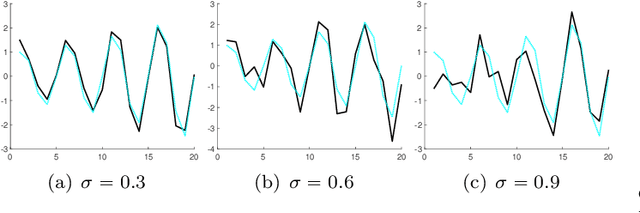
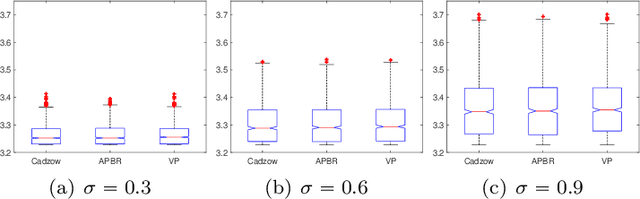
In this paper we offer a review and bibliography of work on Hankel low-rank approximation and completion, with particular emphasis on how this methodology can be used for time series analysis and forecasting. We begin by describing possible formulations of the problem and offer commentary on related topics and challenges in obtaining globally optimal solutions. Key theorems are provided, and the paper closes with some expository examples.

Low-rank tensor recovery for Jacobian-based Volterra identification of parallel Wiener-Hammerstein systems

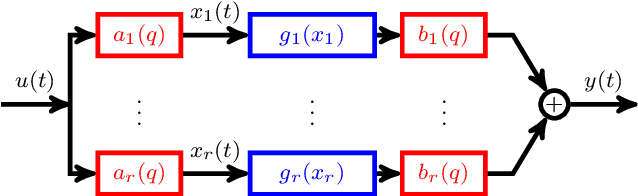
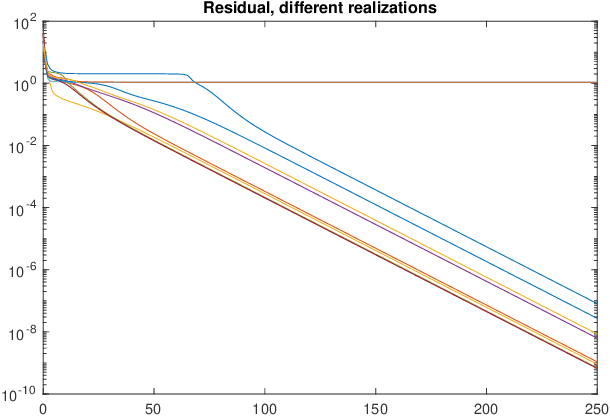
We consider the problem of identifying a parallel Wiener-Hammerstein structure from Volterra kernels. Methods based on Volterra kernels typically resort to coupled tensor decompositions of the kernels. However, in the case of parallel Wiener-Hammerstein systems, such methods require nontrivial constraints on the factors of the decompositions. In this paper, we propose an entirely different approach: by using special sampling (operating) points for the Jacobian of the nonlinear map from past inputs to the output, we can show that the Jacobian matrix becomes a linear projection of a tensor whose rank is equal to the number of branches. This representation allows us to solve the identification problem as a tensor recovery problem.

Tensor-based framework for training flexible neural networks

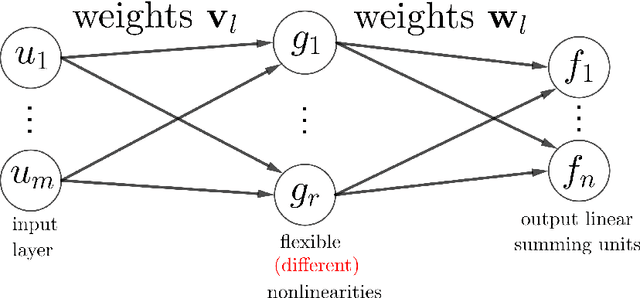
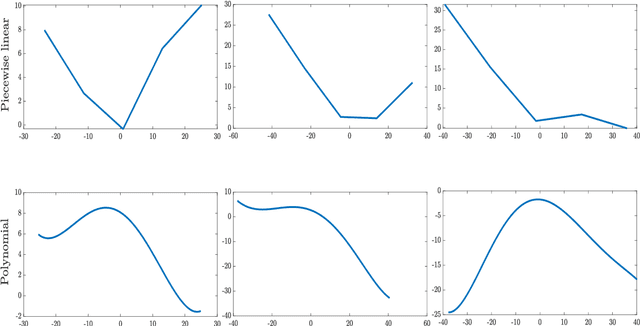
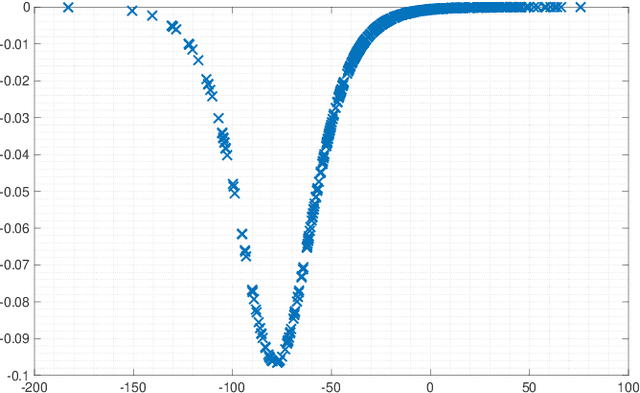
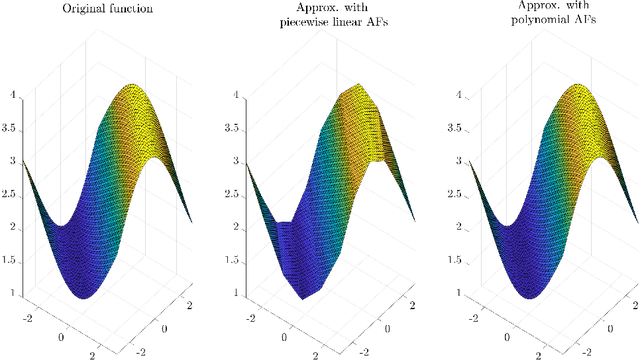
Activation functions (AFs) are an important part of the design of neural networks (NNs), and their choice plays a predominant role in the performance of a NN. In this work, we are particularly interested in the estimation of flexible activation functions using tensor-based solutions, where the AFs are expressed as a weighted sum of predefined basis functions. To do so, we propose a new learning algorithm which solves a constrained coupled matrix-tensor factorization (CMTF) problem. This technique fuses the first and zeroth order information of the NN, where the first-order information is contained in a Jacobian tensor, following a constrained canonical polyadic decomposition (CPD). The proposed algorithm can handle different decomposition bases. The goal of this method is to compress large pretrained NN models, by replacing subnetworks, {\em i.e.,} one or multiple layers of the original network, by a new flexible layer. The approach is applied to a pretrained convolutional neural network (CNN) used for character classification.

Structured low-rank matrix completion for forecasting in time series analysis

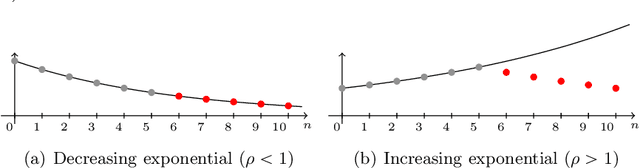
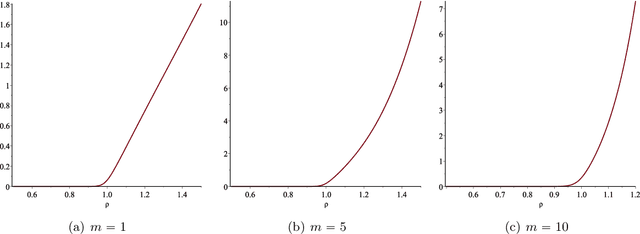
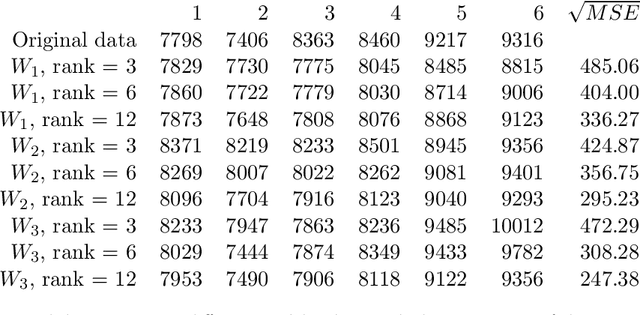
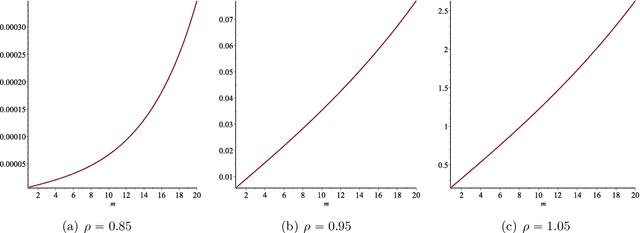
In this paper we consider the low-rank matrix completion problem with specific application to forecasting in time series analysis. Briefly, the low-rank matrix completion problem is the problem of imputing missing values of a matrix under a rank constraint. We consider a matrix completion problem for Hankel matrices and a convex relaxation based on the nuclear norm. Based on new theoretical results and a number of numerical and real examples, we investigate the cases when the proposed approach can work. Our results highlight the importance of choosing a proper weighting scheme for the known observations.

Identifiability of an X-rank decomposition of polynomial maps

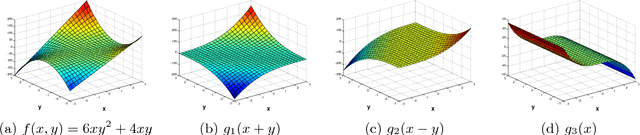
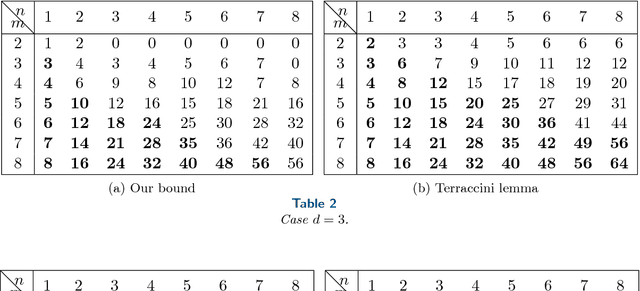
In this paper, we study a polynomial decomposition model that arises in problems of system identification, signal processing and machine learning. We show that this decomposition is a special case of the X-rank decomposition --- a powerful novel concept in algebraic geometry that generalizes the tensor CP decomposition. We prove new results on generic/maximal rank and on identifiability of a particular polynomial decomposition model. In the paper, we try to make results and basic tools accessible for general audience (assuming no knowledge of algebraic geometry or its prerequisites).

Adjusted least squares fitting of algebraic hypersurfaces

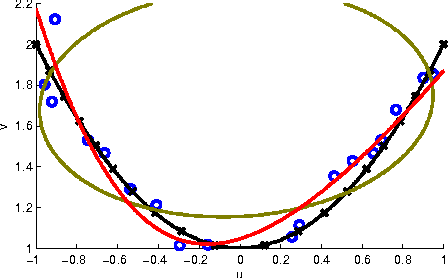
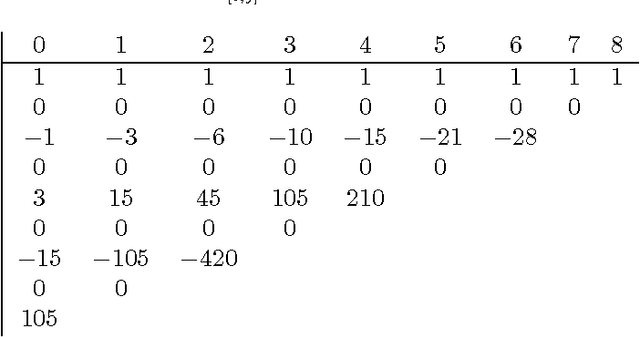
We consider the problem of fitting a set of points in Euclidean space by an algebraic hypersurface. We assume that points on a true hypersurface, described by a polynomial equation, are corrupted by zero mean independent Gaussian noise, and we estimate the coefficients of the true polynomial equation. The adjusted least squares estimator accounts for the bias present in the ordinary least squares estimator. The adjusted least squares estimator is based on constructing a quasi-Hankel matrix, which is a bias-corrected matrix of moments. For the case of unknown noise variance, the estimator is defined as a solution of a polynomial eigenvalue problem. In this paper, we present new results on invariance properties of the adjusted least squares estimator and an improved algorithm for computing the estimator for an arbitrary set of monomials in the polynomial equation.