Orthogonal Low Rank Embedding Stabilization

The instability of embedding spaces across model retraining cycles presents significant challenges to downstream applications using user or item embeddings derived from recommendation systems as input features. This paper introduces a novel orthogonal low-rank transformation methodology designed to stabilize the user/item embedding space, ensuring consistent embedding dimensions across retraining sessions. Our approach leverages a combination of efficient low-rank singular value decomposition and orthogonal Procrustes transformation to map embeddings into a standardized space. This transformation is computationally efficient, lossless, and lightweight, preserving the dot product and inference quality while reducing operational burdens. Unlike existing methods that modify training objectives or embedding structures, our approach maintains the integrity of the primary model application and can be seamlessly integrated with other stabilization techniques.

Multi-criteria Similarity-based Anomaly Detection using Pareto Depth Analysis

We consider the problem of identifying patterns in a data set that exhibit anomalous behavior, often referred to as anomaly detection. Similarity-based anomaly detection algorithms detect abnormally large amounts of similarity or dissimilarity, e.g.~as measured by nearest neighbor Euclidean distances between a test sample and the training samples. In many application domains there may not exist a single dissimilarity measure that captures all possible anomalous patterns. In such cases, multiple dissimilarity measures can be defined, including non-metric measures, and one can test for anomalies by scalarizing using a non-negative linear combination of them. If the relative importance of the different dissimilarity measures are not known in advance, as in many anomaly detection applications, the anomaly detection algorithm may need to be executed multiple times with different choices of weights in the linear combination. In this paper, we propose a method for similarity-based anomaly detection using a novel multi-criteria dissimilarity measure, the Pareto depth. The proposed Pareto depth analysis (PDA) anomaly detection algorithm uses the concept of Pareto optimality to detect anomalies under multiple criteria without having to run an algorithm multiple times with different choices of weights. The proposed PDA approach is provably better than using linear combinations of the criteria and shows superior performance on experiments with synthetic and real data sets.

Pareto-depth for Multiple-query Image Retrieval

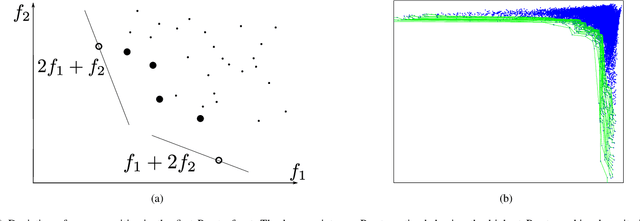
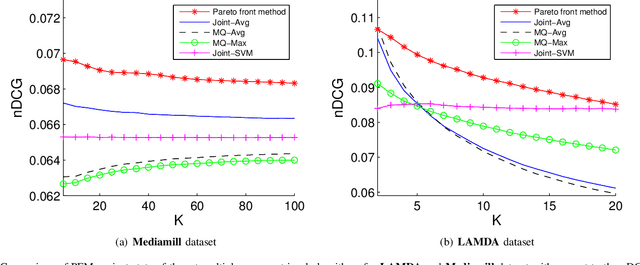
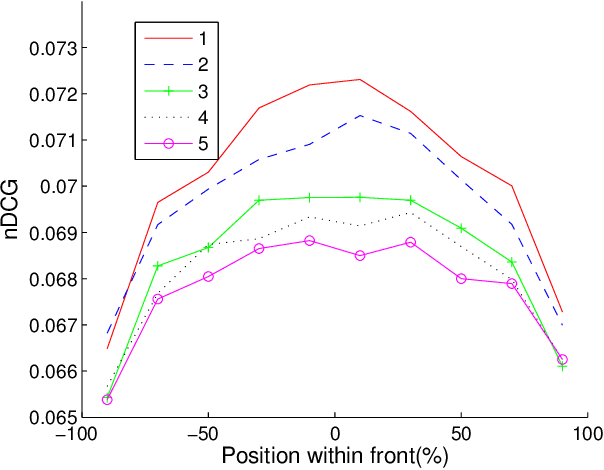
Most content-based image retrieval systems consider either one single query, or multiple queries that include the same object or represent the same semantic information. In this paper we consider the content-based image retrieval problem for multiple query images corresponding to different image semantics. We propose a novel multiple-query information retrieval algorithm that combines the Pareto front method (PFM) with efficient manifold ranking (EMR). We show that our proposed algorithm outperforms state of the art multiple-query retrieval algorithms on real-world image databases. We attribute this performance improvement to concavity properties of the Pareto fronts, and prove a theoretical result that characterizes the asymptotic concavity of the fronts.

Multi-criteria Anomaly Detection using Pareto Depth Analysis

We consider the problem of identifying patterns in a data set that exhibit anomalous behavior, often referred to as anomaly detection. In most anomaly detection algorithms, the dissimilarity between data samples is calculated by a single criterion, such as Euclidean distance. However, in many cases there may not exist a single dissimilarity measure that captures all possible anomalous patterns. In such a case, multiple criteria can be defined, and one can test for anomalies by scalarizing the multiple criteria using a linear combination of them. If the importance of the different criteria are not known in advance, the algorithm may need to be executed multiple times with different choices of weights in the linear combination. In this paper, we introduce a novel non-parametric multi-criteria anomaly detection method using Pareto depth analysis (PDA). PDA uses the concept of Pareto optimality to detect anomalies under multiple criteria without having to run an algorithm multiple times with different choices of weights. The proposed PDA approach scales linearly in the number of criteria and is provably better than linear combinations of the criteria.