A Dynamic Algorithm for Weighted Submodular Cover Problem

We initiate the study of the submodular cover problem in dynamic setting where the elements of the ground set are inserted and deleted. In the classical submodular cover problem, we are given a monotone submodular function $f : 2^{V} \to \mathbb{R}^{\ge 0}$ and the goal is to obtain a set $S \subseteq V$ that minimizes the cost subject to the constraint $f(S) = f(V)$. This is a classical problem in computer science and generalizes the Set Cover problem, 2-Set Cover, and dominating set problem among others. We consider this problem in a dynamic setting where there are updates to our set $V$, in the form of insertions and deletions of elements from a ground set $\mathcal{V}$, and the goal is to maintain an approximately optimal solution with low query complexity per update. For this problem, we propose a randomized algorithm that, in expectation, obtains a $(1-O(\epsilon), O(\epsilon^{-1}))$-bicriteria approximation using polylogarithmic query complexity per update.

Dynamic Non-monotone Submodular Maximization

Maximizing submodular functions has been increasingly used in many applications of machine learning, such as data summarization, recommendation systems, and feature selection. Moreover, there has been a growing interest in both submodular maximization and dynamic algorithms. In 2020, Monemizadeh and Lattanzi, Mitrovic, Norouzi{-}Fard, Tarnawski, and Zadimoghaddam initiated developing dynamic algorithms for the monotone submodular maximization problem under the cardinality constraint $k$. Recently, there have been some improvements on the topic made by Banihashem, Biabani, Goudarzi, Hajiaghayi, Jabbarzade, and Monemizadeh. In 2022, Chen and Peng studied the complexity of this problem and raised an important open question: "Can we extend [fully dynamic] results (algorithm or hardness) to non-monotone submodular maximization?". We affirmatively answer their question by demonstrating a reduction from maximizing a non-monotone submodular function under the cardinality constraint $k$ to maximizing a monotone submodular function under the same constraint. Through this reduction, we obtain the first dynamic algorithms to solve the non-monotone submodular maximization problem under the cardinality constraint $k$. Our algorithms maintain an $(8+\epsilon)$-approximate of the solution and use expected amortized $O(\epsilon^{-3}k^3\log^3(n)\log(k))$ or $O(\epsilon^{-1}k^2\log^3(k))$ oracle queries per update, respectively. Furthermore, we showcase the benefits of our dynamic algorithm for video summarization and max-cut problems on several real-world data sets.

An Improved Relaxation for Oracle-Efficient Adversarial Contextual Bandits

We present an oracle-efficient relaxation for the adversarial contextual bandits problem, where the contexts are sequentially drawn i.i.d from a known distribution and the cost sequence is chosen by an online adversary. Our algorithm has a regret bound of $O(T^{\frac{2}{3}}(K\log(|\Pi|))^{\frac{1}{3}})$ and makes at most $O(K)$ calls per round to an offline optimization oracle, where $K$ denotes the number of actions, $T$ denotes the number of rounds and $\Pi$ denotes the set of policies. This is the first result to improve the prior best bound of $O((TK)^{\frac{2}{3}}(\log(|\Pi|))^{\frac{1}{3}})$ as obtained by Syrgkanis et al. at NeurIPS 2016, and the first to match the original bound of Langford and Zhang at NeurIPS 2007 which was obtained for the stochastic case.

Dynamic Algorithms for Matroid Submodular Maximization

Submodular maximization under matroid and cardinality constraints are classical problems with a wide range of applications in machine learning, auction theory, and combinatorial optimization. In this paper, we consider these problems in the dynamic setting where (1) we have oracle access to a monotone submodular function $f: 2^{V} \rightarrow \mathbb{R}^+$ and (2) we are given a sequence $\mathcal{S}$ of insertions and deletions of elements of an underlying ground set $V$. We develop the first parameterized (by the rank $k$ of a matroid $\mathcal{M}$) dynamic $(4+\epsilon)$-approximation algorithm for the submodular maximization problem under the matroid constraint using an expected worst-case $O(k\log(k)\log^3{(k/\epsilon)})$ query complexity where $0 < \epsilon \le 1$. Chen and Peng at STOC'22 studied the complexity of this problem in the insertion-only dynamic model (a restricted version of the fully dynamic model where deletion is not allowed), and they raised the following important open question: *"for fully dynamic streams [sequences of insertions and deletions of elements], there is no known constant-factor approximation algorithm with poly(k) amortized queries for matroid constraints."* Our dynamic algorithm answers this question as well as an open problem of Lattanzi et al. (NeurIPS'20) affirmatively. As a byproduct, for the submodular maximization under the cardinality constraint $k$, we propose a parameterized (by the cardinality constraint $k$) dynamic algorithm that maintains a $(2+\epsilon)$-approximate solution of the sequence $\mathcal{S}$ at any time $t$ using the expected amortized worst-case complexity $O(k\epsilon^{-1}\log^2(k))$. This is the first dynamic algorithm for the problem that has a query complexity independent of the size of ground set $V$.

Optimal Sparse Recovery with Decision Stumps

Decision trees are widely used for their low computational cost, good predictive performance, and ability to assess the importance of features. Though often used in practice for feature selection, the theoretical guarantees of these methods are not well understood. We here obtain a tight finite sample bound for the feature selection problem in linear regression using single-depth decision trees. We examine the statistical properties of these "decision stumps" for the recovery of the $s$ active features from $p$ total features, where $s \ll p$. Our analysis provides tight sample performance guarantees on high-dimensional sparse systems which align with the finite sample bound of $O(s \log p)$ as obtained by Lasso, improving upon previous bounds for both the median and optimal splitting criteria. Our results extend to the non-linear regime as well as arbitrary sub-Gaussian distributions, demonstrating that tree based methods attain strong feature selection properties under a wide variety of settings and further shedding light on the success of these methods in practice. As a byproduct of our analysis, we show that we can provably guarantee recovery even when the number of active features $s$ is unknown. We further validate our theoretical results and proof methodology using computational experiments.

Bandit Social Learning: Exploration under Myopic Behavior

We study social learning dynamics where the agents collectively follow a simple multi-armed bandit protocol. Agents arrive sequentially, choose arms and receive associated rewards. Each agent observes the full history (arms and rewards) of the previous agents, and there are no private signals. While collectively the agents face exploration-exploitation tradeoff, each agent acts myopically, without regards to exploration. Motivating scenarios concern reviews and ratings on online platforms. We allow a wide range of myopic behaviors that are consistent with (parameterized) confidence intervals, including the "unbiased" behavior as well as various behaviorial biases. While extreme versions of these behaviors correspond to well-known bandit algorithms, we prove that more moderate versions lead to stark exploration failures, and consequently to regret rates that are linear in the number of agents. We provide matching upper bounds on regret by analyzing "moderately optimistic" agents. As a special case of independent interest, we obtain a general result on failure of the greedy algorithm in multi-armed bandits. This is the first such result in the literature, to the best of our knowledge

Run-Off Election: Improved Provable Defense against Data Poisoning Attacks

In data poisoning attacks, an adversary tries to change a model's prediction by adding, modifying, or removing samples in the training data. Recently, ensemble-based approaches for obtaining provable defenses against data poisoning have been proposed where predictions are done by taking a majority vote across multiple base models. In this work, we show that merely considering the majority vote in ensemble defenses is wasteful as it does not effectively utilize available information in the logits layers of the base models. Instead, we propose Run-Off Election (ROE), a novel aggregation method based on a two-round election across the base models: In the first round, models vote for their preferred class and then a second, Run-Off election is held between the top two classes in the first round. Based on this approach, we propose DPA+ROE and FA+ROE defense methods based on Deep Partition Aggregation (DPA) and Finite Aggregation (FA) approaches from prior work. We show how to obtain robustness for these methods using ideas inspired by dynamic programming and duality. We evaluate our methods on MNIST, CIFAR-10, and GTSRB and obtain improvements in certified accuracy by up to 4.73%, 3.63%, and 3.54%, respectively, establishing a new state-of-the-art in (pointwise) certified robustness against data poisoning. In many cases, our approach outperforms the state-of-the-art, even when using 32 times less computational power.

Explicit Tradeoffs between Adversarial and Natural Distributional Robustness

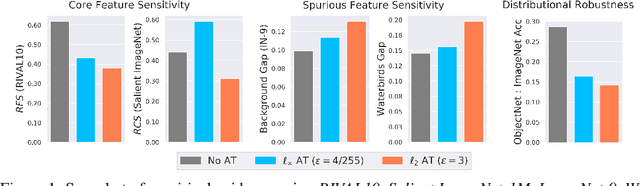
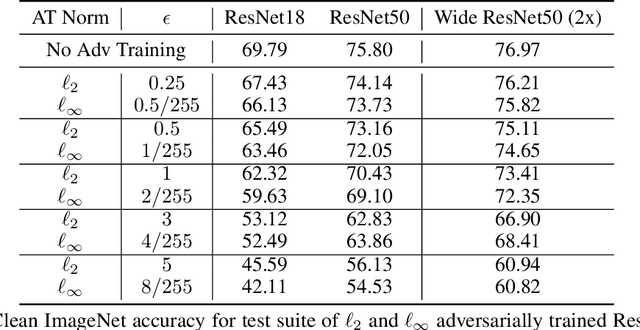
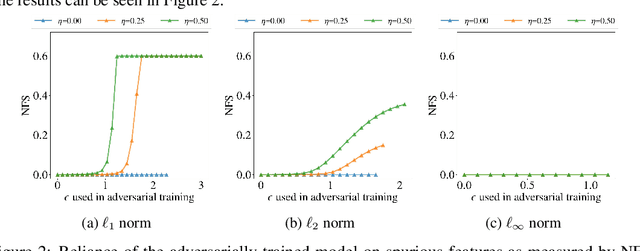
Several existing works study either adversarial or natural distributional robustness of deep neural networks separately. In practice, however, models need to enjoy both types of robustness to ensure reliability. In this work, we bridge this gap and show that in fact, explicit tradeoffs exist between adversarial and natural distributional robustness. We first consider a simple linear regression setting on Gaussian data with disjoint sets of core and spurious features. In this setting, through theoretical and empirical analysis, we show that (i) adversarial training with $\ell_1$ and $\ell_2$ norms increases the model reliance on spurious features; (ii) For $\ell_\infty$ adversarial training, spurious reliance only occurs when the scale of the spurious features is larger than that of the core features; (iii) adversarial training can have an unintended consequence in reducing distributional robustness, specifically when spurious correlations are changed in the new test domain. Next, we present extensive empirical evidence, using a test suite of twenty adversarially trained models evaluated on five benchmark datasets (ObjectNet, RIVAL10, Salient ImageNet-1M, ImageNet-9, Waterbirds), that adversarially trained classifiers rely on backgrounds more than their standardly trained counterparts, validating our theoretical results. We also show that spurious correlations in training data (when preserved in the test domain) can improve adversarial robustness, revealing that previous claims that adversarial vulnerability is rooted in spurious correlations are incomplete.

Admissible Policy Teaching through Reward Design

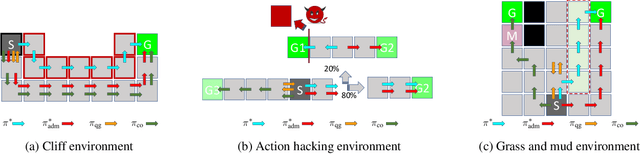
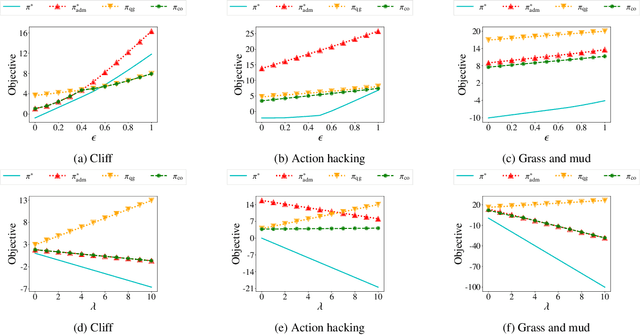
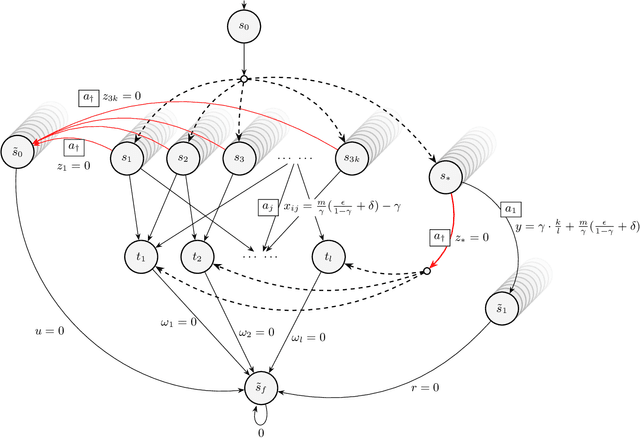
We study reward design strategies for incentivizing a reinforcement learning agent to adopt a policy from a set of admissible policies. The goal of the reward designer is to modify the underlying reward function cost-efficiently while ensuring that any approximately optimal deterministic policy under the new reward function is admissible and performs well under the original reward function. This problem can be viewed as a dual to the problem of optimal reward poisoning attacks: instead of forcing an agent to adopt a specific policy, the reward designer incentivizes an agent to avoid taking actions that are inadmissible in certain states. Perhaps surprisingly, and in contrast to the problem of optimal reward poisoning attacks, we first show that the reward design problem for admissible policy teaching is computationally challenging, and it is NP-hard to find an approximately optimal reward modification. We then proceed by formulating a surrogate problem whose optimal solution approximates the optimal solution to the reward design problem in our setting, but is more amenable to optimization techniques and analysis. For this surrogate problem, we present characterization results that provide bounds on the value of the optimal solution. Finally, we design a local search algorithm to solve the surrogate problem and showcase its utility using simulation-based experiments.

Defense Against Reward Poisoning Attacks in Reinforcement Learning

We study defense strategies against reward poisoning attacks in reinforcement learning. As a threat model, we consider attacks that minimally alter rewards to make the attacker's target policy uniquely optimal under the poisoned rewards, with the optimality gap specified by an attack parameter. Our goal is to design agents that are robust against such attacks in terms of the worst-case utility w.r.t. the true, unpoisoned, rewards while computing their policies under the poisoned rewards. We propose an optimization framework for deriving optimal defense policies, both when the attack parameter is known and unknown. Moreover, we show that defense policies that are solutions to the proposed optimization problems have provable performance guarantees. In particular, we provide the following bounds with respect to the true, unpoisoned, rewards: a) lower bounds on the expected return of the defense policies, and b) upper bounds on how suboptimal these defense policies are compared to the attacker's target policy. We conclude the paper by illustrating the intuitions behind our formal results, and showing that the derived bounds are non-trivial.