Bayesian Deconditional Kernel Mean Embeddings

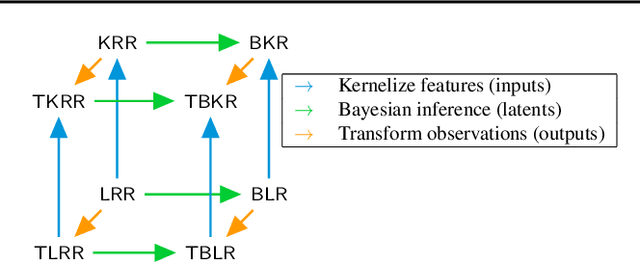
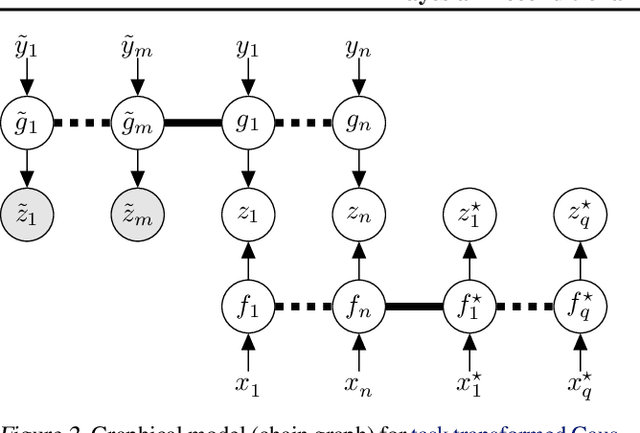
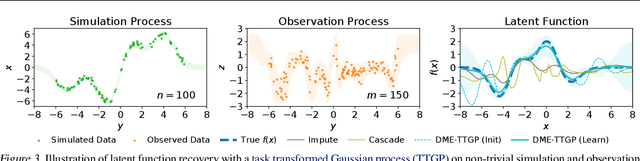
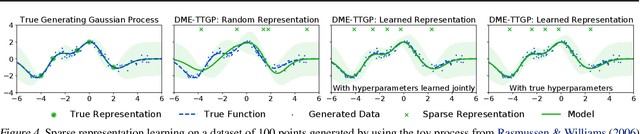
Conditional kernel mean embeddings form an attractive nonparametric framework for representing conditional means of functions, describing the observation processes for many complex models. However, the recovery of the original underlying function of interest whose conditional mean was observed is a challenging inference task. We formalize deconditional kernel mean embeddings as a solution to this inverse problem, and show that it can be naturally viewed as a nonparametric Bayes' rule. Critically, we introduce the notion of task transformed Gaussian processes and establish deconditional kernel means as their posterior predictive mean. This connection provides Bayesian interpretations and uncertainty estimates for deconditional kernel mean embeddings, explains their regularization hyperparameters, and reveals a marginal likelihood for kernel hyperparameter learning. These revelations further enable practical applications such as likelihood-free inference and learning sparse representations for big data.

Bayesian Learning of Conditional Kernel Mean Embeddings for Automatic Likelihood-Free Inference

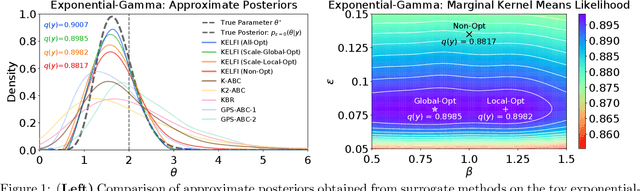
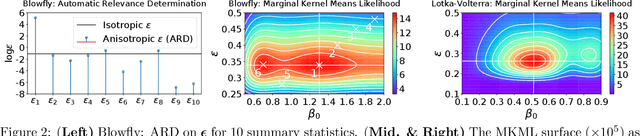
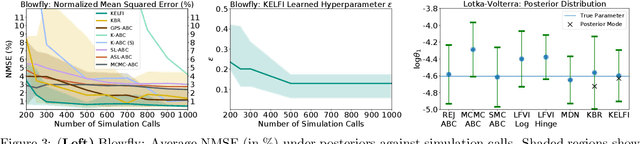
In likelihood-free settings where likelihood evaluations are intractable, approximate Bayesian computation (ABC) addresses the formidable inference task to discover plausible parameters of simulation programs that explain the observations. However, they demand large quantities of simulation calls. Critically, hyperparameters that determine measures of simulation discrepancy crucially balance inference accuracy and sample efficiency, yet are difficult to tune. In this paper, we present kernel embedding likelihood-free inference (KELFI), a holistic framework that automatically learns model hyperparameters to improve inference accuracy given limited simulation budget. By leveraging likelihood smoothness with conditional mean embeddings, we nonparametrically approximate likelihoods and posteriors as surrogate densities and sample from closed-form posterior mean embeddings, whose hyperparameters are learned under its approximate marginal likelihood. Our modular framework demonstrates improved accuracy and efficiency on challenging inference problems in ecology.

Hyperparameter Learning for Conditional Mean Embeddings with Rademacher Complexity Bounds

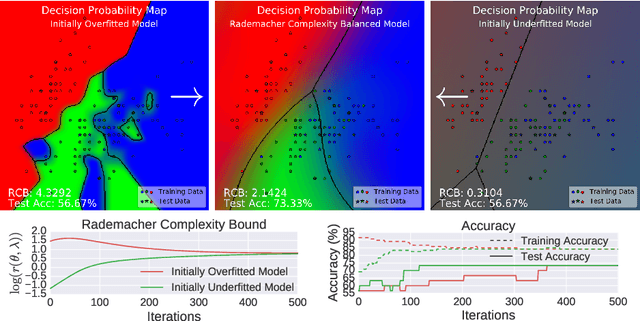
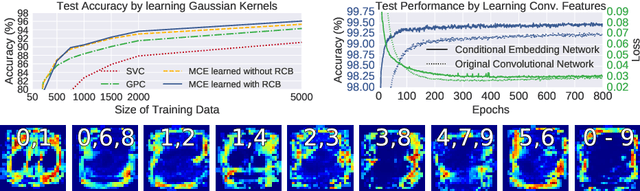
Conditional mean embeddings are nonparametric models that encode conditional expectations in a reproducing kernel Hilbert space. While they provide a flexible and powerful framework for probabilistic inference, their performance is highly dependent on the choice of kernel and regularization hyperparameters. Nevertheless, current hyperparameter tuning methods predominantly rely on expensive cross validation or heuristics that is not optimized for the inference task. For conditional mean embeddings with categorical targets and arbitrary inputs, we propose a hyperparameter learning framework based on Rademacher complexity bounds to prevent overfitting by balancing data fit against model complexity. Our approach only requires batch updates, allowing scalable kernel hyperparameter tuning without invoking kernel approximations. Experiments demonstrate that our learning framework outperforms competing methods, and can be further extended to incorporate and learn deep neural network weights to improve generalization.