Online Mirror Descent for Tchebycheff Scalarization in Multi-Objective Optimization

The goal of multi-objective optimization (MOO) is to learn under multiple, potentially conflicting, objectives. One widely used technique to tackle MOO is through linear scalarization, where one fixed preference vector is used to combine the objectives into a single scalar value for optimization. However, recent work (Hu et al., 2024) has shown linear scalarization often fails to capture the non-convex regions of the Pareto Front, failing to recover the complete set of Pareto optimal solutions. In light of the above limitations, this paper focuses on Tchebycheff scalarization that optimizes for the worst-case objective. In particular, we propose an online mirror descent algorithm for Tchebycheff scalarization, which we call OMD-TCH. We show that OMD-TCH enjoys a convergence rate of $O(\sqrt{\log m/T})$ where $m$ is the number of objectives and $T$ is the number of iteration rounds. We also propose a novel adaptive online-to-batch conversion scheme that significantly improves the practical performance of OMD-TCH while maintaining the same convergence guarantees. We demonstrate the effectiveness of OMD-TCH and the adaptive conversion scheme on both synthetic problems and federated learning tasks under fairness constraints, showing state-of-the-art performance.

Impact of Decentralized Learning on Player Utilities in Stackelberg Games

When deployed in the world, a learning agent such as a recommender system or a chatbot often repeatedly interacts with another learning agent (such as a user) over time. In many such two-agent systems, each agent learns separately and the rewards of the two agents are not perfectly aligned. To better understand such cases, we examine the learning dynamics of the two-agent system and the implications for each agent's objective. We model these systems as Stackelberg games with decentralized learning and show that standard regret benchmarks (such as Stackelberg equilibrium payoffs) result in worst-case linear regret for at least one player. To better capture these systems, we construct a relaxed regret benchmark that is tolerant to small learning errors by agents. We show that standard learning algorithms fail to provide sublinear regret, and we develop algorithms to achieve near-optimal $O(T^{2/3})$ regret for both players with respect to these benchmarks. We further design relaxed environments under which faster learning ($O(\sqrt{T})$) is possible. Altogether, our results take a step towards assessing how two-agent interactions in sequential and decentralized learning environments affect the utility of both agents.

When Are Two Lists Better than One?: Benefits and Harms in Joint Decision-making

Historically, much of machine learning research has focused on the performance of the algorithm alone, but recently more attention has been focused on optimizing joint human-algorithm performance. Here, we analyze a specific type of human-algorithm collaboration where the algorithm has access to a set of $n$ items, and presents a subset of size $k$ to the human, who selects a final item from among those $k$. This scenario could model content recommendation, route planning, or any type of labeling task. Because both the human and algorithm have imperfect, noisy information about the true ordering of items, the key question is: which value of $k$ maximizes the probability that the best item will be ultimately selected? For $k=1$, performance is optimized by the algorithm acting alone, and for $k=n$ it is optimized by the human acting alone. Surprisingly, we show that for multiple of noise models, it is optimal to set $k \in [2, n-1]$ - that is, there are strict benefits to collaborating, even when the human and algorithm have equal accuracy separately. We demonstrate this theoretically for the Mallows model and experimentally for the Random Utilities models of noisy permutations. However, we show this pattern is reversed when the human is anchored on the algorithm's presented ordering - the joint system always has strictly worse performance. We extend these results to the case where the human and algorithm differ in their accuracy levels, showing that there always exist regimes where a more accurate agent would strictly benefit from collaborating with a less accurate one, but these regimes are asymmetric between the human and the algorithm's accuracy.

Human-Algorithm Collaboration: Achieving Complementarity and Avoiding Unfairness

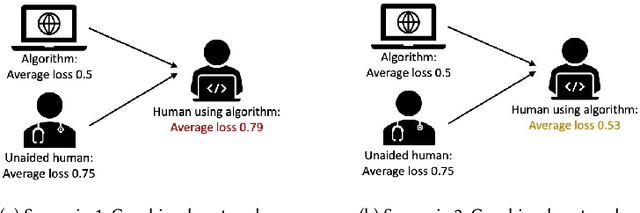
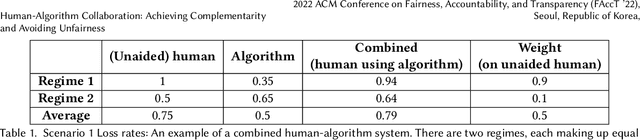
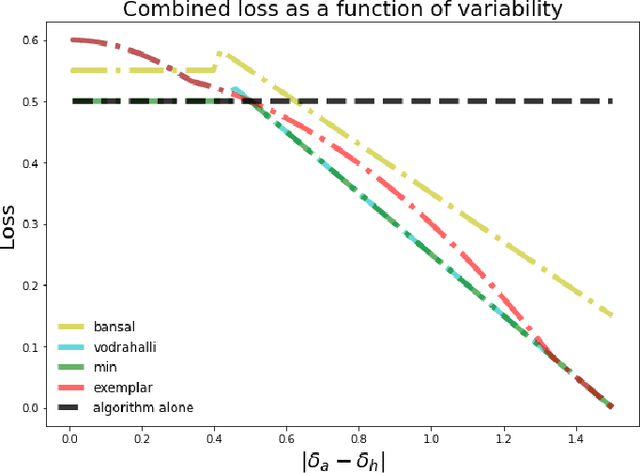
Much of machine learning research focuses on predictive accuracy: given a task, create a machine learning model (or algorithm) that maximizes accuracy. In many settings, however, the final prediction or decision of a system is under the control of a human, who uses an algorithm's output along with their own personal expertise in order to produce a combined prediction. One ultimate goal of such collaborative systems is "complementarity": that is, to produce lower loss (equivalently, greater payoff or utility) than either the human or algorithm alone. However, experimental results have shown that even in carefully-designed systems, complementary performance can be elusive. Our work provides three key contributions. First, we provide a theoretical framework for modeling simple human-algorithm systems and demonstrate that multiple prior analyses can be expressed within it. Next, we use this model to prove conditions where complementarity is impossible, and give constructive examples of where complementarity is achievable. Finally, we discuss the implications of our findings, especially with respect to the fairness of a classifier. In sum, these results deepen our understanding of key factors influencing the combined performance of human-algorithm systems, giving insight into how algorithmic tools can best be designed for collaborative environments.

Models of fairness in federated learning

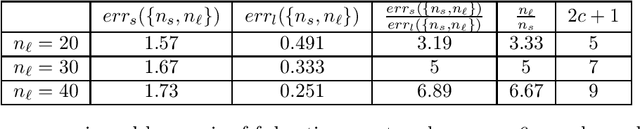
In many real-world situations, data is distributed across multiple locations and can't be combined for training. Federated learning is a novel distributed learning approach that allows multiple federating agents to jointly learn a model. While this approach might reduce the error each agent experiences, it also raises questions of fairness: to what extent can the error experienced by one agent be significantly lower than the error experienced by another agent? In this work, we consider two notions of fairness that each may be appropriate in different circumstances: "egalitarian fairness" (which aims to bound how dissimilar error rates can be) and "proportional fairness" (which aims to reward players for contributing more data). For egalitarian fairness, we obtain a tight multiplicative bound on how widely error rates can diverge between agents federating together. For proportional fairness, we show that sub-proportional error (relative to the number of data points contributed) is guaranteed for any individually rational federating coalition.

Optimality and Stability in Federated Learning: A Game-theoretic Approach

Federated learning is a distributed learning paradigm where multiple agents, each only with access to local data, jointly learn a global model. There has recently been an explosion of research aiming not only to improve the accuracy rates of federated learning, but also provide certain guarantees around social good properties such as total error. One branch of this research has taken a game-theoretic approach, and in particular, prior work has viewed federated learning as a hedonic game, where error-minimizing players arrange themselves into federating coalitions. This past work proves the existence of stable coalition partitions, but leaves open a wide range of questions, including how far from optimal these stable solutions are. In this work, we motivate and define a notion of optimality given by the average error rates among federating agents (players). First, we provide and prove the correctness of an efficient algorithm to calculate an optimal (error minimizing) arrangement of players. Next, we analyze the relationship between the stability and optimality of an arrangement. First, we show that for some regions of parameter space, all stable arrangements are optimal (Price of Anarchy equal to 1). However, we show this is not true for all settings: there exist examples of stable arrangements with higher cost than optimal (Price of Anarchy greater than 1). Finally, we give the first constant-factor bound on the performance gap between stability and optimality, proving that the total error of the worst stable solution can be no higher than 9 times the total error of an optimal solution (Price of Anarchy bound of 9).

Model-sharing Games: Analyzing Federated Learning Under Voluntary Participation

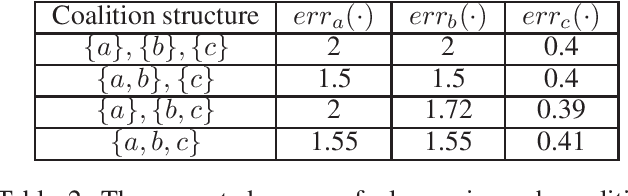
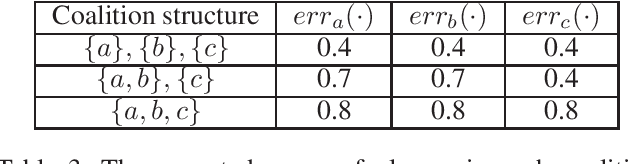
Federated learning is a setting where agents, each with access to their own data source, combine models learned from local data to create a global model. If agents are drawing their data from different distributions, though, federated learning might produce a biased global model that is not optimal for each agent. This means that agents face a fundamental question: should they join the global model or stay with their local model? In this work, we show how this situation can be naturally analyzed through the framework of coalitional game theory. Motivated by these considerations, we propose the following game: there are heterogeneous players with different model parameters governing their data distribution and different amounts of data they have noisily drawn from their own distribution. Each player's goal is to obtain a model with minimal expected mean squared error (MSE) on their own distribution. They have a choice of fitting a model based solely on their own data, or combining their learned parameters with those of some subset of the other players. Combining models reduces the variance component of their error through access to more data, but increases the bias because of the heterogeneity of distributions. In this work, we derive exact expected MSE values for problems in linear regression and mean estimation. We use these values to analyze the resulting game in the framework of hedonic game theory; we study how players might divide into coalitions, where each set of players within a coalition jointly constructs a single model. In a case with arbitrarily many players that each have either a "small" or "large" amount of data, we constructively show that there always exists a stable partition of players into coalitions.