Scaling Up Collaborative Filtering Data Sets through Randomized Fractal Expansions

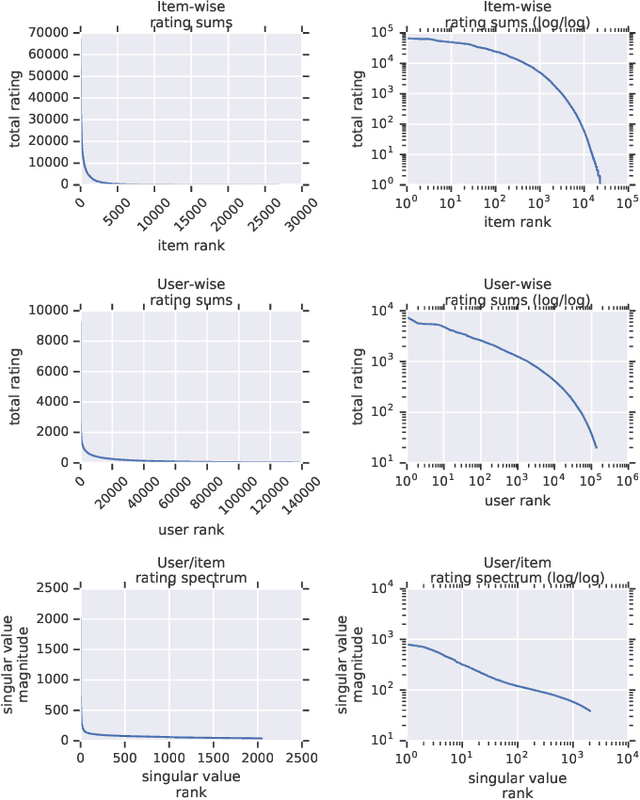
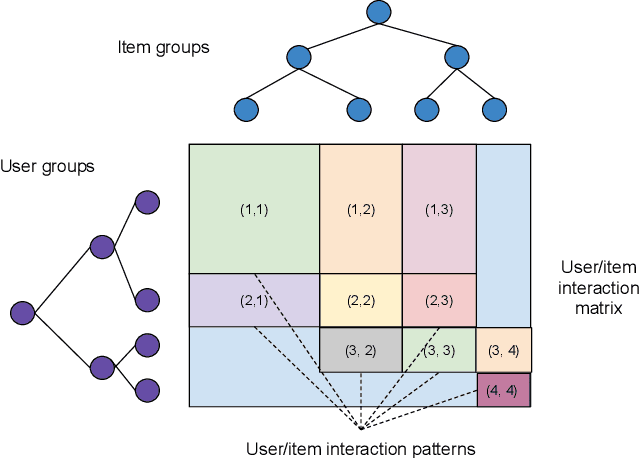
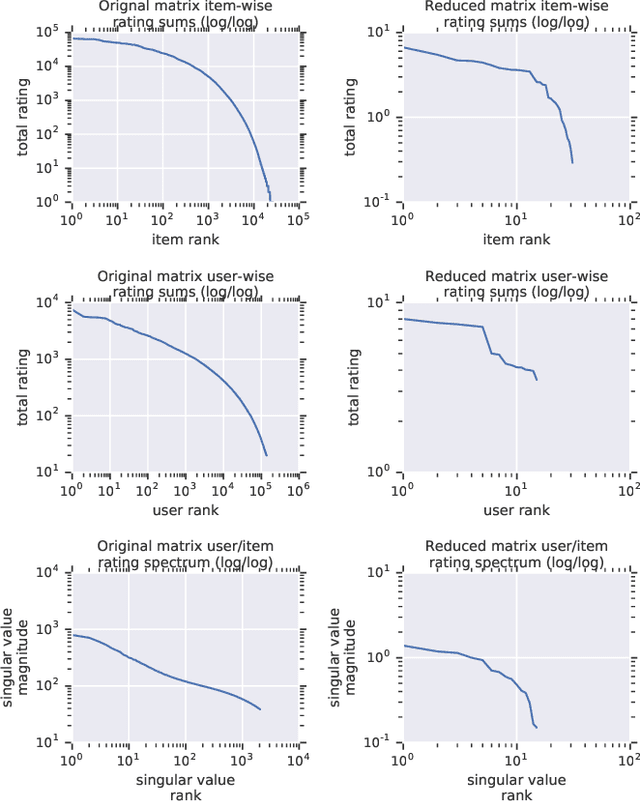
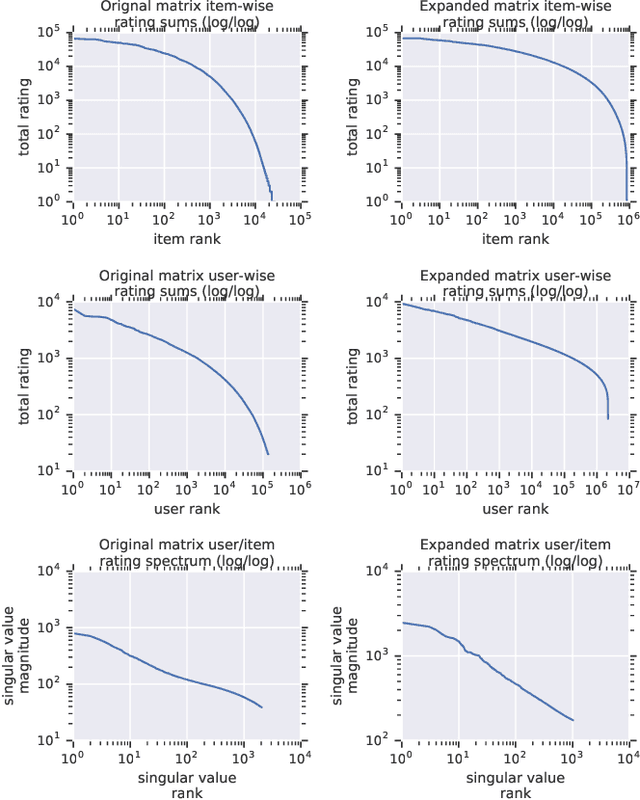
Recommender system research suffers from a disconnect between the size of academic data sets and the scale of industrial production systems. In order to bridge that gap, we propose to generate large-scale user/item interaction data sets by expanding pre-existing public data sets. Our key contribution is a technique that expands user/item incidence matrices matrices to large numbers of rows (users), columns (items), and non-zero values (interactions). The proposed method adapts Kronecker Graph Theory to preserve key higher order statistical properties such as the fat-tailed distribution of user engagements, item popularity, and singular value spectra of user/item interaction matrices. Preserving such properties is key to building large realistic synthetic data sets which in turn can be employed reliably to benchmark recommender systems and the systems employed to train them. We further apply our stochastic expansion algorithm to the binarized MovieLens 20M data set, which comprises 20M interactions between 27K movies and 138K users. The resulting expanded data set has 1.2B ratings, 2.2M users, and 855K items, which can be scaled up or down.

Scalable Realistic Recommendation Datasets through Fractal Expansions

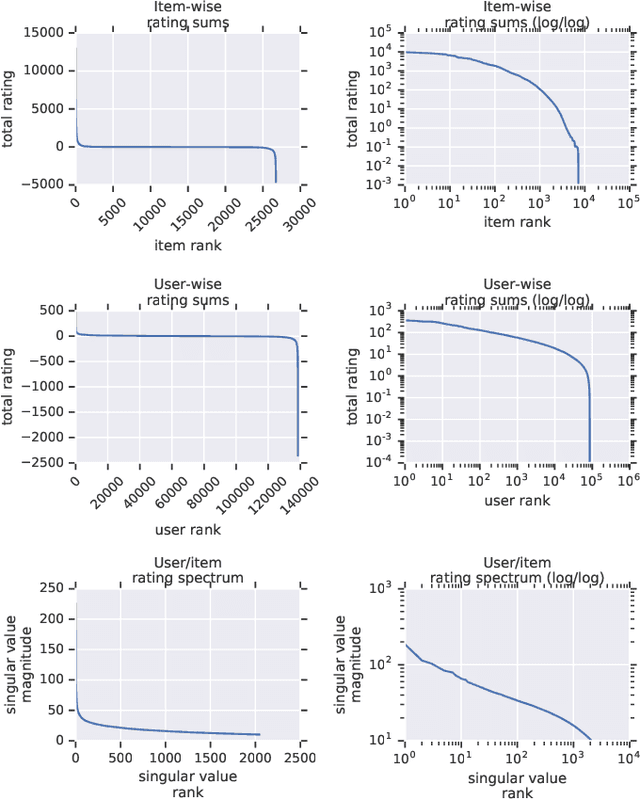
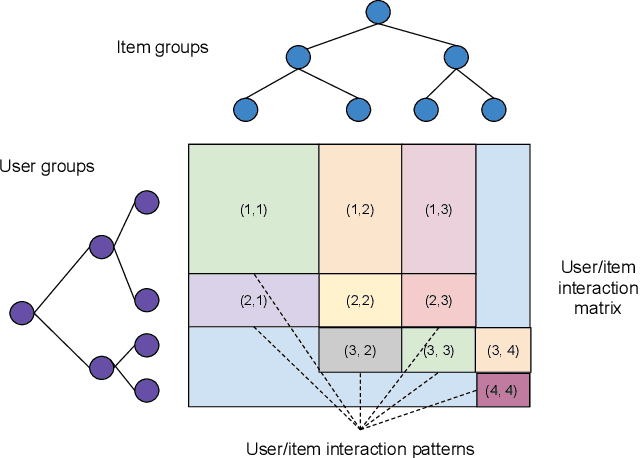
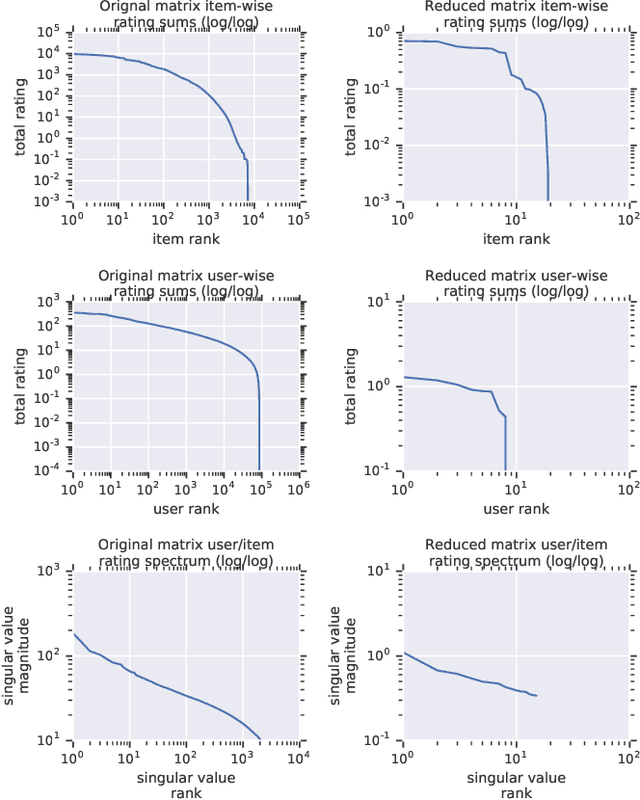
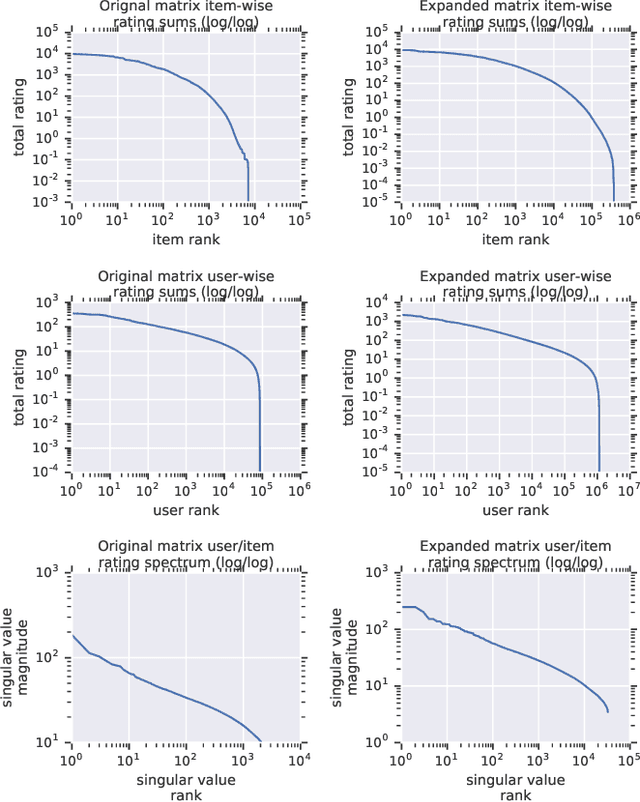
Recommender System research suffers currently from a disconnect between the size of academic data sets and the scale of industrial production systems. In order to bridge that gap we propose to generate more massive user/item interaction data sets by expanding pre-existing public data sets. User/item incidence matrices record interactions between users and items on a given platform as a large sparse matrix whose rows correspond to users and whose columns correspond to items. Our technique expands such matrices to larger numbers of rows (users), columns (items) and non zero values (interactions) while preserving key higher order statistical properties. We adapt the Kronecker Graph Theory to user/item incidence matrices and show that the corresponding fractal expansions preserve the fat-tailed distributions of user engagements, item popularity and singular value spectra of user/item interaction matrices. Preserving such properties is key to building large realistic synthetic data sets which in turn can be employed reliably to benchmark Recommender Systems and the systems employed to train them. We provide algorithms to produce such expansions and apply them to the MovieLens 20 million data set comprising 20 million ratings of 27K movies by 138K users. The resulting expanded data set has 10 billion ratings, 2 million items and 864K users in its smaller version and can be scaled up or down. A larger version features 655 billion ratings, 7 million items and 17 million users.