Kajal De
Achieving greater Explanatory Power and Forecasting Accuracy with Non-uniform spread Fuzzy Linear Regression
Jul 07, 2013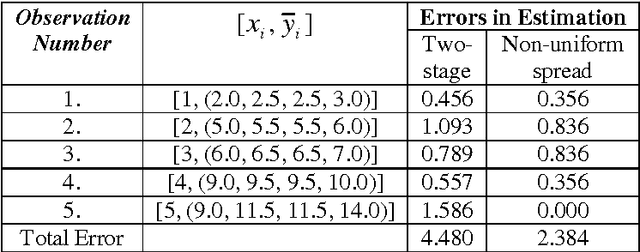
Abstract:Fuzzy regression models have been applied to several Operations Research applications viz., forecasting and prediction. Earlier works on fuzzy regression analysis obtain crisp regression coefficients for eliminating the problem of increasing spreads for the estimated fuzzy responses as the magnitude of the independent variable increases. But they cannot deal with the problem of non-uniform spreads. In this work, a three-phase approach is discussed to construct the fuzzy regression model with non-uniform spreads to deal with this problem. The first phase constructs the membership functions of the least-squares estimates of regression coefficients based on extension principle to completely conserve the fuzziness of observations. They are then defuzzified by the centre of area method to obtain crisp regression coefficients in the second phase. Finally, the error terms of the method are determined by setting each estimated spread equal to its corresponding observed spread. The Tagaki-Sugeno inference system is used for improving the accuracy of forecasts. The simulation example demonstrates the strength of fuzzy linear regression model in terms of higher explanatory power and forecasting performance.
Fuzzy Integer Linear Programming Mathematical Models for Examination Timetable Problem
Jul 07, 2013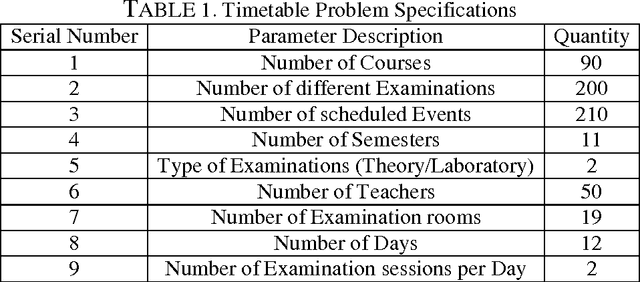
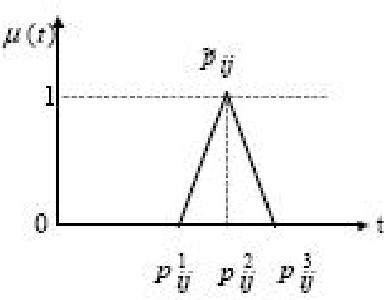
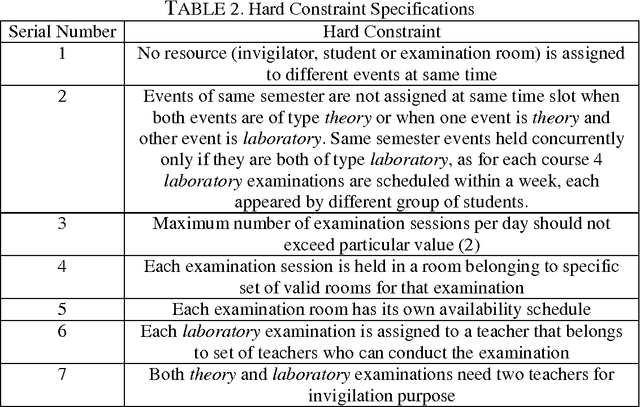
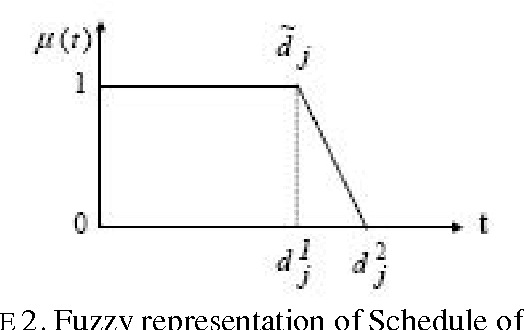
Abstract:ETP is NP Hard combinatorial optimization problem. It has received tremendous research attention during the past few years given its wide use in universities. In this Paper, we develop three mathematical models for NSOU, Kolkata, India using FILP technique. To deal with impreciseness and vagueness we model various allocation variables through fuzzy numbers. The solution to the problem is obtained using Fuzzy number ranking method. Each feasible solution has fuzzy number obtained by Fuzzy objective function. The different FILP technique performance are demonstrated by experimental data generated through extensive simulation from NSOU, Kolkata, India in terms of its execution times. The proposed FILP models are compared with commonly used heuristic viz. ILP approach on experimental data which gives an idea about quality of heuristic. The techniques are also compared with different Artificial Intelligence based heuristics for ETP with respect to best and mean cost as well as execution time measures on Carter benchmark datasets to illustrate its effectiveness. FILP takes an appreciable amount of time to generate satisfactory solution in comparison to other heuristics. The formulation thus serves as good benchmark for other heuristics. The experimental study presented here focuses on producing a methodology that generalizes well over spectrum of techniques that generates significant results for one or more datasets. The performance of FILP model is finally compared to the best results cited in literature for Carter benchmarks to assess its potential. The problem can be further reduced by formulating with lesser number of allocation variables it without affecting optimality of solution obtained. FLIP model for ETP can also be adapted to solve other ETP as well as combinatorial optimization problems.
Discovering Stock Price Prediction Rules of Bombay Stock Exchange Using Rough Fuzzy Multi Layer Perception Networks
Jul 07, 2013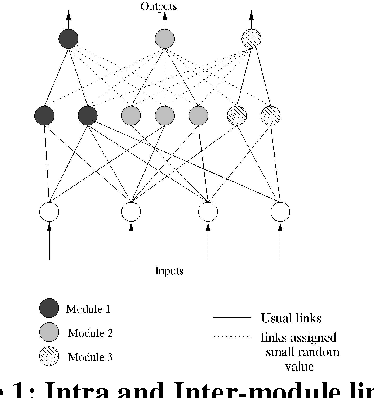
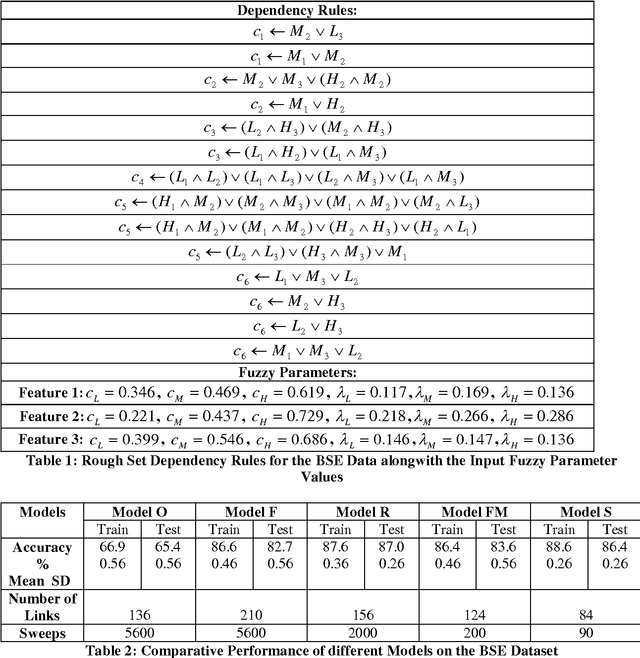
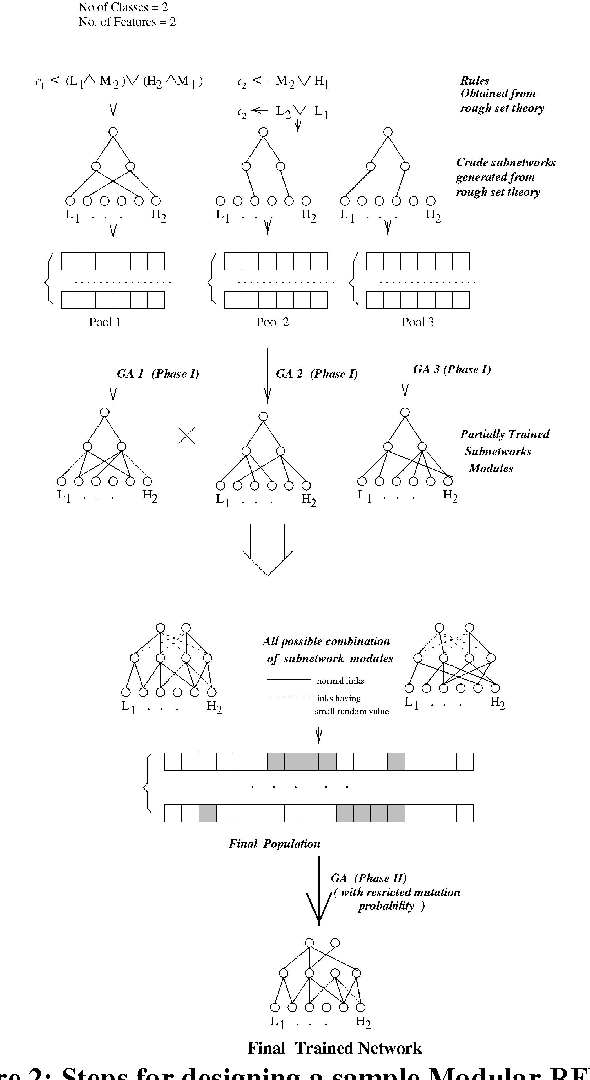
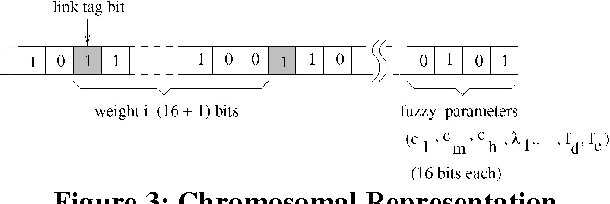
Abstract:In India financial markets have existed for many years. A functionally accented, diverse, efficient and flexible financial system is vital to the national objective of creating a market driven, productive and competitive economy. Today markets of varying maturity exist in equity, debt, commodities and foreign exchange. In this work we attempt to generate prediction rules scheme for stock price movement at Bombay Stock Exchange using an important Soft Computing paradigm viz., Rough Fuzzy Multi Layer Perception. The use of Computational Intelligence Systems such as Neural Networks, Fuzzy Sets, Genetic Algorithms, etc. for Stock Market Predictions has been widely established. The process is to extract knowledge in the form of rules from daily stock movements. These rules can then be used to guide investors. To increase the efficiency of the prediction process, Rough Sets is used to discretize the data. The methodology uses a Genetic Algorithm to obtain a structured network suitable for both classification and rule extraction. The modular concept, based on divide and conquer strategy, provides accelerated training and a compact network suitable for generating a minimum number of rules with high certainty values. The concept of variable mutation operator is introduced for preserving the localized structure of the constituting Knowledge Based sub-networks, while they are integrated and evolved. Rough Set Dependency Rules are generated directly from the real valued attribute table containing Fuzzy membership values. The paradigm is thus used to develop a rule extraction algorithm. The extracted rules are compared with some of the related rule extraction techniques on the basis of some quantitative performance indices. The proposed methodology extracts rules which are less in number, are accurate, have high certainty factor and have low confusion with less computation time.
Trapezoidal Fuzzy Numbers for the Transportation Problem
Jul 07, 2013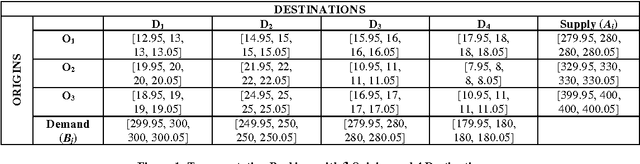
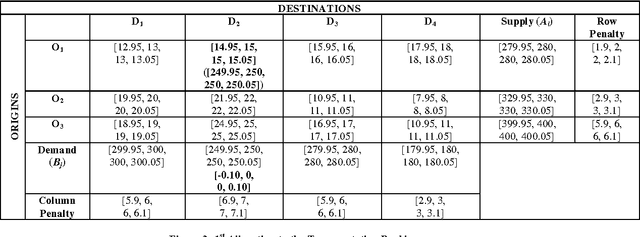
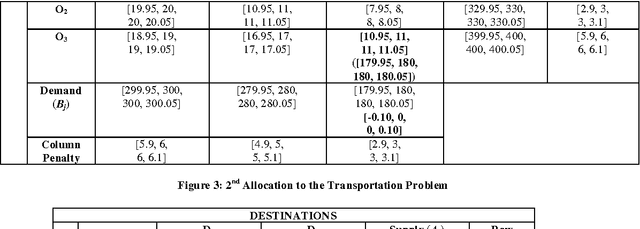
Abstract:Transportation Problem is an important problem which has been widely studied in Operations Research domain. It has been often used to simulate different real life problems. In particular, application of this Problem in NP Hard Problems has a remarkable significance. In this Paper, we present the closed, bounded and non empty feasible region of the transportation problem using fuzzy trapezoidal numbers which ensures the existence of an optimal solution to the balanced transportation problem. The multivalued nature of Fuzzy Sets allows handling of uncertainty and vagueness involved in the cost values of each cells in the transportation table. For finding the initial solution of the transportation problem we use the Fuzzy Vogel Approximation Method and for determining the optimality of the obtained solution Fuzzy Modified Distribution Method is used. The fuzzification of the cost of the transportation problem is discussed with the help of a numerical example. Finally, we discuss the computational complexity involved in the problem. To the best of our knowledge, this is the first work on obtaining the solution of the transportation problem using fuzzy trapezoidal numbers.
A Comparative study of Transportation Problem under Probabilistic and Fuzzy Uncertainties
Jul 07, 2013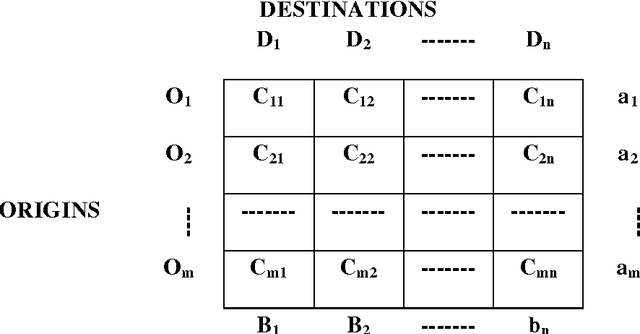
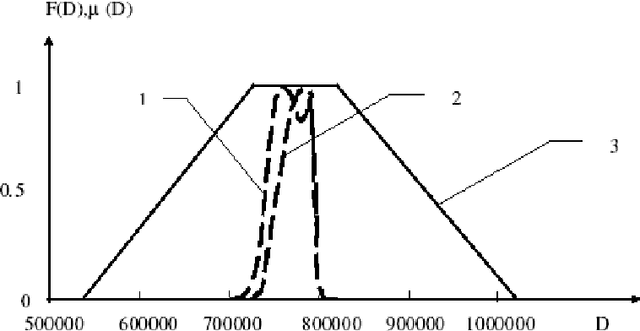
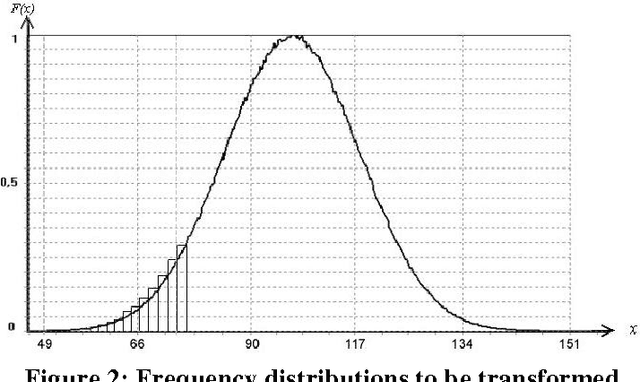
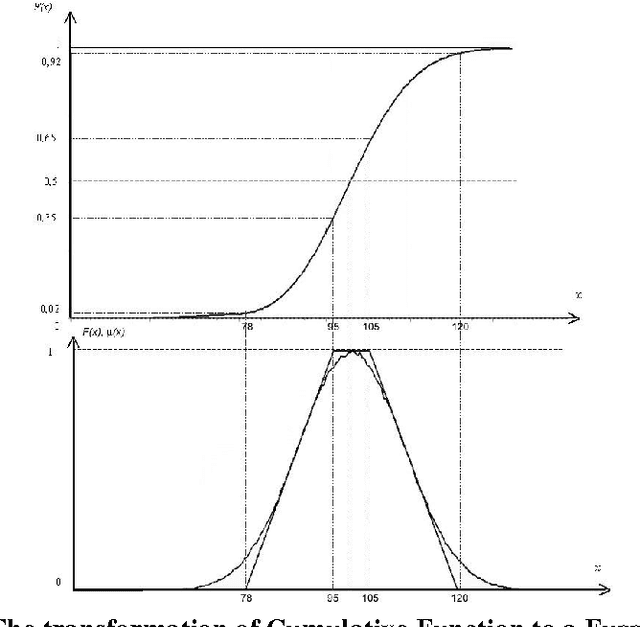
Abstract:Transportation Problem is an important aspect which has been widely studied in Operations Research domain. It has been studied to simulate different real life problems. In particular, application of this Problem in NP- Hard Problems has a remarkable significance. In this Paper, we present a comparative study of Transportation Problem through Probabilistic and Fuzzy Uncertainties. Fuzzy Logic is a computational paradigm that generalizes classical two-valued logic for reasoning under uncertainty. In order to achieve this, the notation of membership in a set needs to become a matter of degree. By doing this we accomplish two things viz., (i) ease of describing human knowledge involving vague concepts and (ii) enhanced ability to develop cost-effective solution to real-world problem. The multi-valued nature of Fuzzy Sets allows handling uncertain and vague information. It is a model-less approach and a clever disguise of Probability Theory. We give comparative simulation results of both approaches and discuss the Computational Complexity. To the best of our knowledge, this is the first work on comparative study of Transportation Problem using Probabilistic and Fuzzy Uncertainties.
Solution of System of Linear Equations - A Neuro-Fuzzy Approach
Apr 26, 2013Abstract:Neuro-Fuzzy Modeling has been applied in a wide variety of fields such as Decision Making, Engineering and Management Sciences etc. In particular, applications of this Modeling technique in Decision Making by involving complex Systems of Linear Algebraic Equations have remarkable significance. In this Paper, we present Polak-Ribiere Conjugate Gradient based Neural Network with Fuzzy rules to solve System of Simultaneous Linear Algebraic Equations. This is achieved using Fuzzy Backpropagation Learning Rule. The implementation results show that the proposed Neuro-Fuzzy Network yields effective solutions for exactly determined, underdetermined and over-determined Systems of Linear Equations. This fact is demonstrated by the Computational Complexity analysis of the Neuro-Fuzzy Algorithm. The proposed Algorithm is simulated effectively using MATLAB software. To the best of our knowledge this is the first work of the Systems of Linear Algebraic Equations using Neuro-Fuzzy Modeling.
Solution of the Decision Making Problems using Fuzzy Soft Relations
Apr 26, 2013
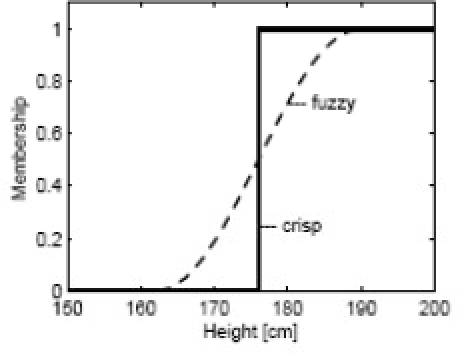
Abstract:The Fuzzy Modeling has been applied in a wide variety of fields such as Engineering and Management Sciences and Social Sciences to solve a number Decision Making Problems which involve impreciseness, uncertainty and vagueness in data. In particular, applications of this Modeling technique in Decision Making Problems have remarkable significance. These problems have been tackled using various theories such as Probability theory, Fuzzy Set Theory, Rough Set Theory, Vague Set Theory, Approximate Reasoning Theory etc. which lack in parameterization of the tools due to which they could not be applied successfully to such problems. The concept of Soft Set has a promising potential for giving an optimal solution for these problems. With the motivation of this new concept, in this paper we define the concepts of Soft Relation and Fuzzy Soft Relation and then apply them to solve a number of Decision Making Problems. The advantages of Fuzzy Soft Relation compared to other paradigms are discussed. To the best of our knowledge this is the first work on the application of Fuzzy Soft Relation to the Decision Making Problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge