Dipak Chatterjee
Fuzzy Mixed Integer Linear Programming for Air Vehicles Operations Optimization
Mar 13, 2015Abstract:Multiple Air Vehicles (AVs) to prosecute geographically dispersed targets is an important optimization problem. Associated multiple tasks viz., target classification, attack and verification are successively performed on each target. The optimal minimum time performance of these tasks requires cooperation among vehicles such that critical time constraints are satisfied i.e. target must be classified before it can be attacked and AV is sent to target area to verify its destruction after target has been attacked. Here, optimal task scheduling problem from Indian Air Force is formulated as Fuzzy Mixed Integer Linear Programming (FMILP) problem. The solution assigns all tasks to vehicles and performs scheduling in an optimal manner including scheduled staged departure times. Coupled tasks involving time and task order constraints are addressed. When AVs have sufficient endurance, existence of optimal solution is guaranteed. The solution developed can serve as an effective heuristic for different categories of AV optimization problems.
Fuzzy Mixed Integer Optimization Model for Regression Approach
Mar 13, 2015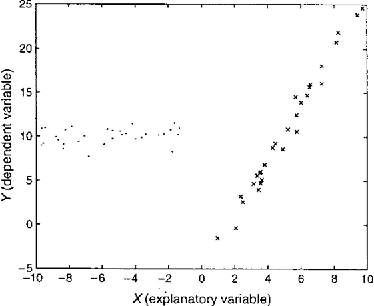
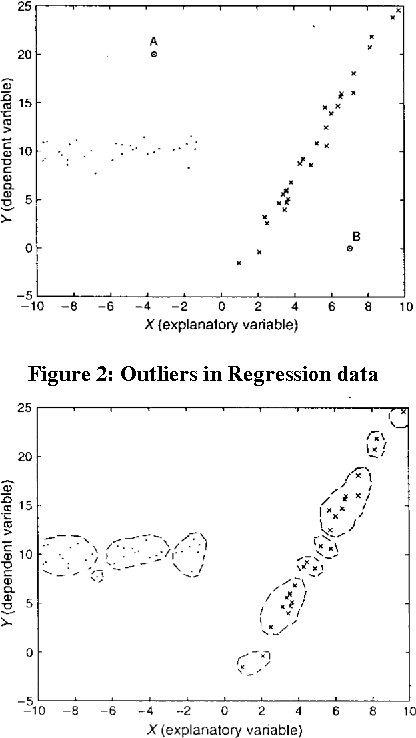
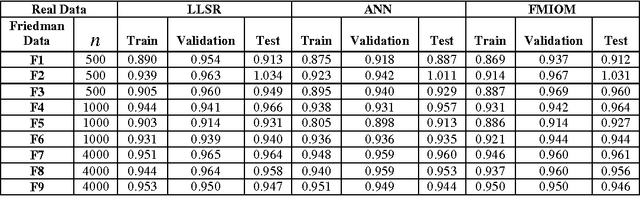
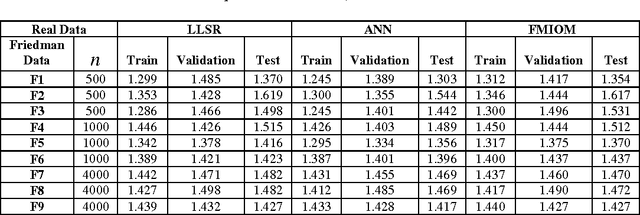
Abstract:Mixed Integer Optimization has been a topic of active research in past decades. It has been used to solve Statistical problems of classification and regression involving massive data. However, there is an inherent degree of vagueness present in huge real life data. This impreciseness is handled by Fuzzy Sets. In this Paper, Fuzzy Mixed Integer Optimization Method (FMIOM) is used to find solution to Regression problem. The methodology exploits discrete character of problem. In this way large scale problems are solved within practical limits. The data points are separated into different polyhedral regions and each region has its own distinct regression coefficients. In this attempt, an attention is drawn to Statistics and Data Mining community that Integer Optimization can be significantly used to revisit different Statistical problems. Computational experimentations with generated and real data sets show that FMIOM is comparable to and often outperforms current leading methods. The results illustrate potential for significant impact of Fuzzy Integer Optimization methods on Computational Statistics and Data Mining.
Discovering Stock Price Prediction Rules of Bombay Stock Exchange Using Rough Fuzzy Multi Layer Perception Networks
Jul 07, 2013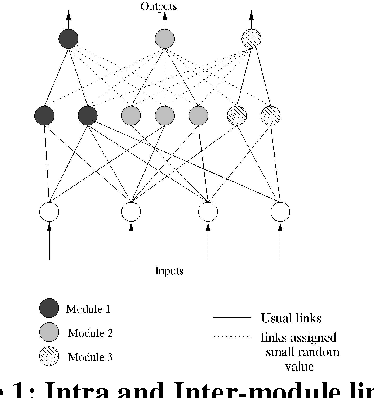
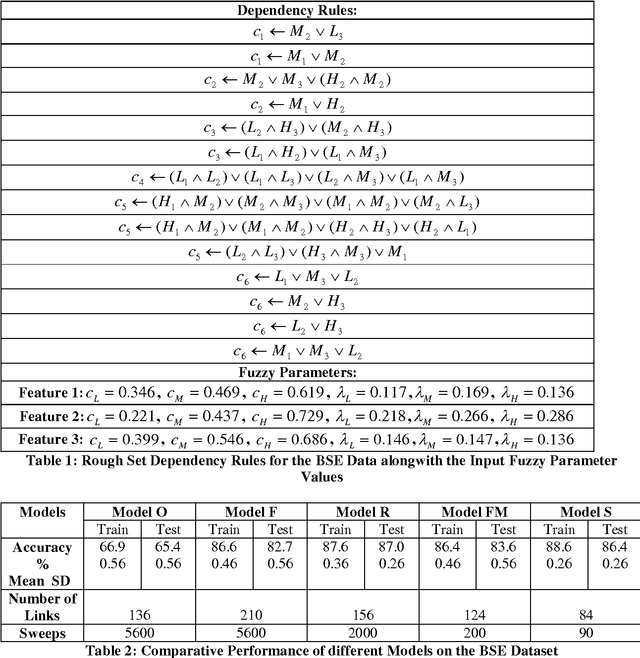
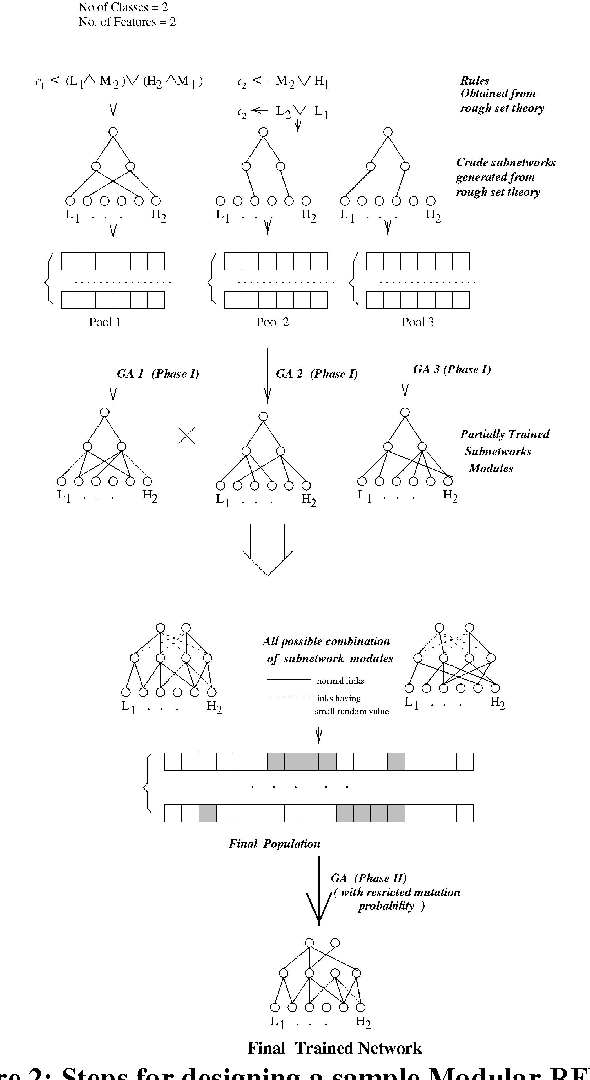
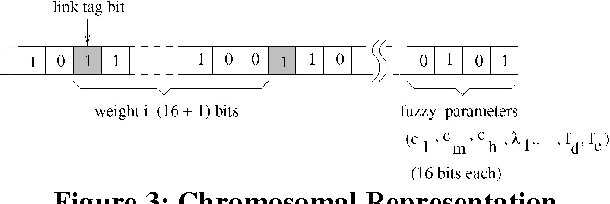
Abstract:In India financial markets have existed for many years. A functionally accented, diverse, efficient and flexible financial system is vital to the national objective of creating a market driven, productive and competitive economy. Today markets of varying maturity exist in equity, debt, commodities and foreign exchange. In this work we attempt to generate prediction rules scheme for stock price movement at Bombay Stock Exchange using an important Soft Computing paradigm viz., Rough Fuzzy Multi Layer Perception. The use of Computational Intelligence Systems such as Neural Networks, Fuzzy Sets, Genetic Algorithms, etc. for Stock Market Predictions has been widely established. The process is to extract knowledge in the form of rules from daily stock movements. These rules can then be used to guide investors. To increase the efficiency of the prediction process, Rough Sets is used to discretize the data. The methodology uses a Genetic Algorithm to obtain a structured network suitable for both classification and rule extraction. The modular concept, based on divide and conquer strategy, provides accelerated training and a compact network suitable for generating a minimum number of rules with high certainty values. The concept of variable mutation operator is introduced for preserving the localized structure of the constituting Knowledge Based sub-networks, while they are integrated and evolved. Rough Set Dependency Rules are generated directly from the real valued attribute table containing Fuzzy membership values. The paradigm is thus used to develop a rule extraction algorithm. The extracted rules are compared with some of the related rule extraction techniques on the basis of some quantitative performance indices. The proposed methodology extracts rules which are less in number, are accurate, have high certainty factor and have low confusion with less computation time.
Trapezoidal Fuzzy Numbers for the Transportation Problem
Jul 07, 2013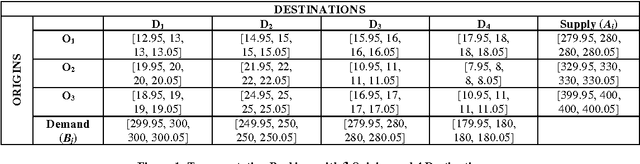
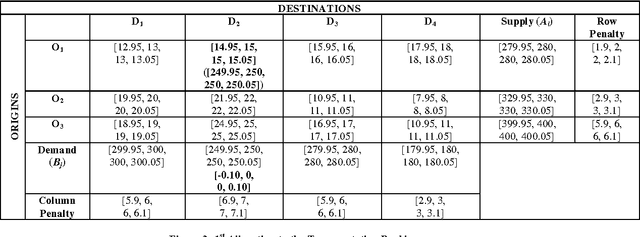
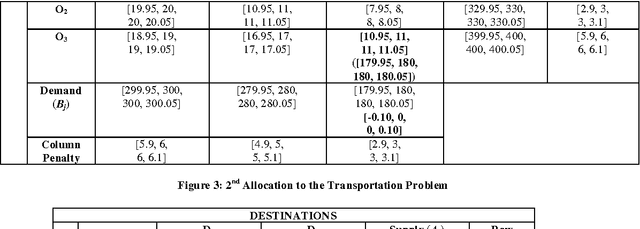
Abstract:Transportation Problem is an important problem which has been widely studied in Operations Research domain. It has been often used to simulate different real life problems. In particular, application of this Problem in NP Hard Problems has a remarkable significance. In this Paper, we present the closed, bounded and non empty feasible region of the transportation problem using fuzzy trapezoidal numbers which ensures the existence of an optimal solution to the balanced transportation problem. The multivalued nature of Fuzzy Sets allows handling of uncertainty and vagueness involved in the cost values of each cells in the transportation table. For finding the initial solution of the transportation problem we use the Fuzzy Vogel Approximation Method and for determining the optimality of the obtained solution Fuzzy Modified Distribution Method is used. The fuzzification of the cost of the transportation problem is discussed with the help of a numerical example. Finally, we discuss the computational complexity involved in the problem. To the best of our knowledge, this is the first work on obtaining the solution of the transportation problem using fuzzy trapezoidal numbers.
Solution of System of Linear Equations - A Neuro-Fuzzy Approach
Apr 26, 2013Abstract:Neuro-Fuzzy Modeling has been applied in a wide variety of fields such as Decision Making, Engineering and Management Sciences etc. In particular, applications of this Modeling technique in Decision Making by involving complex Systems of Linear Algebraic Equations have remarkable significance. In this Paper, we present Polak-Ribiere Conjugate Gradient based Neural Network with Fuzzy rules to solve System of Simultaneous Linear Algebraic Equations. This is achieved using Fuzzy Backpropagation Learning Rule. The implementation results show that the proposed Neuro-Fuzzy Network yields effective solutions for exactly determined, underdetermined and over-determined Systems of Linear Equations. This fact is demonstrated by the Computational Complexity analysis of the Neuro-Fuzzy Algorithm. The proposed Algorithm is simulated effectively using MATLAB software. To the best of our knowledge this is the first work of the Systems of Linear Algebraic Equations using Neuro-Fuzzy Modeling.
Solution of the Decision Making Problems using Fuzzy Soft Relations
Apr 26, 2013
Abstract:The Fuzzy Modeling has been applied in a wide variety of fields such as Engineering and Management Sciences and Social Sciences to solve a number Decision Making Problems which involve impreciseness, uncertainty and vagueness in data. In particular, applications of this Modeling technique in Decision Making Problems have remarkable significance. These problems have been tackled using various theories such as Probability theory, Fuzzy Set Theory, Rough Set Theory, Vague Set Theory, Approximate Reasoning Theory etc. which lack in parameterization of the tools due to which they could not be applied successfully to such problems. The concept of Soft Set has a promising potential for giving an optimal solution for these problems. With the motivation of this new concept, in this paper we define the concepts of Soft Relation and Fuzzy Soft Relation and then apply them to solve a number of Decision Making Problems. The advantages of Fuzzy Soft Relation compared to other paradigms are discussed. To the best of our knowledge this is the first work on the application of Fuzzy Soft Relation to the Decision Making Problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge