Smart Traffic Management of Vehicles using Faster R-CNN based Deep Learning Method

With constant growth of civilization and modernization of cities all across the world since past few centuries smart traffic management of vehicles is one of the most sorted after problem by research community. It is a challenging problem in computer vision and artificial intelligence domain. Smart traffic management basically involves segmentation of vehicles, estimation of traffic density and tracking of vehicles. The vehicle segmentation from traffic videos helps realization of niche applications such as monitoring of speed and estimation of traffic. When occlusions, background with clutters and traffic with density variations are present, this problem becomes more intractable in nature. Keeping this motivation in this research work, we investigate Faster R-CNN based deep learning method towards segmentation of vehicles. This problem is addressed in four steps viz minimization with adaptive background model, Faster R-CNN based subnet operation, Faster R-CNN initial refinement and result optimization with extended topological active nets. The computational framework uses ideas of adaptive background modeling. It also addresses shadow and illumination related issues. Higher segmentation accuracy is achieved through topological active net deformable models. The topological and extended topological active nets help to achieve stated deformations. Mesh deformation is achieved with minimization of energy. The segmentation accuracy is improved with modified version of extended topological active net. The experimental results demonstrate superiority of this computational framework

B-Splines

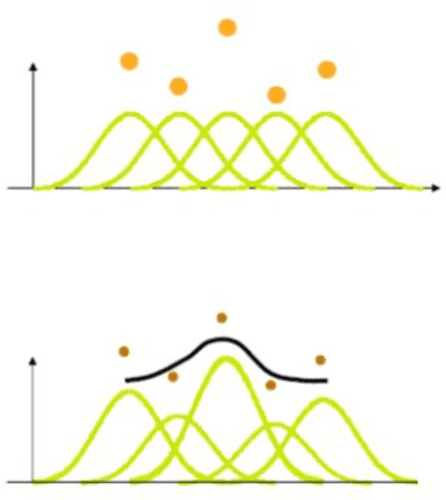
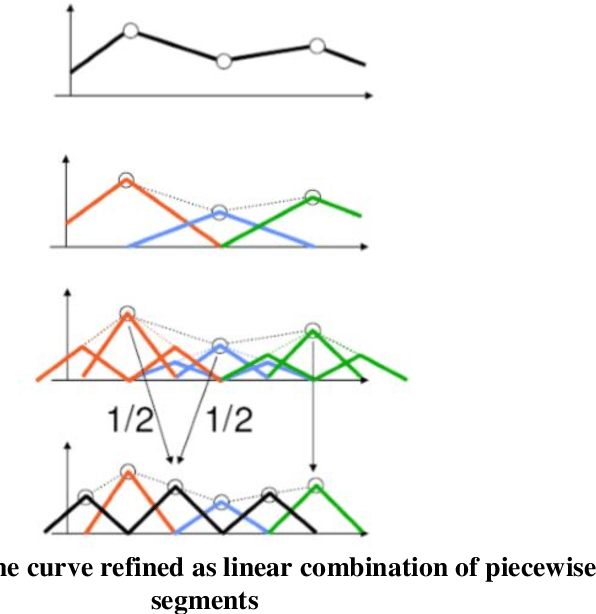
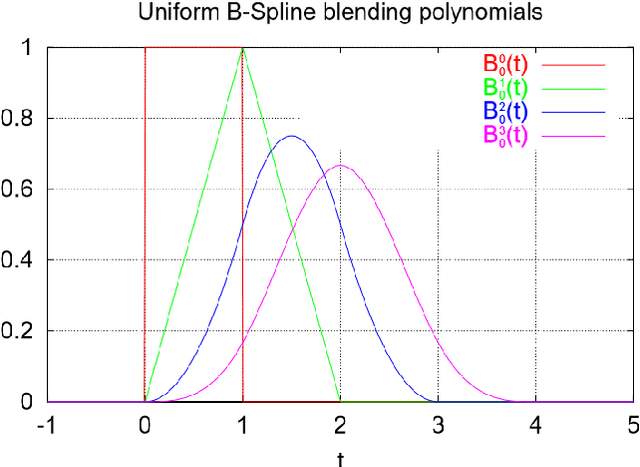
BSplines are one of the most promising curves in computer graphics. They are blessed with some superior geometric properties which make them an ideal candidate for several applications in computer aided design industry. In this article, some basic properties of B-Spline curves are presented. Two significant B-Spline properties viz convex hull property and repeated points effects are discussed. The BSplines computation in computational devices is also illustrated. An industry application based on image processing where B-Spline curve reconstructs the 3D surfaces for CT image datasets of inner organs further highlights the strength of these curves

Detecting Vehicle Type and License Plate Number of different Vehicles on Images

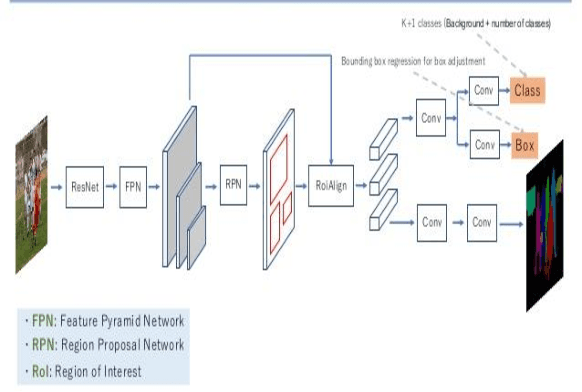
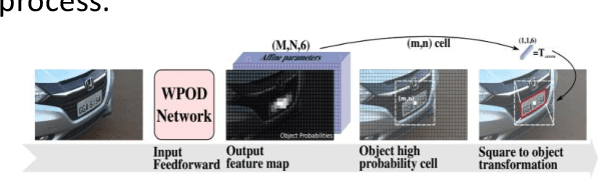
With ever increasing number of vehicles, vehicular tracking is one of the major challenges faced by urban areas. In this paper we try to develop a model that can locate a particular vehicle that the user is looking for depending on two factors 1. the Type of vehicle and the 2. License plate number of the car. The proposed system uses a unique mixture consisting of Mask R-CNN model for vehicle type detection, WpodNet and pytesseract for License Plate detection and Prediction of letters in it.

Predictive Maintenance for Industrial IoT of Vehicle Fleets using Hierarchical Modified Fuzzy Support Vector Machine

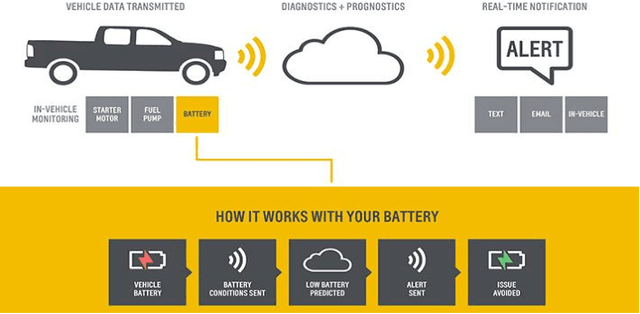
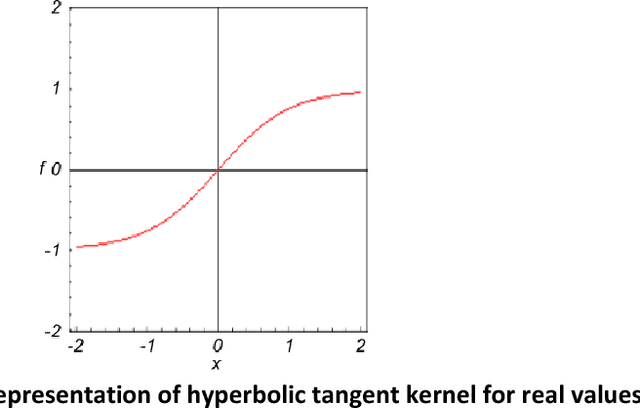
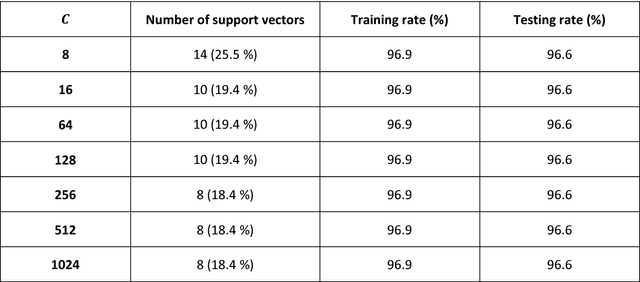
Connected vehicle fleets are deployed worldwide in several industrial IoT scenarios. With the gradual increase of machines being controlled and managed through networked smart devices, the predictive maintenance potential grows rapidly. Predictive maintenance has the potential of optimizing uptime as well as performance such that time and labor associated with inspections and preventive maintenance are reduced. In order to understand the trends of vehicle faults with respect to important vehicle attributes viz mileage, age, vehicle type etc this problem is addressed through hierarchical modified fuzzy support vector machine (HMFSVM). The proposed method is compared with other commonly used approaches like logistic regression, random forests and support vector machines. This helps better implementation of telematics data to ensure preventative management as part of the desired solution. The superiority of the proposed method is highlighted through several experimental results.

An Epsilon Hierarchical Fuzzy Twin Support Vector Regression

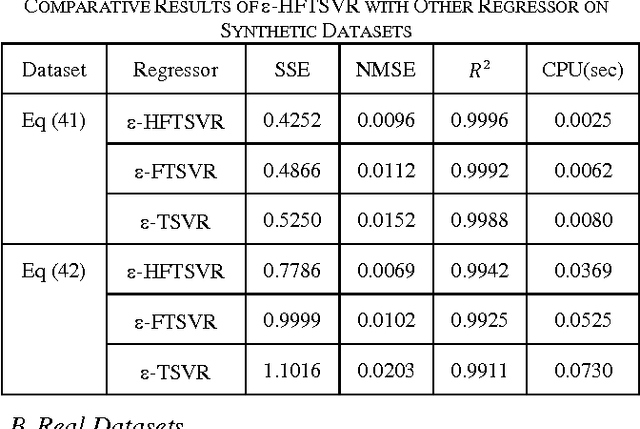
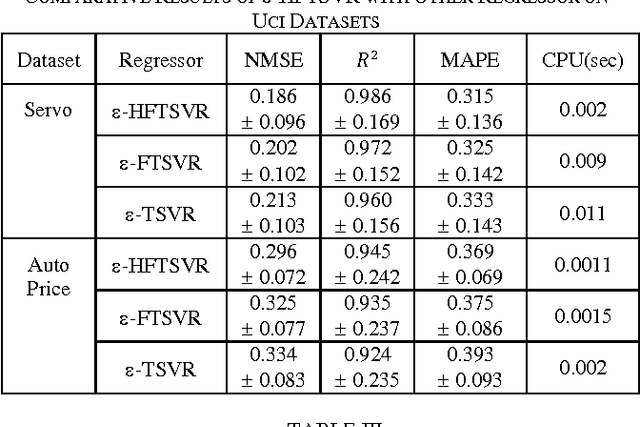
The research presents epsilon hierarchical fuzzy twin support vector regression based on epsilon fuzzy twin support vector regression and epsilon twin support vector regression. Epsilon FTSVR is achieved by incorporating trapezoidal fuzzy numbers to epsilon TSVR which takes care of uncertainty existing in forecasting problems. Epsilon FTSVR determines a pair of epsilon insensitive proximal functions by solving two related quadratic programming problems. The structural risk minimization principle is implemented by introducing regularization term in primal problems of epsilon FTSVR. This yields dual stable positive definite problems which improves regression performance. Epsilon FTSVR is then reformulated as epsilon HFTSVR consisting of a set of hierarchical layers each containing epsilon FTSVR. Experimental results on both synthetic and real datasets reveal that epsilon HFTSVR has remarkable generalization performance with minimum training time.

Fuzzy Mixed Integer Linear Programming for Air Vehicles Operations Optimization

Multiple Air Vehicles (AVs) to prosecute geographically dispersed targets is an important optimization problem. Associated multiple tasks viz., target classification, attack and verification are successively performed on each target. The optimal minimum time performance of these tasks requires cooperation among vehicles such that critical time constraints are satisfied i.e. target must be classified before it can be attacked and AV is sent to target area to verify its destruction after target has been attacked. Here, optimal task scheduling problem from Indian Air Force is formulated as Fuzzy Mixed Integer Linear Programming (FMILP) problem. The solution assigns all tasks to vehicles and performs scheduling in an optimal manner including scheduled staged departure times. Coupled tasks involving time and task order constraints are addressed. When AVs have sufficient endurance, existence of optimal solution is guaranteed. The solution developed can serve as an effective heuristic for different categories of AV optimization problems.

Fuzzy Mixed Integer Optimization Model for Regression Approach

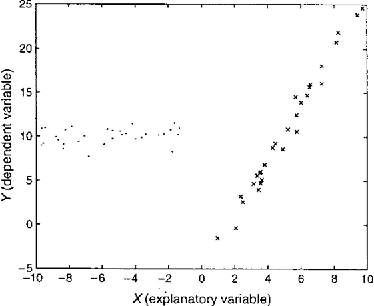
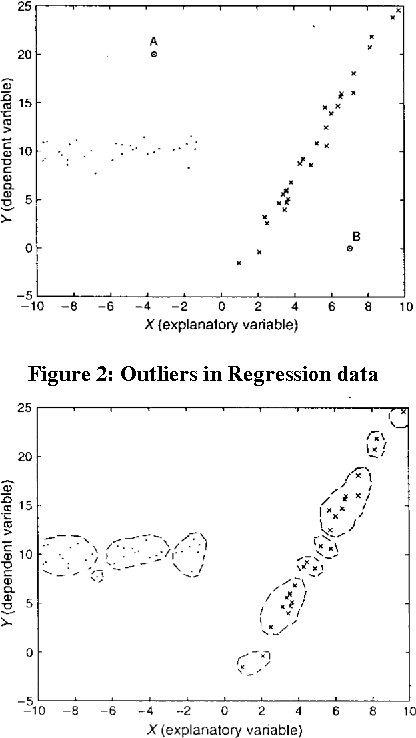
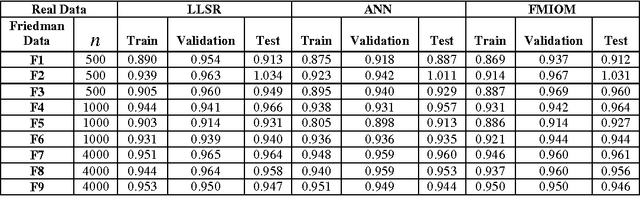
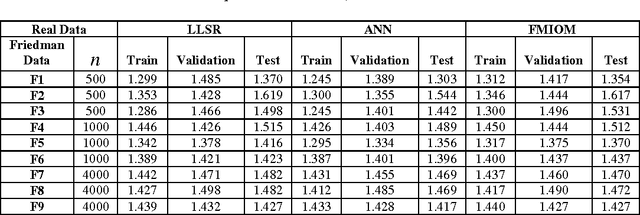
Mixed Integer Optimization has been a topic of active research in past decades. It has been used to solve Statistical problems of classification and regression involving massive data. However, there is an inherent degree of vagueness present in huge real life data. This impreciseness is handled by Fuzzy Sets. In this Paper, Fuzzy Mixed Integer Optimization Method (FMIOM) is used to find solution to Regression problem. The methodology exploits discrete character of problem. In this way large scale problems are solved within practical limits. The data points are separated into different polyhedral regions and each region has its own distinct regression coefficients. In this attempt, an attention is drawn to Statistics and Data Mining community that Integer Optimization can be significantly used to revisit different Statistical problems. Computational experimentations with generated and real data sets show that FMIOM is comparable to and often outperforms current leading methods. The results illustrate potential for significant impact of Fuzzy Integer Optimization methods on Computational Statistics and Data Mining.

Support Vector Machine Model for Currency Crisis Discrimination

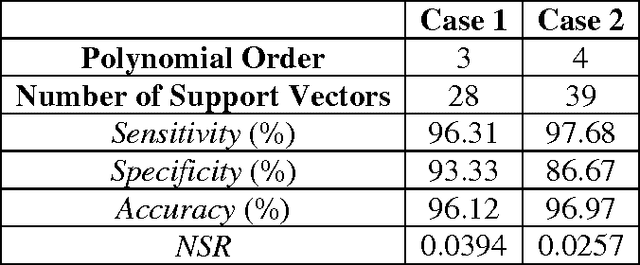
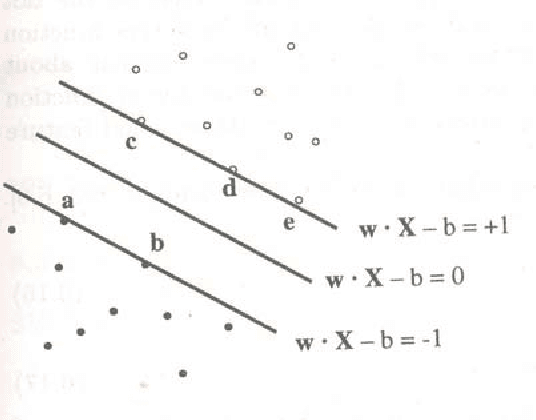
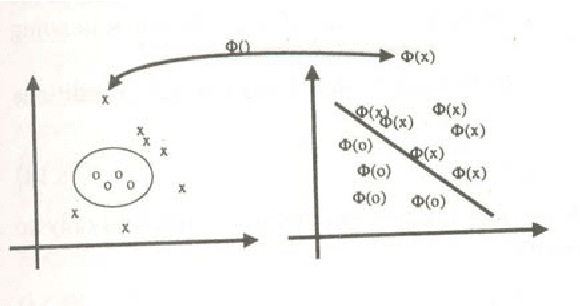
Support Vector Machine (SVM) is powerful classification technique based on the idea of structural risk minimization. Use of kernel function enables curse of dimensionality to be addressed. However, proper kernel function for certain problem is dependent on specific dataset and as such there is no good method on choice of kernel function. In this paper, SVM is used to build empirical models of currency crisis in Argentina. An estimation technique is developed by training model on real life data set which provides reasonably accurate model outputs and helps policy makers to identify situations in which currency crisis may happen. The third and fourth order polynomial kernel is generally best choice to achieve high generalization of classifier performance. SVM has high level of maturity with algorithms that are simple, easy to implement, tolerates curse of dimensionality and good empirical performance. The satisfactory results show that currency crisis situation is properly emulated using only small fraction of database and could be used as an evaluation tool as well as an early warning system. To the best of knowledge this is the first work on SVM approach for currency crisis evaluation of Argentina.

A Dynamic Algorithm for the Longest Common Subsequence Problem using Ant Colony Optimization Technique

We present a dynamic algorithm for solving the Longest Common Subsequence Problem using Ant Colony Optimization Technique. The Ant Colony Optimization Technique has been applied to solve many problems in Optimization Theory, Machine Learning and Telecommunication Networks etc. In particular, application of this theory in NP-Hard Problems has a remarkable significance. Given two strings, the traditional technique for finding Longest Common Subsequence is based on Dynamic Programming which consists of creating a recurrence relation and filling a table of size . The proposed algorithm draws analogy with behavior of ant colonies function and this new computational paradigm is known as Ant System. It is a viable new approach to Stochastic Combinatorial Optimization. The main characteristics of this model are positive feedback, distributed computation, and the use of constructive greedy heuristic. Positive feedback accounts for rapid discovery of good solutions, distributed computation avoids premature convergence and greedy heuristic helps find acceptable solutions in minimum number of stages. We apply the proposed methodology to Longest Common Subsequence Problem and give the simulation results. The effectiveness of this approach is demonstrated by efficient Computational Complexity. To the best of our knowledge, this is the first Ant Colony Optimization Algorithm for Longest Common Subsequence Problem.

Achieving greater Explanatory Power and Forecasting Accuracy with Non-uniform spread Fuzzy Linear Regression

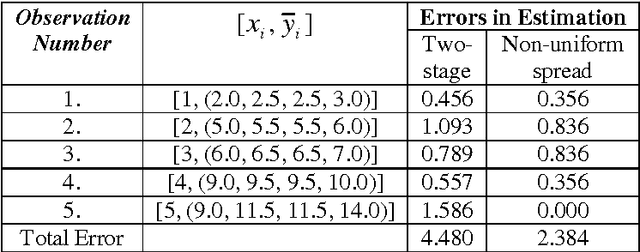
Fuzzy regression models have been applied to several Operations Research applications viz., forecasting and prediction. Earlier works on fuzzy regression analysis obtain crisp regression coefficients for eliminating the problem of increasing spreads for the estimated fuzzy responses as the magnitude of the independent variable increases. But they cannot deal with the problem of non-uniform spreads. In this work, a three-phase approach is discussed to construct the fuzzy regression model with non-uniform spreads to deal with this problem. The first phase constructs the membership functions of the least-squares estimates of regression coefficients based on extension principle to completely conserve the fuzziness of observations. They are then defuzzified by the centre of area method to obtain crisp regression coefficients in the second phase. Finally, the error terms of the method are determined by setting each estimated spread equal to its corresponding observed spread. The Tagaki-Sugeno inference system is used for improving the accuracy of forecasts. The simulation example demonstrates the strength of fuzzy linear regression model in terms of higher explanatory power and forecasting performance.