Algorithm Unrolling-based Denoising of Multimodal Graph Signals

We propose a denoising method of multimodal graph signals by iteratively solving signal restoration and graph learning problems. Many complex-structured data, i.e., those on sensor networks, can capture multiple modalities at each measurement point, referred to as modalities. They are also assumed to have an underlying structure or correlations in modality as well as space. Such multimodal data are regarded as graph signals on a twofold graph and they are often corrupted by noise. Furthermore, their spatial/modality relationships are not always given a priori: We need to estimate twofold graphs during a denoising algorithm. In this paper, we consider a signal denoising method on twofold graphs, where graphs are learned simultaneously. We formulate an optimization problem for that and parameters in an iterative algorithm are learned from training data by unrolling the iteration with deep algorithm unrolling. Experimental results on synthetic and real-world data demonstrate that the proposed method outperforms existing model- and deep learning-based graph signal denoising methods.

Joint Graph Estimation and Signal Restoration for Robust Federated Learning

We propose a robust aggregation method for model parameters in federated learning (FL) under noisy communications. FL is a distributed machine learning paradigm in which a central server aggregates local model parameters from multiple clients. These parameters are often noisy and/or have missing values during data collection, training, and communication between the clients and server. This may cause a considerable drop in model accuracy. To address this issue, we learn a graph that represents pairwise relationships between model parameters of the clients during aggregation. We realize it with a joint problem of graph learning and signal (i.e., model parameters) restoration. The problem is formulated as a difference-of-convex (DC) optimization, which is efficiently solved via a proximal DC algorithm. Experimental results on MNIST and CIFAR-10 datasets show that the proposed method outperforms existing approaches by up to $2$--$5\%$ in classification accuracy under biased data distributions and noisy conditions.

Multiscale Graph Construction Using Non-local Cluster Features

This paper presents a multiscale graph construction method using both graph and signal features. Multiscale graph is a hierarchical representation of the graph, where a node at each level indicates a cluster in a finer resolution. To obtain the hierarchical clusters, existing methods often use graph clustering; however, they may ignore signal variations. As a result, these methods could fail to detect the clusters having similar features on nodes. In this paper, we consider graph and node-wise features simultaneously for multiscale clustering of a graph. With given clusters of the graph, the clusters are merged hierarchically in three steps: 1) Feature vectors in the clusters are extracted. 2) Similarities among cluster features are calculated using optimal transport. 3) A variable $k$-nearest neighbor graph (V$k$NNG) is constructed and graph spectral clustering is applied to the V$k$NNG to obtain clusters at a coarser scale. Additionally, the multiscale graph in this paper has \textit{non-local} characteristics: Nodes with similar features are merged even if they are spatially separated. In experiments on multiscale image and point cloud segmentation, we demonstrate the effectiveness of the proposed method.

Time-Varying Graph Signal Estimation among Multiple Sub-Networks

This paper presents an estimation method for time-varying graph signals among multiple sub-networks. In many sensor networks, signals observed are associated with nodes (i.e., sensors), and edges of the network represent the inter-node connectivity. For a large sensor network, measuring signal values at all nodes over time requires huge resources, particularly in terms of energy consumption. To alleviate the issue, we consider a scenario that a sub-network, i.e., cluster, from the whole network is extracted and an intra-cluster analysis is performed based on the statistics in the cluster. The statistics are then utilized to estimate signal values in another cluster. This leads to the requirement for transferring a set of parameters of the sub-network to the others, while the numbers of nodes in the clusters are typically different. In this paper, we propose a cooperative Kalman filter between two sub-networks. The proposed method alternately estimates signals in time between two sub-networks. We formulate a state-space model in the source cluster and transfer it to the target cluster on the basis of optimal transport. In the signal estimation experiments of synthetic and real-world signals, we validate the effectiveness of the proposed method.

Lossy Compression of Adjacency Matrices by Graph Filter Banks

This paper proposes a compression framework for adjacency matrices of weighted graphs based on graph filter banks. Adjacency matrices are widely used mathematical representations of graphs and are used in various applications in signal processing, machine learning, and data mining. In many problems of interest, these adjacency matrices can be large, so efficient compression methods are crucial. In this paper, we propose a lossy compression of weighted adjacency matrices, where the binary adjacency information is encoded losslessly (so the topological information of the graph is preserved) while the edge weights are compressed lossily. For the edge weight compression, the target graph is converted into a line graph, whose nodes correspond to the edges of the original graph, and where the original edge weights are regarded as a graph signal on the line graph. We then transform the edge weights on the line graph with a graph filter bank for sparse representation. Experiments on synthetic data validate the effectiveness of the proposed method by comparing it with existing lossy matrix compression methods.

Optimizing $k$ in $k$NN Graphs with Graph Learning Perspective

In this paper, we propose a method, based on graph signal processing, to optimize the choice of $k$ in $k$-nearest neighbor graphs ($k$NNGs). $k$NN is one of the most popular approaches and is widely used in machine learning and signal processing. The parameter $k$ represents the number of neighbors that are connected to the target node; however, its appropriate selection is still a challenging problem. Therefore, most $k$NNGs use ad hoc selection methods for $k$. In the proposed method, we assume that a different $k$ can be chosen for each node. We formulate a discrete optimization problem to seek the best $k$ with a constraint on the sum of distances of the connected nodes. The optimal $k$ values are efficiently obtained without solving a complex optimization. Furthermore, we reveal that the proposed method is closely related to existing graph learning methods. In experiments on real datasets, we demonstrate that the $k$NNGs obtained with our method are sparse and can determine an appropriate variable number of edges per node. We validate the effectiveness of the proposed method for point cloud denoising, comparing our denoising performance with achievable graph construction methods that can be scaled to typical point cloud sizes (e.g., thousands of nodes).

Dynamic Sensor Placement Based on Graph Sampling Theory

In this paper, we consider a dynamic sensor placement problem where sensors can move within a network over time. Sensor placement problem aims to select M sensor positions from N candidates where M < N. Most existing methods assume that sensors are static, i.e., they do not move, however, many mobile sensors like drones, robots, and vehicles can change their positions over time. Moreover, underlying measurement conditions could also be changed that are difficult to cover the statically placed sensors. We tackle the problem by allowing the sensors to change their positions in their neighbors on the network. Based on a perspective of dictionary learning, we sequentially learn the dictionary from a pool of observed signals on the network based on graph sampling theory. Using the learned dictionary, we dynamically determine the sensor positions such that the non-observed signals on the network can be best recovered from the observations. Furthermore, sensor positions in each time slot can be optimized in a decentralized manner to reduce the calculation cost. In experiments, we validate the effectiveness of the proposed method via the mean squared error (MSE) of the reconstructed signals. The proposed dynamic sensor placement outperforms the existing static ones both in synthetic and real data.

Multi-channel Sampling on Graphs and Its Relationship to Graph Filter Banks

In this paper, we consider multi-channel sampling (MCS) for graph signals. We generally encounter full-band graph signals beyond the bandlimited one in many applications, such as piecewise constant/smooth and union of bandlimited graph signals. Full-band graph signals can be represented by a mixture of multiple signals conforming to different generation models. This requires the analysis of graph signals via multiple sampling systems, i.e., MCS, while existing approaches only consider single-channel sampling. We develop a MCS framework based on generalized sampling. We also present a sampling set selection (SSS) method for the proposed MCS so that the graph signal is best recovered. Furthermore, we reveal that existing graph filter banks can be viewed as a special case of the proposed MCS. In signal recovery experiments, the proposed method exhibits the effectiveness of recovery for full-band graph signals.

Graph Signal Sampling Under Stochastic Priors

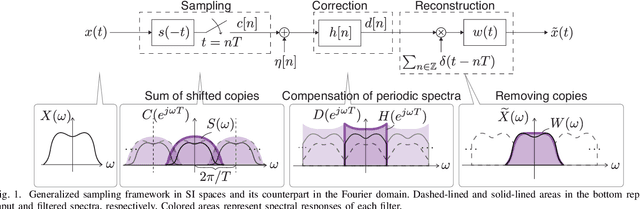
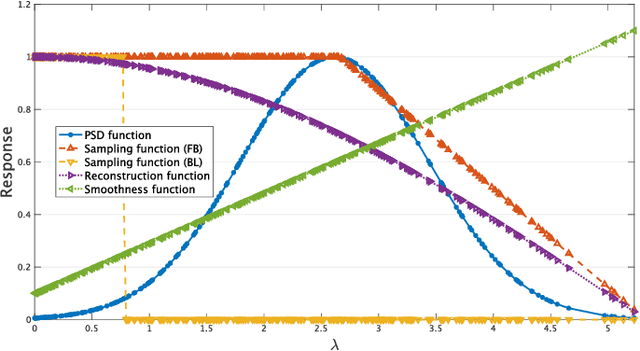
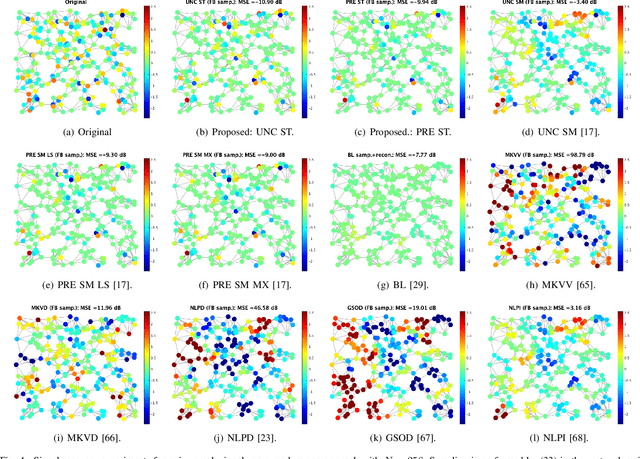
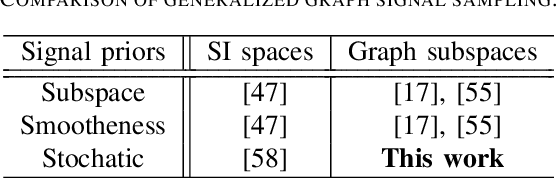
We propose a generalized sampling framework for stochastic graph signals. Stochastic graph signals are characterized by graph wide sense stationarity (GWSS) which is an extension of wide sense stationarity (WSS) for standard time-domain signals. In this paper, graph signals are assumed to satisfy the GWSS conditions and we study their sampling as well as recovery procedures. In generalized sampling, a correction filter is inserted between sampling and reconstruction operators to compensate for non-ideal measurements. We propose a design method for the correction filters to reduce the mean-squared error (MSE) between original and reconstructed graph signals. We derive the correction filters for two cases: The reconstruction filter is arbitrarily chosen or predefined. The proposed framework allows for arbitrary sampling methods, i.e., sampling in the vertex or graph frequency domain. We also show that the graph spectral response of the resulting correction filter parallels that for generalized sampling for WSS signals if sampling is performed in the graph frequency domain. The effectiveness of our approach is validated via experiments by comparing its MSE with existing approaches.