A New Convergence Analysis of Plug-and-Play Proximal Gradient Descent Under Prior Mismatch

In this work, we provide a new convergence theory for plug-and-play proximal gradient descent (PnP-PGD) under prior mismatch where the denoiser is trained on a different data distribution to the inference task at hand. To the best of our knowledge, this is the first convergence proof of PnP-PGD under prior mismatch. Compared with the existing theoretical results for PnP algorithms, our new results removed the need for several restrictive and unverifiable assumptions.

The Practicality of Normalizing Flow Test-Time Training in Bayesian Inference for Agent-Based Models

Agent-Based Models (ABMs) are gaining great popularity in economics and social science because of their strong flexibility to describe the realistic and heterogeneous decisions and interaction rules between individual agents. In this work, we investigate for the first time the practicality of test-time training (TTT) of deep models such as normalizing flows, in the parameters posterior estimations of ABMs. We propose several practical TTT strategies for fine-tuning the normalizing flow against distribution shifts. Our numerical study demonstrates that TTT schemes are remarkably effective, enabling real-time adjustment of flow-based inference for ABM parameters.

From Image Denoisers to Regularizing Imaging Inverse Problems: An Overview

Inverse problems lie at the heart of modern imaging science, with broad applications in areas such as medical imaging, remote sensing, and microscopy. Recent years have witnessed a paradigm shift in solving imaging inverse problems, where data-driven regularizers are used increasingly, leading to remarkably high-fidelity reconstruction. A particularly notable approach for data-driven regularization is to use learned image denoisers as implicit priors in iterative image reconstruction algorithms. This survey presents a comprehensive overview of this powerful and emerging class of algorithms, commonly referred to as plug-and-play (PnP) methods. We begin by providing a brief background on image denoising and inverse problems, followed by a short review of traditional regularization strategies. We then explore how proximal splitting algorithms, such as the alternating direction method of multipliers (ADMM) and proximal gradient descent (PGD), can naturally accommodate learned denoisers in place of proximal operators, and under what conditions such replacements preserve convergence. The role of Tweedie's formula in connecting optimal Gaussian denoisers and score estimation is discussed, which lays the foundation for regularization-by-denoising (RED) and more recent diffusion-based posterior sampling methods. We discuss theoretical advances regarding the convergence of PnP algorithms, both within the RED and proximal settings, emphasizing the structural assumptions that the denoiser must satisfy for convergence, such as non-expansiveness, Lipschitz continuity, and local homogeneity. We also address practical considerations in algorithm design, including choices of denoiser architecture and acceleration strategies.

Fast Equivariant Imaging: Acceleration for Unsupervised Learning via Augmented Lagrangian and Auxiliary PnP Denoisers

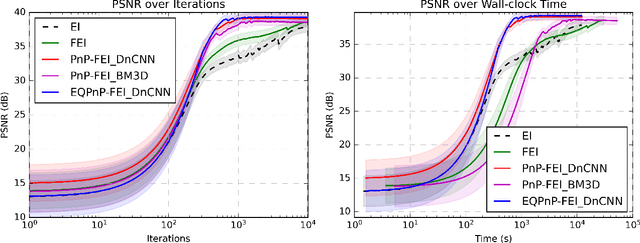
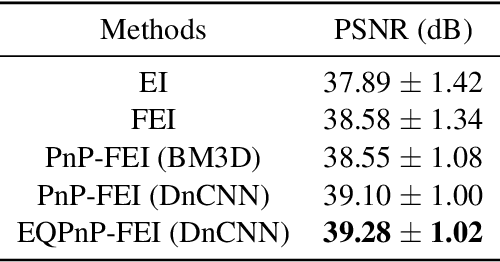
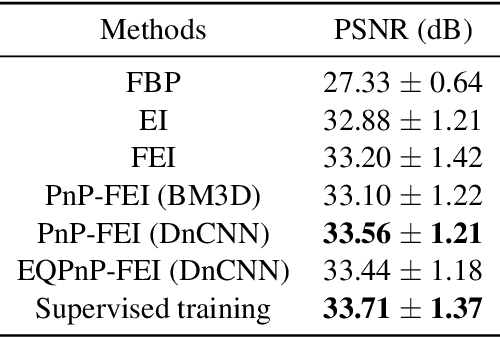
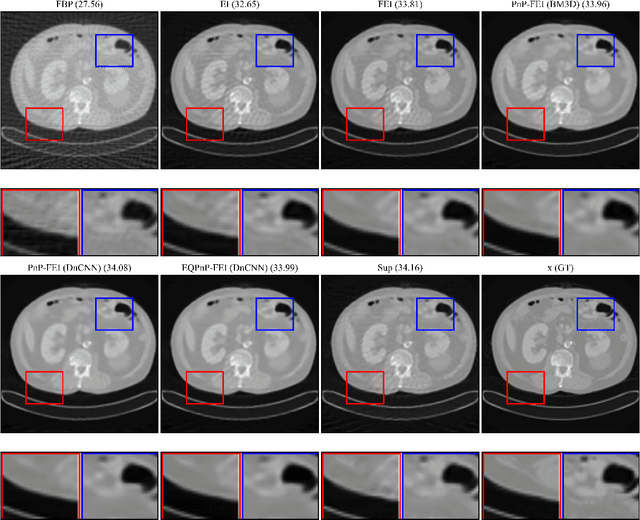
We propose Fast Equivariant Imaging (FEI), a novel unsupervised learning framework to efficiently train deep imaging networks without ground-truth data. From the perspective of reformulating the Equivariant Imaging based optimization problem via the method of Lagrange multipliers and utilizing plug-and-play denoisers, this novel unsupervised scheme shows superior efficiency and performance compared to vanilla Equivariant Imaging paradigm. In particular, our PnP-FEI scheme achieves an order-of-magnitude (10x) acceleration over standard EI on training U-Net with CT100 dataset for X-ray CT reconstruction, with improved generalization performance.

Sketched Equivariant Imaging Regularization and Deep Internal Learning for Inverse Problems

Equivariant Imaging (EI) regularization has become the de-facto technique for unsupervised training of deep imaging networks, without any need of ground-truth data. Observing that the EI-based unsupervised training paradigm currently has significant computational redundancy leading to inefficiency in high-dimensional applications, we propose a sketched EI regularization which leverages the randomized sketching techniques for acceleration. We then extend our sketched EI regularization to develop an accelerated deep internal learning framework -- Sketched Equivariant Deep Image Prior (Sk.EI-DIP), which can be efficiently applied for single-image and task-adapted reconstruction. Our numerical study on X-ray CT image reconstruction tasks demonstrate that our approach can achieve order-of-magnitude computational acceleration over standard EI-based counterpart in single-input setting, and network adaptation at test time.

Blessing of Dimensionality for Approximating Sobolev Classes on Manifolds

The manifold hypothesis says that natural high-dimensional data is actually supported on or around a low-dimensional manifold. Recent success of statistical and learning-based methods empirically supports this hypothesis, due to outperforming classical statistical intuition in very high dimensions. A natural step for analysis is thus to assume the manifold hypothesis and derive bounds that are independent of any embedding space. Theoretical implications in this direction have recently been explored in terms of generalization of ReLU networks and convergence of Langevin methods. We complement existing results by providing theoretical statistical complexity results, which directly relates to generalization properties. In particular, we demonstrate that the statistical complexity required to approximate a class of bounded Sobolev functions on a compact manifold is bounded from below, and moreover that this bound is dependent only on the intrinsic properties of the manifold. These provide complementary bounds for existing approximation results for ReLU networks on manifolds, which give upper bounds on generalization capacity.

A Guide to Stochastic Optimisation for Large-Scale Inverse Problems

Stochastic optimisation algorithms are the de facto standard for machine learning with large amounts of data. Handling only a subset of available data in each optimisation step dramatically reduces the per-iteration computational costs, while still ensuring significant progress towards the solution. Driven by the need to solve large-scale optimisation problems as efficiently as possible, the last decade has witnessed an explosion of research in this area. Leveraging the parallels between machine learning and inverse problems has allowed harnessing the power of this research wave for solving inverse problems. In this survey, we provide a comprehensive account of the state-of-the-art in stochastic optimisation from the viewpoint of inverse problems. We present algorithms with diverse modalities of problem randomisation and discuss the roles of variance reduction, acceleration, higher-order methods, and other algorithmic modifications, and compare theoretical results with practical behaviour. We focus on the potential and the challenges for stochastic optimisation that are unique to inverse imaging problems and are not commonly encountered in machine learning. We conclude the survey with illustrative examples from imaging problems to examine the advantages and disadvantages that this new generation of algorithms bring to the field of inverse problems.

Unsupervised Training of Convex Regularizers using Maximum Likelihood Estimation

Unsupervised learning is a training approach in the situation where ground truth data is unavailable, such as inverse imaging problems. We present an unsupervised Bayesian training approach to learning convex neural network regularizers using a fixed noisy dataset, based on a dual Markov chain estimation method. Compared to classical supervised adversarial regularization methods, where there is access to both clean images as well as unlimited to noisy copies, we demonstrate close performance on natural image Gaussian deconvolution and Poisson denoising tasks.

Unsupervised approaches based on optimal transport and convex analysis for inverse problems in imaging

Unsupervised deep learning approaches have recently become one of the crucial research areas in imaging owing to their ability to learn expressive and powerful reconstruction operators even when paired high-quality training data is scarcely available. In this chapter, we review theoretically principled unsupervised learning schemes for solving imaging inverse problems, with a particular focus on methods rooted in optimal transport and convex analysis. We begin by reviewing the optimal transport-based unsupervised approaches such as the cycle-consistency-based models and learned adversarial regularization methods, which have clear probabilistic interpretations. Subsequently, we give an overview of a recent line of works on provably convergent learned optimization algorithms applied to accelerate the solution of imaging inverse problems, alongside their dedicated unsupervised training schemes. We also survey a number of provably convergent plug-and-play algorithms (based on gradient-step deep denoisers), which are among the most important and widely applied unsupervised approaches for imaging problems. At the end of this survey, we provide an overview of a few related unsupervised learning frameworks that complement our focused schemes. Together with a detailed survey, we provide an overview of the key mathematical results that underlie the methods reviewed in the chapter to keep our discussion self-contained.

Deep Unrolling Networks with Recurrent Momentum Acceleration for Nonlinear Inverse Problems

Combining the strengths of model-based iterative algorithms and data-driven deep learning solutions, deep unrolling networks (DuNets) have become a popular tool to solve inverse imaging problems. While DuNets have been successfully applied to many linear inverse problems, nonlinear problems tend to impair the performance of the method. Inspired by momentum acceleration techniques that are often used in optimization algorithms, we propose a recurrent momentum acceleration (RMA) framework that uses a long short-term memory recurrent neural network (LSTM-RNN) to simulate the momentum acceleration process. The RMA module leverages the ability of the LSTM-RNN to learn and retain knowledge from the previous gradients. We apply RMA to two popular DuNets -- the learned proximal gradient descent (LPGD) and the learned primal-dual (LPD) methods, resulting in LPGD-RMA and LPD-RMA respectively. We provide experimental results on two nonlinear inverse problems: a nonlinear deconvolution problem, and an electrical impedance tomography problem with limited boundary measurements. In the first experiment we have observed that the improvement due to RMA largely increases with respect to the nonlinearity of the problem. The results of the second example further demonstrate that the RMA schemes can significantly improve the performance of DuNets in strongly ill-posed problems.