Online Detecting LLM-Generated Texts via Sequential Hypothesis Testing by Betting

Developing algorithms to differentiate between machine-generated texts and human-written texts has garnered substantial attention in recent years. Existing methods in this direction typically concern an offline setting where a dataset containing a mix of real and machine-generated texts is given upfront, and the task is to determine whether each sample in the dataset is from a large language model (LLM) or a human. However, in many practical scenarios, sources such as news websites, social media accounts, or on other forums publish content in a streaming fashion. Therefore, in this online scenario, how to quickly and accurately determine whether the source is an LLM with strong statistical guarantees is crucial for these media or platforms to function effectively and prevent the spread of misinformation and other potential misuse of LLMs. To tackle the problem of online detection, we develop an algorithm based on the techniques of sequential hypothesis testing by betting that not only builds upon and complements existing offline detection techniques but also enjoys statistical guarantees, which include a controlled false positive rate and the expected time to correctly identify a source as an LLM. Experiments were conducted to demonstrate the effectiveness of our method.

Continuized Acceleration for Quasar Convex Functions in Non-Convex Optimization

Quasar convexity is a condition that allows some first-order methods to efficiently minimize a function even when the optimization landscape is non-convex. Previous works develop near-optimal accelerated algorithms for minimizing this class of functions, however, they require a subroutine of binary search which results in multiple calls to gradient evaluations in each iteration, and consequently the total number of gradient evaluations does not match a known lower bound. In this work, we show that a recently proposed continuized Nesterov acceleration can be applied to minimizing quasar convex functions and achieves the optimal bound with a high probability. Furthermore, we find that the objective functions of training generalized linear models (GLMs) satisfy quasar convexity, which broadens the applicability of the relevant algorithms, while known practical examples of quasar convexity in non-convex learning are sparse in the literature. We also show that if a smooth and one-point strongly convex, Polyak-Lojasiewicz, or quadratic-growth function satisfies quasar convexity, then attaining an accelerated linear rate for minimizing the function is possible under certain conditions, while acceleration is not known in general for these classes of functions.

Towards Understanding GD with Hard and Conjugate Pseudo-labels for Test-Time Adaptation

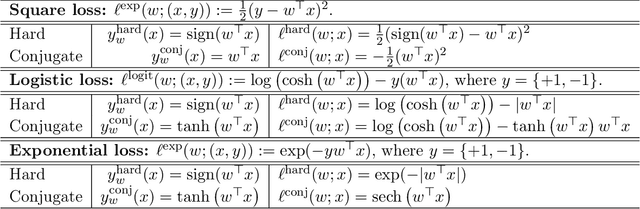
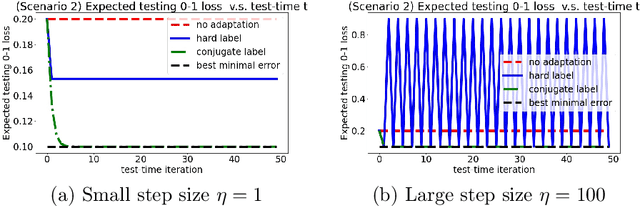
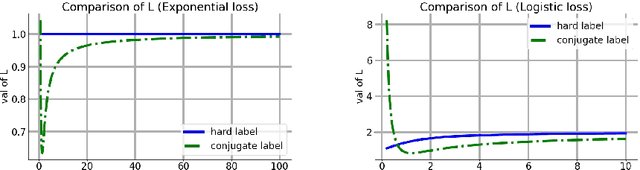
We consider a setting that a model needs to adapt to a new domain under distribution shifts, given that only unlabeled test samples from the new domain are accessible at test time. A common idea in most of the related works is constructing pseudo-labels for the unlabeled test samples and applying gradient descent (GD) to a loss function with the pseudo-labels. Recently, Goyal et al. (2022) propose conjugate labels, which is a new kind of pseudo-labels for self-training at test time. They empirically show that the conjugate label outperforms other ways of pseudo-labeling on many domain adaptation benchmarks. However, provably showing that GD with conjugate labels learns a good classifier for test-time adaptation remains open. In this work, we aim at theoretically understanding GD with hard and conjugate labels for a binary classification problem. We show that for square loss, GD with conjugate labels converges to a solution that minimizes the testing 0-1 loss under a Gaussian model, while GD with hard pseudo-labels fails in this task. We also analyze them under different loss functions for the update. Our results shed lights on understanding when and why GD with hard labels or conjugate labels works in test-time adaptation.

Accelerating Hamiltonian Monte Carlo via Chebyshev Integration Time

Hamiltonian Monte Carlo (HMC) is a popular method in sampling. While there are quite a few works of studying this method on various aspects, an interesting question is how to choose its integration time to achieve acceleration. In this work, we consider accelerating the process of sampling from a distribution $\pi(x) \propto \exp(-f(x))$ via HMC via time-varying integration time. When the potential $f$ is $L$-smooth and $m$-strongly convex, i.e.\ for sampling from a log-smooth and strongly log-concave target distribution $\pi$, it is known that under a constant integration time, the number of iterations that ideal HMC takes to get an $\epsilon$ Wasserstein-2 distance to the target $\pi$ is $O( \kappa \log \frac{1}{\epsilon} )$, where $\kappa := \frac{L}{m}$ is the condition number. We propose a scheme of time-varying integration time based on the roots of Chebyshev polynomials. We show that in the case of quadratic potential $f$, i.e., when the target $\pi$ is a Gaussian distribution, ideal HMC with this choice of integration time only takes $O( \sqrt{\kappa} \log \frac{1}{\epsilon} )$ number of iterations to reach Wasserstein-2 distance less than $\epsilon$; this improvement on the dependence on condition number is akin to acceleration in optimization. The design and analysis of HMC with the proposed integration time is built on the tools of Chebyshev polynomials. Experiments find the advantage of adopting our scheme of time-varying integration time even for sampling from distributions with smooth strongly convex potentials that are not quadratic.

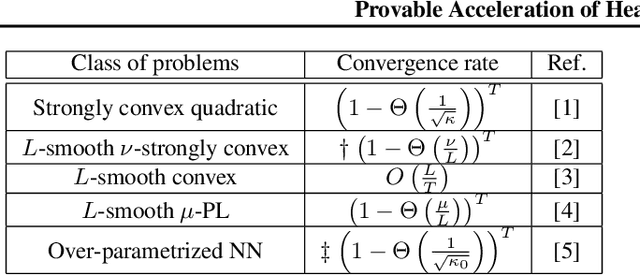
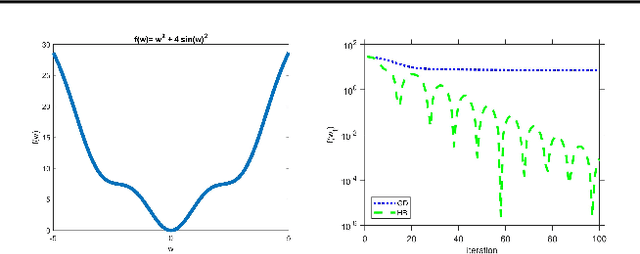
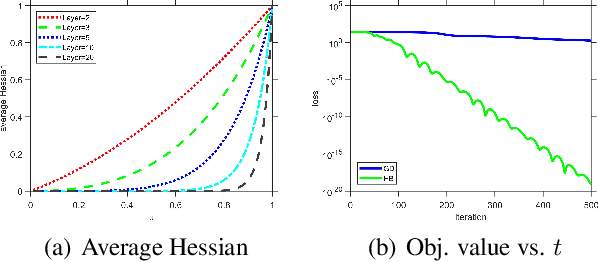
Provable Acceleration of Heavy Ball beyond Quadratics for a Class of Polyak-Łojasiewicz Functions when the Non-Convexity is Averaged-Out

Heavy Ball (HB) nowadays is one of the most popular momentum methods in non-convex optimization. It has been widely observed that incorporating the Heavy Ball dynamic in gradient-based methods accelerates the training process of modern machine learning models. However, the progress on establishing its theoretical foundation of acceleration is apparently far behind its empirical success. Existing provable acceleration results are of the quadratic or close-to-quadratic functions, as the current techniques of showing HB's acceleration are limited to the case when the Hessian is fixed. In this work, we develop some new techniques that help show acceleration beyond quadratics, which is achieved by analyzing how the change of the Hessian at two consecutive time points affects the convergence speed. Based on our technical results, a class of Polyak-\L{}ojasiewicz (PL) optimization problems for which provable acceleration can be achieved via HB is identified. Moreover, our analysis demonstrates a benefit of adaptively setting the momentum parameter.

No-Regret Dynamics in the Fenchel Game: A Unified Framework for Algorithmic Convex Optimization

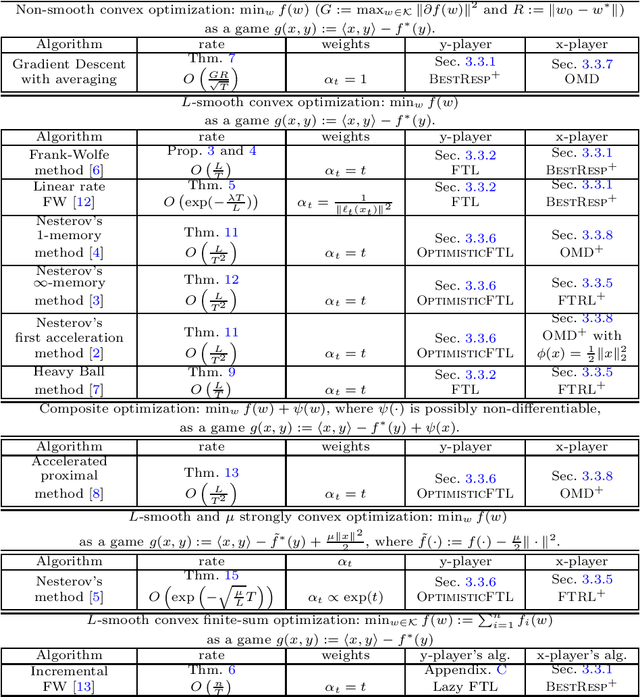
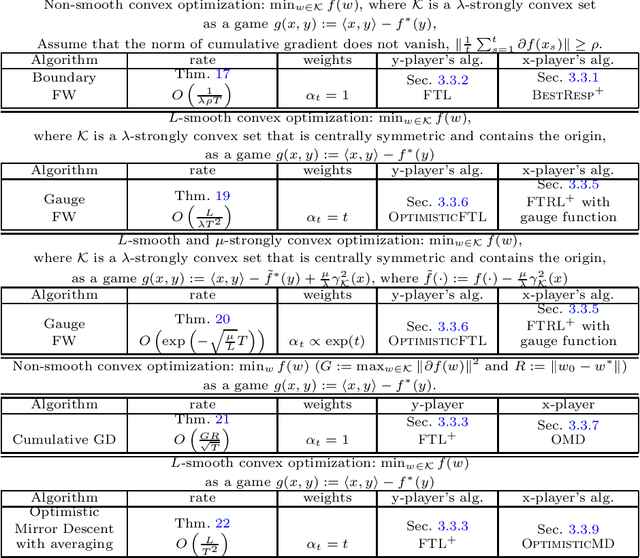
We develop an algorithmic framework for solving convex optimization problems using no-regret game dynamics. By converting the problem of minimizing a convex function into an auxiliary problem of solving a min-max game in a sequential fashion, we can consider a range of strategies for each of the two-players who must select their actions one after the other. A common choice for these strategies are so-called no-regret learning algorithms, and we describe a number of such and prove bounds on their regret. We then show that many classical first-order methods for convex optimization -- including average-iterate gradient descent, the Frank-Wolfe algorithm, the Heavy Ball algorithm, and Nesterov's acceleration methods -- can be interpreted as special cases of our framework as long as each player makes the correct choice of no-regret strategy. Proving convergence rates in this framework becomes very straightforward, as they follow from plugging in the appropriate known regret bounds. Our framework also gives rise to a number of new first-order methods for special cases of convex optimization that were not previously known.

Understanding Modern Techniques in Optimization: Frank-Wolfe, Nesterov's Momentum, and Polyak's Momentum

In the first part of this dissertation research, we develop a modular framework that can serve as a recipe for constructing and analyzing iterative algorithms for convex optimization. Specifically, our work casts optimization as iteratively playing a two-player zero-sum game. Many existing optimization algorithms including Frank-Wolfe and Nesterov's acceleration methods can be recovered from the game by pitting two online learners with appropriate strategies against each other. Furthermore, the sum of the weighted average regrets of the players in the game implies the convergence rate. As a result, our approach provides simple alternative proofs to these algorithms. Moreover, we demonstrate that our approach of optimization as iteratively playing a game leads to three new fast Frank-Wolfe-like algorithms for some constraint sets, which further shows that our framework is indeed generic, modular, and easy-to-use. In the second part, we develop a modular analysis of provable acceleration via Polyak's momentum for certain problems, which include solving the classical strongly quadratic convex problems, training a wide ReLU network under the neural tangent kernel regime, and training a deep linear network with an orthogonal initialization. We develop a meta theorem and show that when applying Polyak's momentum for these problems, the induced dynamics exhibit a form where we can directly apply our meta theorem. In the last part of the dissertation, we show another advantage of the use of Polyak's momentum -- it facilitates fast saddle point escape in smooth non-convex optimization. This result, together with those of the second part, sheds new light on Polyak's momentum in modern non-convex optimization and deep learning.

Escaping Saddle Points Faster with Stochastic Momentum

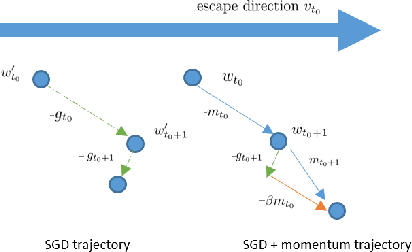
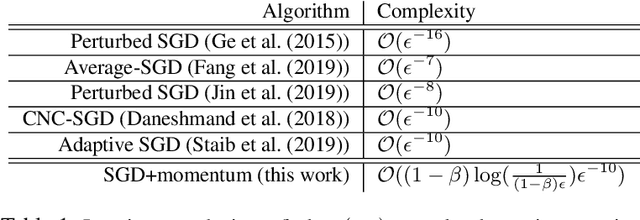
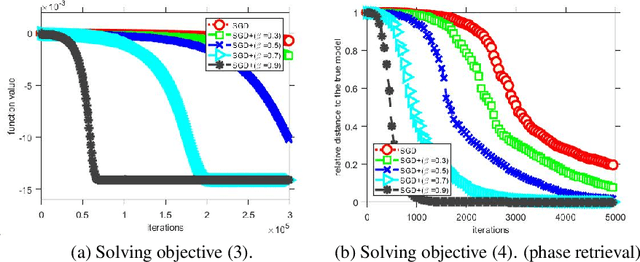
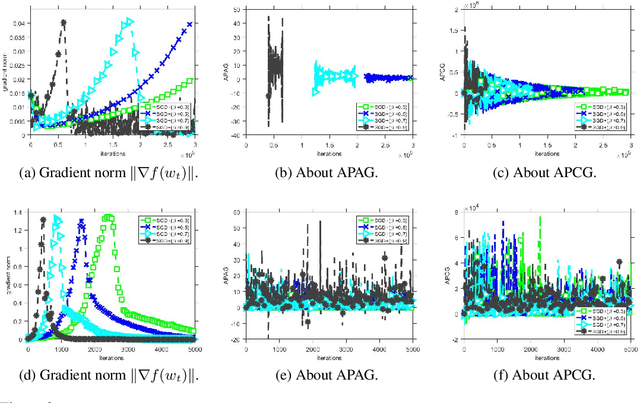
Stochastic gradient descent (SGD) with stochastic momentum is popular in nonconvex stochastic optimization and particularly for the training of deep neural networks. In standard SGD, parameters are updated by improving along the path of the gradient at the current iterate on a batch of examples, where the addition of a ``momentum'' term biases the update in the direction of the previous change in parameters. In non-stochastic convex optimization one can show that a momentum adjustment provably reduces convergence time in many settings, yet such results have been elusive in the stochastic and non-convex settings. At the same time, a widely-observed empirical phenomenon is that in training deep networks stochastic momentum appears to significantly improve convergence time, variants of it have flourished in the development of other popular update methods, e.g. ADAM [KB15], AMSGrad [RKK18], etc. Yet theoretical justification for the use of stochastic momentum has remained a significant open question. In this paper we propose an answer: stochastic momentum improves deep network training because it modifies SGD to escape saddle points faster and, consequently, to more quickly find a second order stationary point. Our theoretical results also shed light on the related question of how to choose the ideal momentum parameter--our analysis suggests that $\beta \in [0,1)$ should be large (close to 1), which comports with empirical findings. We also provide experimental findings that further validate these conclusions.

Understanding How Over-Parametrization Leads to Acceleration: A case of learning a single teacher neuron

Over-parametrization has become a popular technique in deep learning. It is observed that by over-parametrization, a larger neural network needs a fewer training iterations than a smaller one to achieve a certain level of performance -- namely, over-parametrization leads to acceleration in optimization. However, despite that over-parametrization is widely used nowadays, little theory is available to explain the acceleration due to over-parametrization. In this paper, we propose understanding it by studying a simple problem first. Specifically, we consider the setting that there is a single teacher neuron with quadratic activation, where over-parametrization is realized by having multiple student neurons learn the data generated from the teacher neuron. We provably show that over-parametrization helps the iterate generated by gradient descent to enter the neighborhood of a global optimal solution that achieves zero testing error faster. On the other hand, we also point out an issue regarding the necessity of over-parametrization and study how the scaling of the output neurons affects the convergence time.

Provable Acceleration of Neural Net Training via Polyak's Momentum

Incorporating a so-called "momentum" dynamic in gradient descent methods is widely used in neural net training as it has been broadly observed that, at least empirically, it often leads to significantly faster convergence. At the same time, there are very few theoretical guarantees in the literature to explain this apparent acceleration effect. In this paper we show that Polyak's momentum, in combination with over-parameterization of the model, helps achieve faster convergence in training a one-layer ReLU network on $n$ examples. We show specifically that gradient descent with Polyak's momentum decreases the initial training error at a rate much faster than that of vanilla gradient descent. We provide a bound for a fixed sample size $n$, and we show that gradient descent with Polyak's momentum converges at an accelerated rate to a small error that is controllable by the number of neurons $m$. Prior work [DZPS19] showed that using vanilla gradient descent, and with a similar method of over-parameterization, the error decays as $(1-\kappa_n)^t$ after $t$ iterations, where $\kappa_n$ is a problem-specific parameter. Our result shows that with the appropriate choice of parameters one has a rate of $(1-\sqrt{\kappa_n})^t$. This work establishes that momentum does indeed speed up neural net training.