Translation-Equivariance of Normalization Layers and Aliasing in Convolutional Neural Networks

The design of convolutional neural architectures that are exactly equivariant to continuous translations is an active field of research. It promises to benefit scientific computing, notably by making existing imaging systems more physically accurate. Most efforts focus on the design of downsampling/pooling layers, upsampling layers and activation functions, but little attention is dedicated to normalization layers. In this work, we present a novel theoretical framework for understanding the equivariance of normalization layers to discrete shifts and continuous translations. We also determine necessary and sufficient conditions for normalization layers to be equivariant in terms of the dimensions they operate on. Using real feature maps from ResNet-18 and ImageNet, we test those theoretical results empirically and find that they are consistent with our predictions.

DeepInverse: A Python package for solving imaging inverse problems with deep learning

DeepInverse is an open-source PyTorch-based library for solving imaging inverse problems. The library covers all crucial steps in image reconstruction from the efficient implementation of forward operators (e.g., optics, MRI, tomography), to the definition and resolution of variational problems and the design and training of advanced neural network architectures. In this paper, we describe the main functionality of the library and discuss the main design choices.

Generalized Recorrupted-to-Recorrupted: Self-Supervised Learning Beyond Gaussian Noise

Recorrupted-to-Recorrupted (R2R) has emerged as a methodology for training deep networks for image restoration in a self-supervised manner from noisy measurement data alone, demonstrating equivalence in expectation to the supervised squared loss in the case of Gaussian noise. However, its effectiveness with non-Gaussian noise remains unexplored. In this paper, we propose Generalized R2R (GR2R), extending the R2R framework to handle a broader class of noise distribution as additive noise like log-Rayleigh and address the natural exponential family including Poisson and Gamma noise distributions, which play a key role in many applications including low-photon imaging and synthetic aperture radar. We show that the GR2R loss is an unbiased estimator of the supervised loss and that the popular Stein's unbiased risk estimator can be seen as a special case. A series of experiments with Gaussian, Poisson, and Gamma noise validate GR2R's performance, showing its effectiveness compared to other self-supervised methods.

UNSURE: Unknown Noise level Stein's Unbiased Risk Estimator

Recently, many self-supervised learning methods for image reconstruction have been proposed that can learn from noisy data alone, bypassing the need for ground-truth references. Most existing methods cluster around two classes: i) Noise2Self and similar cross-validation methods that require very mild knowledge about the noise distribution, and ii) Stein's Unbiased Risk Estimator (SURE) and similar approaches that assume full knowledge of the distribution. The first class of methods is often suboptimal compared to supervised learning, and the second class is often impractical, as the noise level is generally unknown in real-world applications. In this paper, we provide a theoretical framework that characterizes this expressivity-robustness trade-off and propose a new approach based on SURE, but unlike the standard SURE, does not require knowledge about the noise level. Throughout a series of experiments, we show that the proposed estimator outperforms other existing self-supervised methods on various imaging inverse problems.

Self-Supervised Learning for Image Super-Resolution and Deblurring

Self-supervised methods have recently proved to be nearly as effective as supervised methods in various imaging inverse problems, paving the way for learning-based methods in scientific and medical imaging applications where ground truth data is hard or expensive to obtain. This is the case in magnetic resonance imaging and computed tomography. These methods critically rely on invariance to translations and/or rotations of the image distribution to learn from incomplete measurement data alone. However, existing approaches fail to obtain competitive performances in the problems of image super-resolution and deblurring, which play a key role in most imaging systems. In this work, we show that invariance to translations and rotations is insufficient to learn from measurements that only contain low-frequency information. Instead, we propose a new self-supervised approach that leverages the fact that many image distributions are approximately scale-invariant, and that can be applied to any inverse problem where high-frequency information is lost in the measurement process. We demonstrate throughout a series of experiments on real datasets that the proposed method outperforms other self-supervised approaches, and obtains performances on par with fully supervised learning.

Learning to Reconstruct Signals From Binary Measurements

Recent advances in unsupervised learning have highlighted the possibility of learning to reconstruct signals from noisy and incomplete linear measurements alone. These methods play a key role in medical and scientific imaging and sensing, where ground truth data is often scarce or difficult to obtain. However, in practice, measurements are not only noisy and incomplete but also quantized. Here we explore the extreme case of learning from binary observations and provide necessary and sufficient conditions on the number of measurements required for identifying a set of signals from incomplete binary data. Our results are complementary to existing bounds on signal recovery from binary measurements. Furthermore, we introduce a novel self-supervised learning approach, which we name SSBM, that only requires binary data for training. We demonstrate in a series of experiments with real datasets that SSBM performs on par with supervised learning and outperforms sparse reconstruction methods with a fixed wavelet basis by a large margin.

Imaging with Equivariant Deep Learning

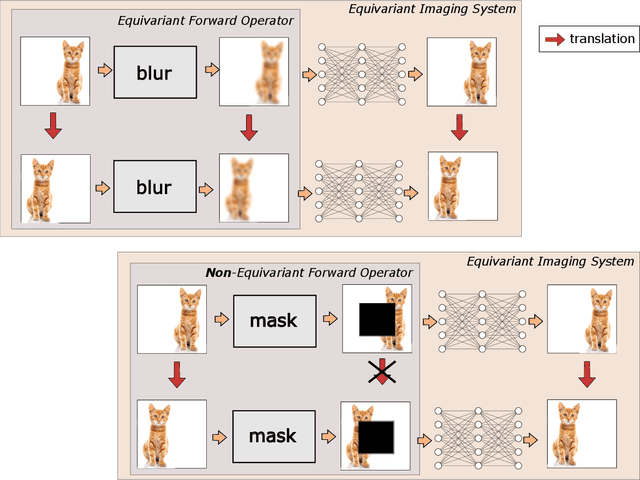
From early image processing to modern computational imaging, successful models and algorithms have relied on a fundamental property of natural signals: symmetry. Here symmetry refers to the invariance property of signal sets to transformations such as translation, rotation or scaling. Symmetry can also be incorporated into deep neural networks in the form of equivariance, allowing for more data-efficient learning. While there has been important advances in the design of end-to-end equivariant networks for image classification in recent years, computational imaging introduces unique challenges for equivariant network solutions since we typically only observe the image through some noisy ill-conditioned forward operator that itself may not be equivariant. We review the emerging field of equivariant imaging and show how it can provide improved generalization and new imaging opportunities. Along the way we show the interplay between the acquisition physics and group actions and links to iterative reconstruction, blind compressed sensing and self-supervised learning.

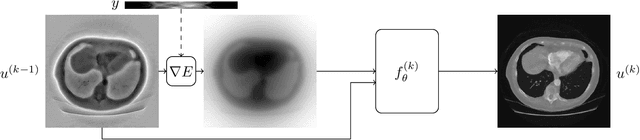
Sampling Theorems for Unsupervised Learning in Linear Inverse Problems

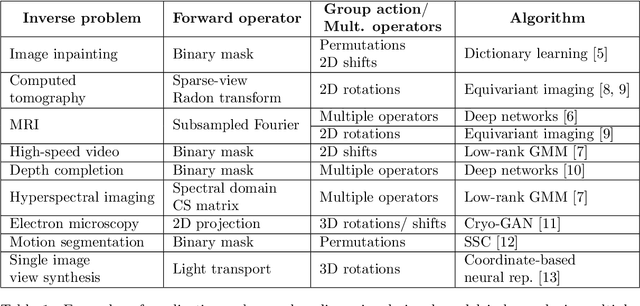
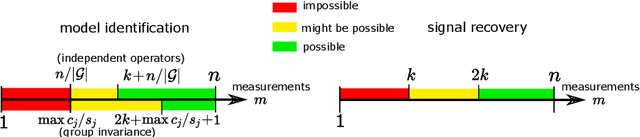
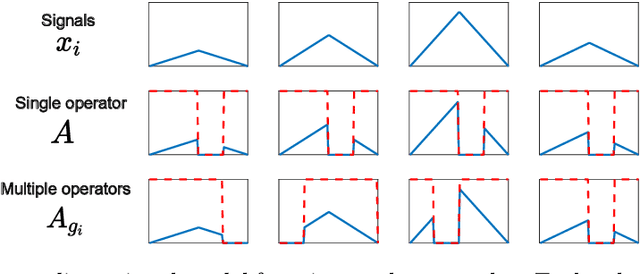
Solving a linear inverse problem requires knowledge about the underlying signal model. In many applications, this model is a priori unknown and has to be learned from data. However, it is impossible to learn the model using observations obtained via a single incomplete measurement operator, as there is no information outside the range of the inverse operator, resulting in a chicken-and-egg problem: to learn the model we need reconstructed signals, but to reconstruct the signals we need to know the model. Two ways to overcome this limitation are using multiple measurement operators or assuming that the signal model is invariant to a certain group action. In this paper, we present necessary and sufficient sampling conditions for learning the signal model from partial measurements which only depend on the dimension of the model, and the number of operators or properties of the group action that the model is invariant to. As our results are agnostic of the learning algorithm, they shed light into the fundamental limitations of learning from incomplete data and have implications in a wide range set of practical algorithms, such as dictionary learning, matrix completion and deep neural networks.

Sketched RT3D: How to reconstruct billions of photons per second

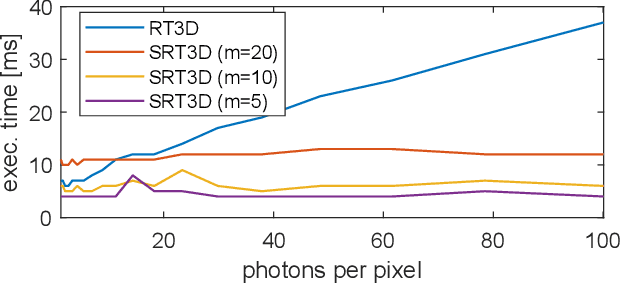
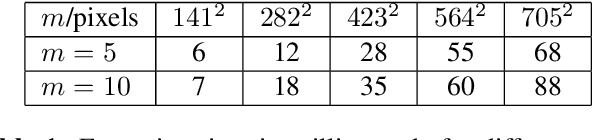
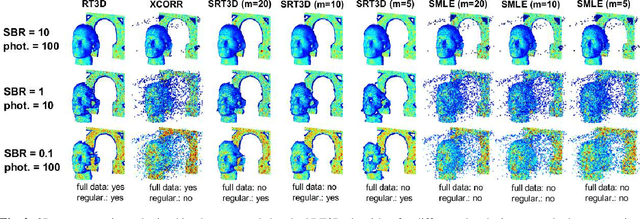
Single-photon light detection and ranging (lidar) captures depth and intensity information of a 3D scene. Reconstructing a scene from observed photons is a challenging task due to spurious detections associated with background illumination sources. To tackle this problem, there is a plethora of 3D reconstruction algorithms which exploit spatial regularity of natural scenes to provide stable reconstructions. However, most existing algorithms have computational and memory complexity proportional to the number of recorded photons. This complexity hinders their real-time deployment on modern lidar arrays which acquire billions of photons per second. Leveraging a recent lidar sketching framework, we show that it is possible to modify existing reconstruction algorithms such that they only require a small sketch of the photon information. In particular, we propose a sketched version of a recent state-of-the-art algorithm which uses point cloud denoisers to provide spatially regularized reconstructions. A series of experiments performed on real lidar datasets demonstrates a significant reduction of execution time and memory requirements, while achieving the same reconstruction performance than in the full data case.

Sampling Theorems for Learning from Incomplete Measurements

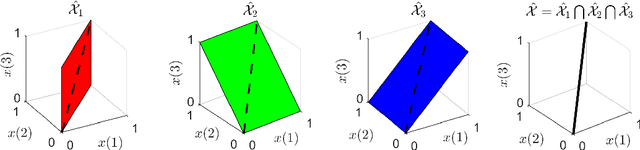
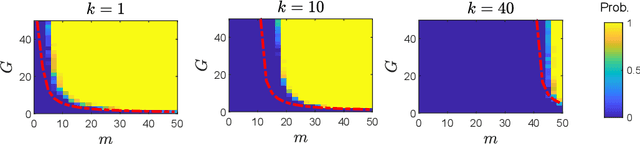
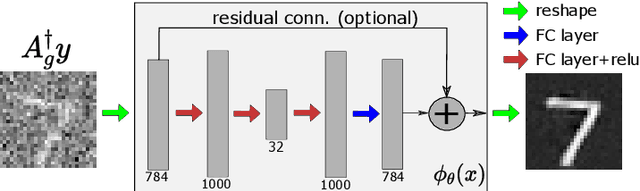
In many real-world settings, only incomplete measurement data are available which can pose a problem for learning. Unsupervised learning of the signal model using a fixed incomplete measurement process is impossible in general, as there is no information in the nullspace of the measurement operator. This limitation can be overcome by using measurements from multiple operators. While this idea has been successfully applied in various applications, a precise characterization of the conditions for learning is still lacking. In this paper, we fill this gap by presenting necessary and sufficient conditions for learning the signal model which indicate the interplay between the number of distinct measurement operators $G$, the number of measurements per operator $m$, the dimension of the model $k$ and the dimension of the signals $n$. In particular, we show that generically unsupervised learning is possible if each operator obtains at least $m>k+n/G$ measurements. Our results are agnostic of the learning algorithm and have implications in a wide range of practical algorithms, from low-rank matrix recovery to deep neural networks.