Associations among Image Assessments as Cost Functions in Linear Decomposition: MSE, SSIM, and Correlation Coefficient

The traditional methods of image assessment, such as mean squared error (MSE), signal-to-noise ratio (SNR), and Peak signal-to-noise ratio (PSNR), are all based on the absolute error of images. Pearson's inner-product correlation coefficient (PCC) is also usually used to measure the similarity between images. Structural similarity (SSIM) index is another important measurement which has been shown to be more effective in the human vision system (HVS). Although there are many essential differences among these image assessments, some important associations among them as cost functions in linear decomposition are discussed in this paper. Firstly, the selected bases from a basis set for a target vector are the same in the linear decomposition schemes with different cost functions MSE, SSIM, and PCC. Moreover, for a target vector, the ratio of the corresponding affine parameters in the MSE-based linear decomposition scheme and the SSIM-based scheme is a constant, which is just the value of PCC between the target vector and its estimated vector.

Kernel Risk-Sensitive Loss: Definition, Properties and Application to Robust Adaptive Filtering

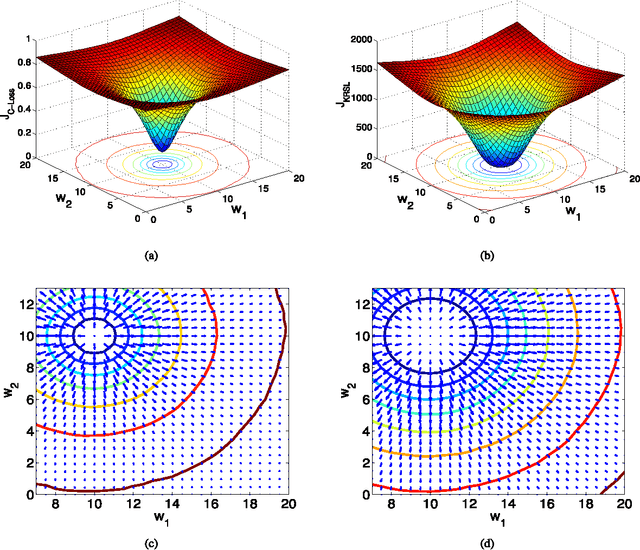
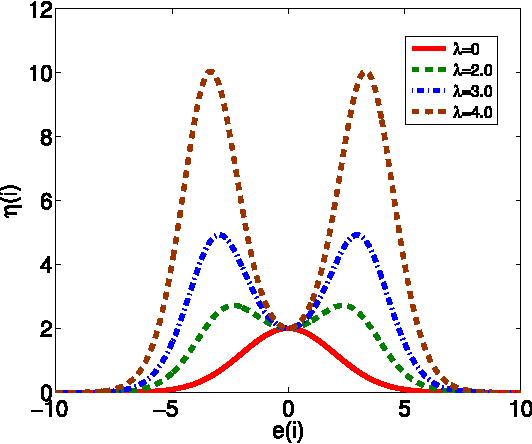
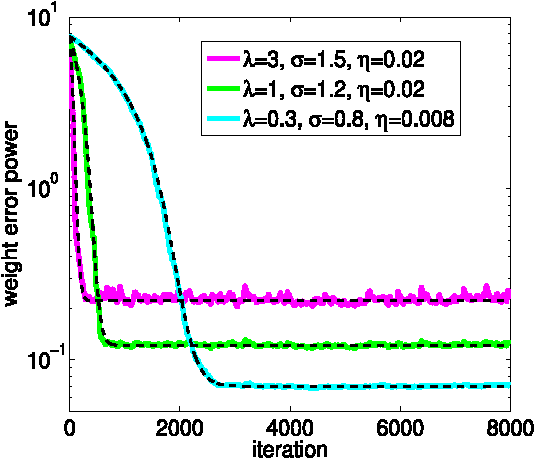
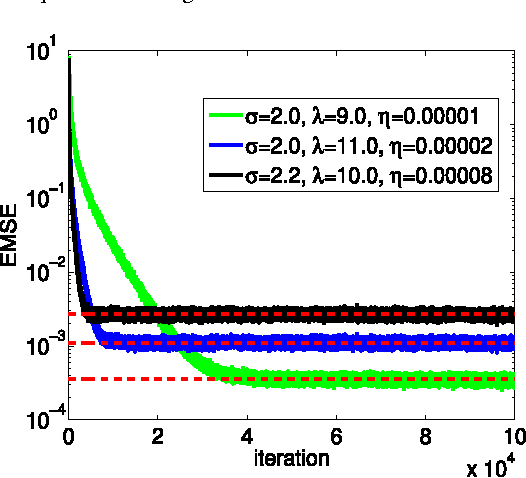
Nonlinear similarity measures defined in kernel space, such as correntropy, can extract higher-order statistics of data and offer potentially significant performance improvement over their linear counterparts especially in non-Gaussian signal processing and machine learning. In this work, we propose a new similarity measure in kernel space, called the kernel risk-sensitive loss (KRSL), and provide some important properties. We apply the KRSL to adaptive filtering and investigate the robustness, and then develop the MKRSL algorithm and analyze the mean square convergence performance. Compared with correntropy, the KRSL can offer a more efficient performance surface, thereby enabling a gradient based method to achieve faster convergence speed and higher accuracy while still maintaining the robustness to outliers. Theoretical analysis results and superior performance of the new algorithm are confirmed by simulation.

Computational Intelligence Challenges and Applications on Large-Scale Astronomical Time Series Databases

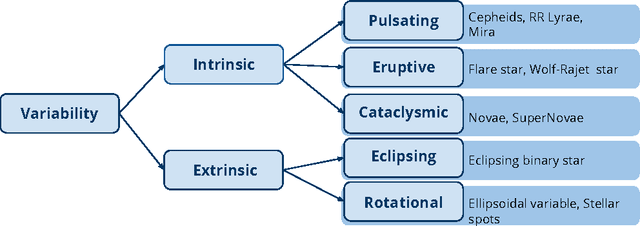
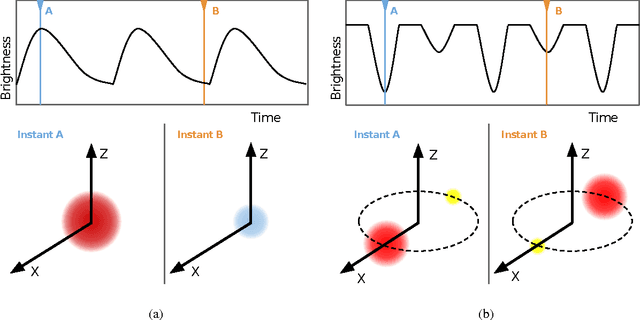
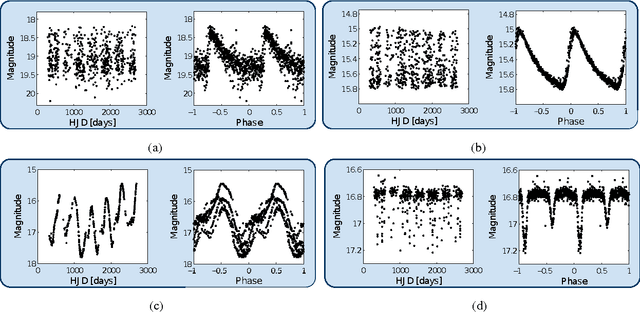
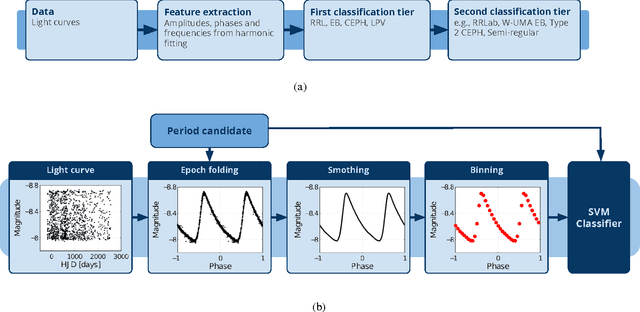
Time-domain astronomy (TDA) is facing a paradigm shift caused by the exponential growth of the sample size, data complexity and data generation rates of new astronomical sky surveys. For example, the Large Synoptic Survey Telescope (LSST), which will begin operations in northern Chile in 2022, will generate a nearly 150 Petabyte imaging dataset of the southern hemisphere sky. The LSST will stream data at rates of 2 Terabytes per hour, effectively capturing an unprecedented movie of the sky. The LSST is expected not only to improve our understanding of time-varying astrophysical objects, but also to reveal a plethora of yet unknown faint and fast-varying phenomena. To cope with a change of paradigm to data-driven astronomy, the fields of astroinformatics and astrostatistics have been created recently. The new data-oriented paradigms for astronomy combine statistics, data mining, knowledge discovery, machine learning and computational intelligence, in order to provide the automated and robust methods needed for the rapid detection and classification of known astrophysical objects as well as the unsupervised characterization of novel phenomena. In this article we present an overview of machine learning and computational intelligence applications to TDA. Future big data challenges and new lines of research in TDA, focusing on the LSST, are identified and discussed from the viewpoint of computational intelligence/machine learning. Interdisciplinary collaboration will be required to cope with the challenges posed by the deluge of astronomical data coming from the LSST.

Measures of Entropy from Data Using Infinitely Divisible Kernels

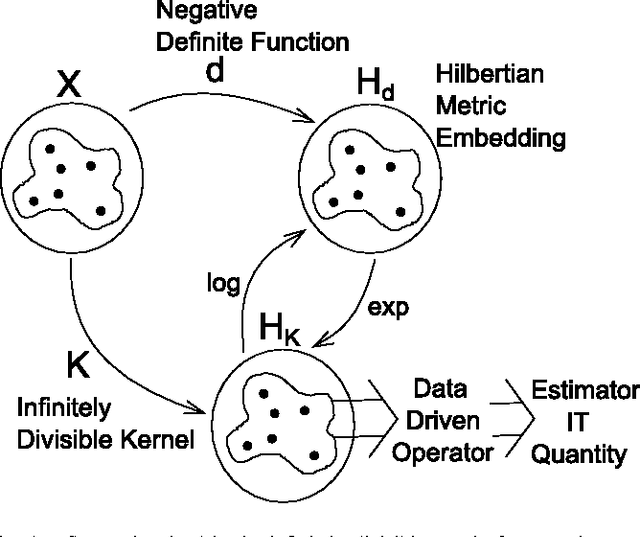
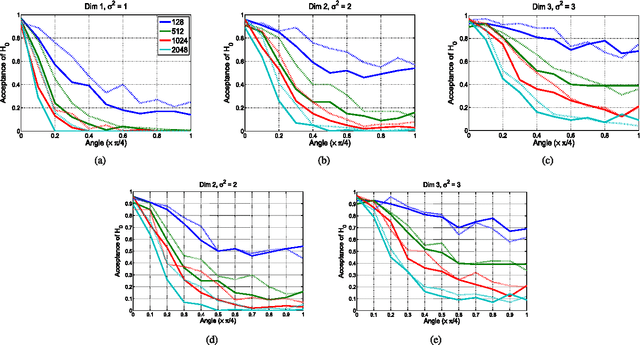
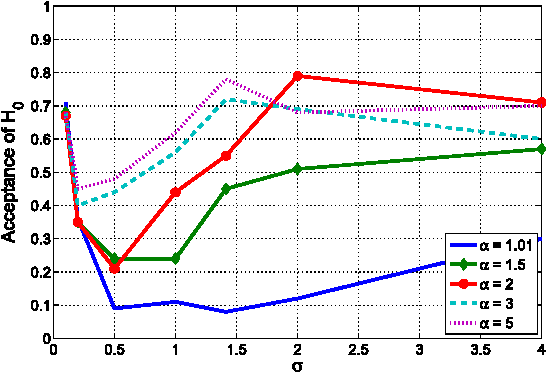
Information theory provides principled ways to analyze different inference and learning problems such as hypothesis testing, clustering, dimensionality reduction, classification, among others. However, the use of information theoretic quantities as test statistics, that is, as quantities obtained from empirical data, poses a challenging estimation problem that often leads to strong simplifications such as Gaussian models, or the use of plug in density estimators that are restricted to certain representation of the data. In this paper, a framework to non-parametrically obtain measures of entropy directly from data using operators in reproducing kernel Hilbert spaces defined by infinitely divisible kernels is presented. The entropy functionals, which bear resemblance with quantum entropies, are defined on positive definite matrices and satisfy similar axioms to those of Renyi's definition of entropy. Convergence of the proposed estimators follows from concentration results on the difference between the ordered spectrum of the Gram matrices and the integral operators associated to the population quantities. In this way, capitalizing on both the axiomatic definition of entropy and on the representation power of positive definite kernels, the proposed measure of entropy avoids the estimation of the probability distribution underlying the data. Moreover, estimators of kernel-based conditional entropy and mutual information are also defined. Numerical experiments on independence tests compare favourably with state of the art.

Rate-Distortion Auto-Encoders

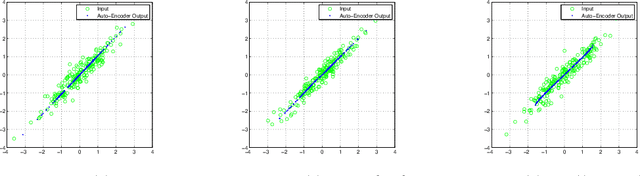
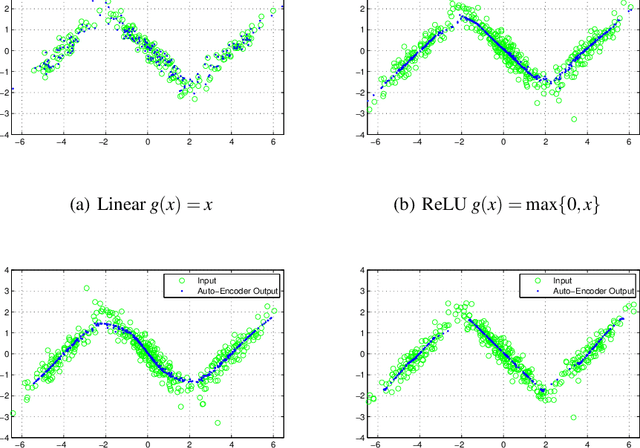
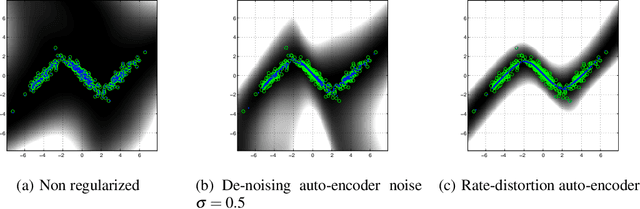
A rekindled the interest in auto-encoder algorithms has been spurred by recent work on deep learning. Current efforts have been directed towards effective training of auto-encoder architectures with a large number of coding units. Here, we propose a learning algorithm for auto-encoders based on a rate-distortion objective that minimizes the mutual information between the inputs and the outputs of the auto-encoder subject to a fidelity constraint. The goal is to learn a representation that is minimally committed to the input data, but that is rich enough to reconstruct the inputs up to certain level of distortion. Minimizing the mutual information acts as a regularization term whereas the fidelity constraint can be understood as a risk functional in the conventional statistical learning setting. The proposed algorithm uses a recently introduced measure of entropy based on infinitely divisible matrices that avoids the plug in estimation of densities. Experiments using over-complete bases show that the rate-distortion auto-encoders can learn a regularized input-output mapping in an implicit manner.

Kernel Least Mean Square with Adaptive Kernel Size

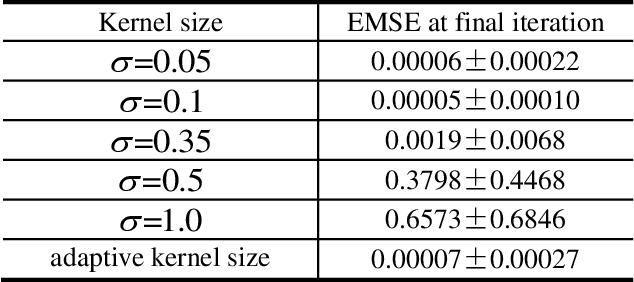
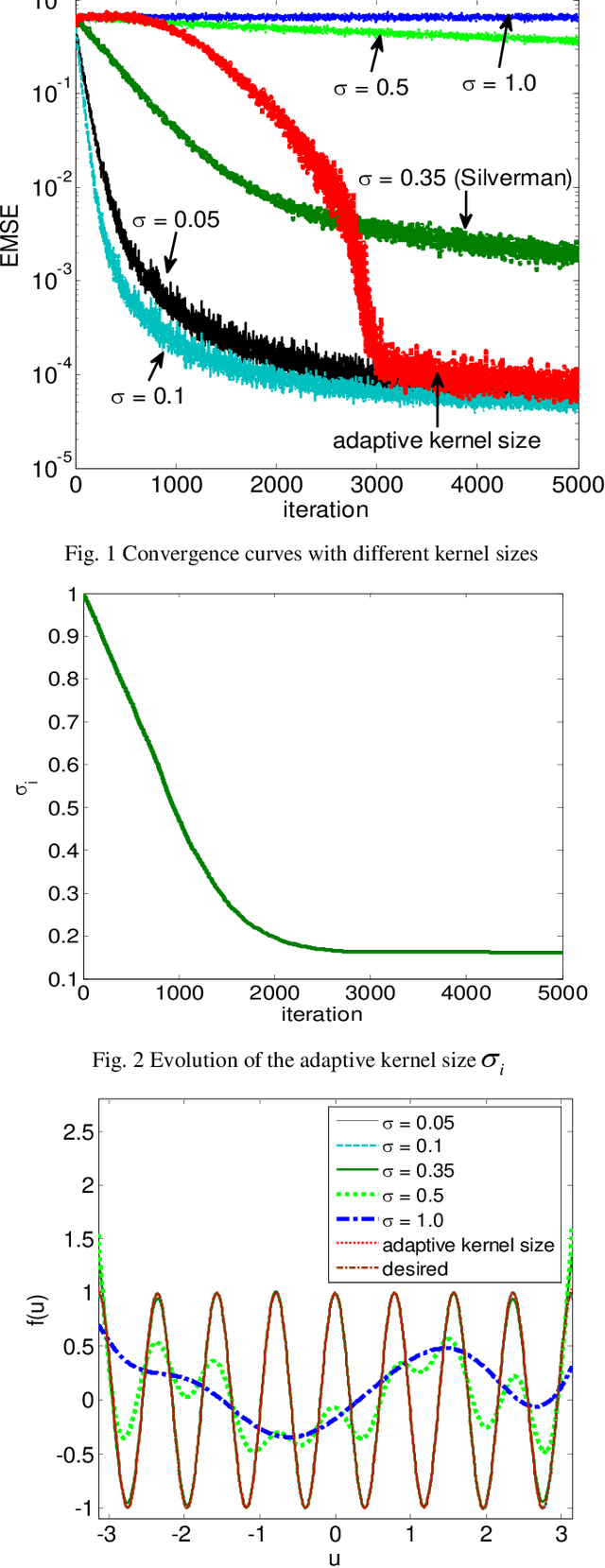
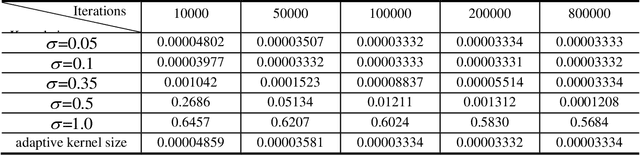
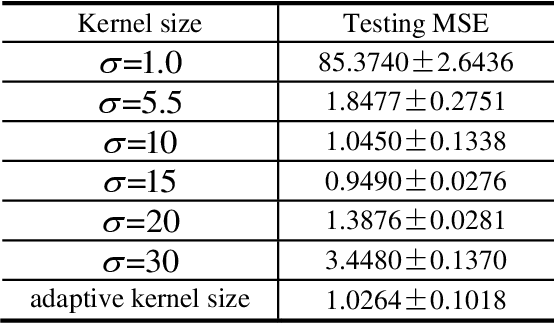
Kernel adaptive filters (KAF) are a class of powerful nonlinear filters developed in Reproducing Kernel Hilbert Space (RKHS). The Gaussian kernel is usually the default kernel in KAF algorithms, but selecting the proper kernel size (bandwidth) is still an open important issue especially for learning with small sample sizes. In previous research, the kernel size was set manually or estimated in advance by Silvermans rule based on the sample distribution. This study aims to develop an online technique for optimizing the kernel size of the kernel least mean square (KLMS) algorithm. A sequential optimization strategy is proposed, and a new algorithm is developed, in which the filter weights and the kernel size are both sequentially updated by stochastic gradient algorithms that minimize the mean square error (MSE). Theoretical results on convergence are also presented. The excellent performance of the new algorithm is confirmed by simulations on static function estimation and short term chaotic time series prediction.

Information Theoretic Learning with Infinitely Divisible Kernels

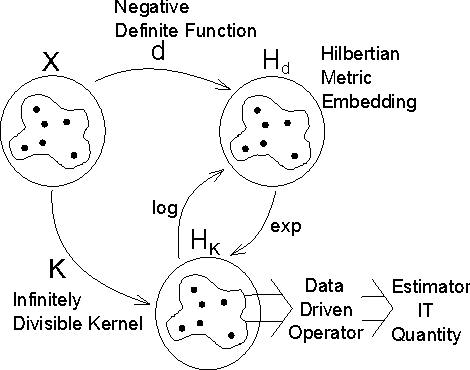
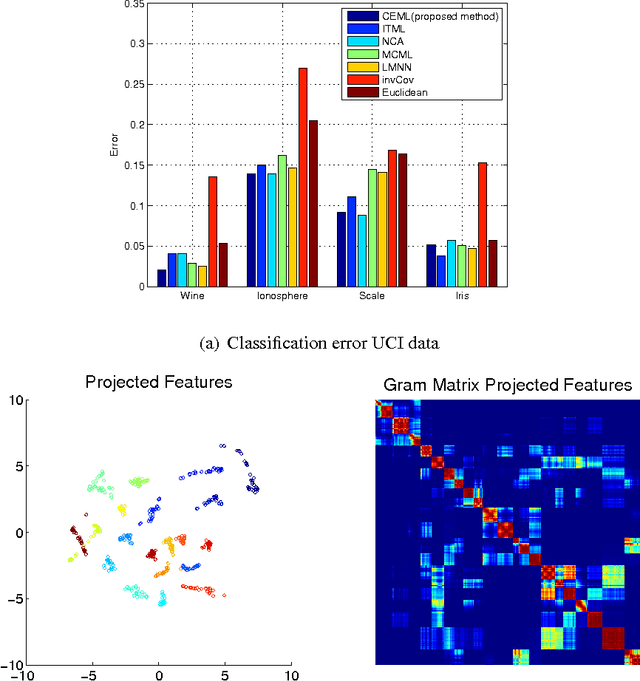
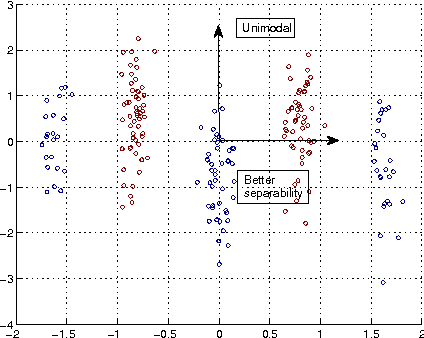
In this paper, we develop a framework for information theoretic learning based on infinitely divisible matrices. We formulate an entropy-like functional on positive definite matrices based on Renyi's axiomatic definition of entropy and examine some key properties of this functional that lead to the concept of infinite divisibility. The proposed formulation avoids the plug in estimation of density and brings along the representation power of reproducing kernel Hilbert spaces. As an application example, we derive a supervised metric learning algorithm using a matrix based analogue to conditional entropy achieving results comparable with the state of the art.

Deep Predictive Coding Networks

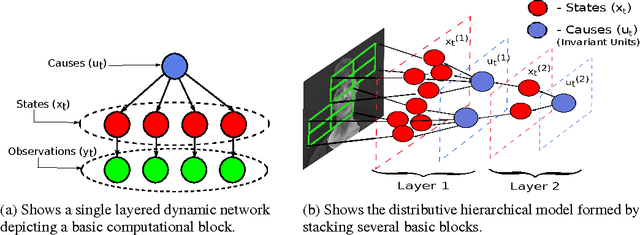
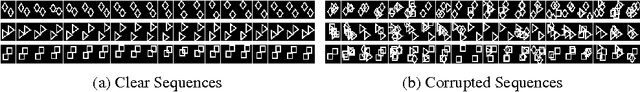
The quality of data representation in deep learning methods is directly related to the prior model imposed on the representations; however, generally used fixed priors are not capable of adjusting to the context in the data. To address this issue, we propose deep predictive coding networks, a hierarchical generative model that empirically alters priors on the latent representations in a dynamic and context-sensitive manner. This model captures the temporal dependencies in time-varying signals and uses top-down information to modulate the representation in lower layers. The centerpiece of our model is a novel procedure to infer sparse states of a dynamic model which is used for feature extraction. We also extend this feature extraction block to introduce a pooling function that captures locally invariant representations. When applied on a natural video data, we show that our method is able to learn high-level visual features. We also demonstrate the role of the top-down connections by showing the robustness of the proposed model to structured noise.