Positional versus Symbolic Attention Heads: Learning Dynamics, RoPE Geometry, and Length Generalization

Transformer-based language models are widespread in today's society. As such, understanding the mechanisms by which they solve structured tasks and predicting how they may behave in novel scenarios is of great importance for safe deployment. We study the learning dynamics of attention heads in a controlled setting by training a decoder-only Transformer (GPT-J) on two structurally equivalent multi-hop reasoning tasks: a number task requiring positional reasoning and a letter task requiring symbolic reasoning. Using a recently introduced metric that classifies attention-head behavior as positional or symbolic for a given prompt, we show that successful learning is associated with the emergence of pure heads, i.e., heads that express themselves as either positional or symbolic. Despite the tasks' structural equivalence, they impose different mechanistic demands: the number task requires both positional and symbolic heads, whereas the letter task requires only symbolic heads. We then identify the computational roles of these heads, characterize the basic functions they implement, and give theoretical constructions showing how single-layer RoPE-based attention can realize these functions through geometrically interpretable query, key, and value operations. This analysis yields a quantitative separation between positional and symbolic mechanisms in their robustness to longer sequences, formalized through a novel notion of discrepancy. We empirically validate the resulting predictions in both controlled and real-world models, showing that symbolic mechanisms extrapolate more reliably to longer sequences while positional mechanisms face sharper limitations.

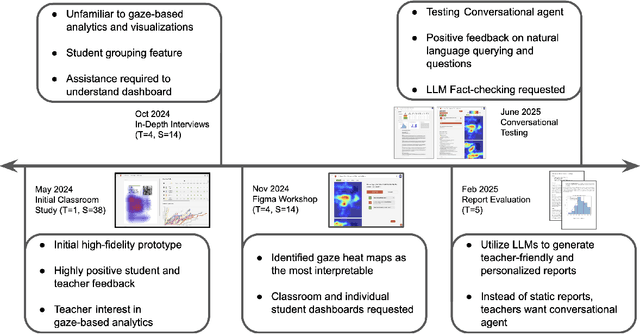
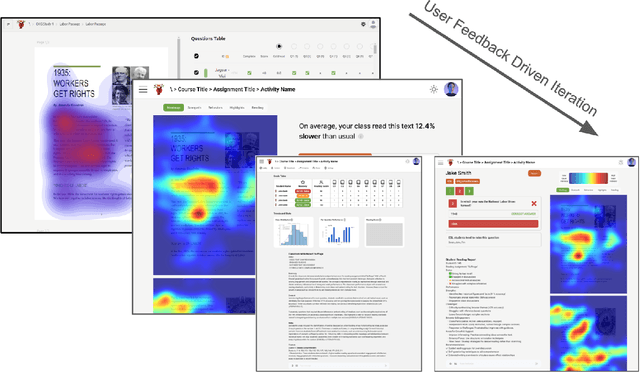
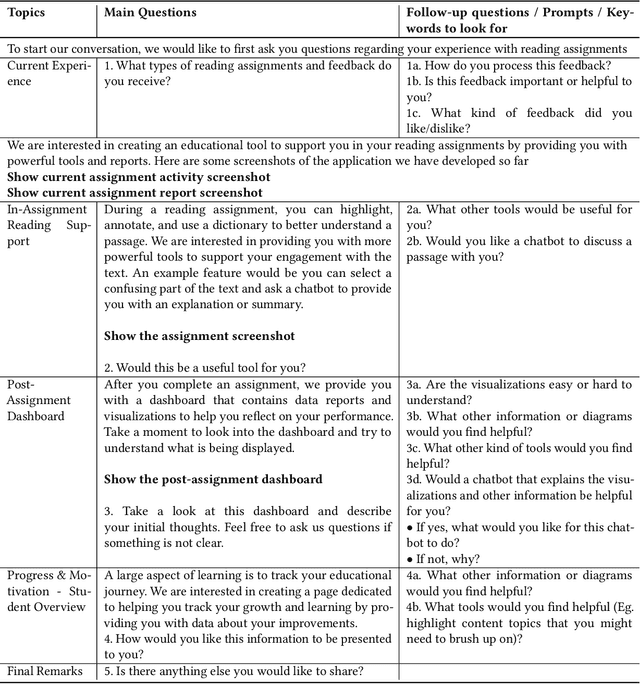
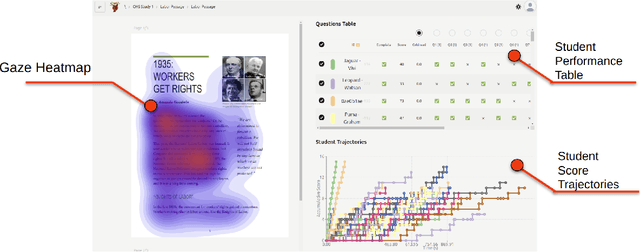
Designing Gaze Analytics for ELA Instruction: A User-Centered Dashboard with Conversational AI Support

Eye-tracking offers rich insights into student cognition and engagement, but remains underutilized in classroom-facing educational technology due to challenges in data interpretation and accessibility. In this paper, we present the iterative design and evaluation of a gaze-based learning analytics dashboard for English Language Arts (ELA), developed through five studies involving teachers and students. Guided by user-centered design and data storytelling principles, we explored how gaze data can support reflection, formative assessment, and instructional decision-making. Our findings demonstrate that gaze analytics can be approachable and pedagogically valuable when supported by familiar visualizations, layered explanations, and narrative scaffolds. We further show how a conversational agent, powered by a large language model (LLM), can lower cognitive barriers to interpreting gaze data by enabling natural language interactions with multimodal learning analytics. We conclude with design implications for future EdTech systems that aim to integrate novel data modalities in classroom contexts.

Absolute Expressiveness of Subgraph Motif Centrality Measures

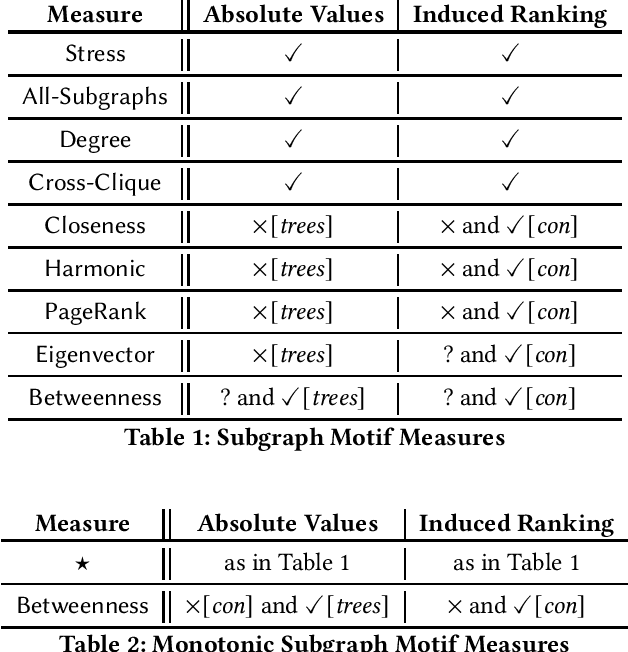
In graph-based applications, a common task is to pinpoint the most important or ``central'' vertex in a (directed or undirected) graph, or rank the vertices of a graph according to their importance. To this end, a plethora of so-called centrality measures have been proposed in the literature that assess which vertices in a graph are the most important ones. Riveros and Salas, in an ICDT 2020 paper, proposed a family of centrality measures based on the following intuitive principle: the importance of a vertex in a graph is relative to the number of ``relevant'' connected subgraphs, known as subgraph motifs, surrounding it. We refer to the measures derived from the above principle as subgraph motif measures. It has been convincingly argued that subgraph motif measures are well-suited for graph database applications. Although the ICDT paper studied several favourable properties enjoyed by subgraph motif measures, their absolute expressiveness remains largely unexplored. The goal of this work is to precisely characterize the absolute expressiveness of the family of subgraph motif measures.